ARIMA模型在甲型肝炎時間分布特征及趨勢預測中的應用

朱佳佳，胡登利，呂 媛*

（1．湖南師范大學醫學院，湖南 長沙 410013；2．中國人民解放軍第163醫院，湖南 長沙 410003）

甲型病毒性肝炎（Hepatitis A），簡稱甲肝，是甲肝病毒（Hepatitis A virus，HAV）引起的，主要經糞-口途徑傳播的急性傳染病。甲肝在全球均有報道，但由于經濟衛生條件差異，各個國家和地區 的甲肝流行趨勢呈現明顯差異。研究表明，收入水平和清潔飲用水可及性越高的國家和地區，甲肝發病率較低[1]。全球每年新發HAV感染者約140萬人，我國各地每年均有病例報告，呈高度散發，暴發主要集中在學校等人群密集區域，西部地區省份發病率較高[2]。近年來我國甲肝發病率呈下降趨勢，但發病人數中兒童和青少年占有很大比例[3]。本研究將采用自回歸移動平均模型（autoregressive integrated moving average model，ARIMA）分析我國甲肝的時間分布特征并就發病趨勢進行預測，探討其在甲肝發病預測中的可行性。

1 資料與方法

1.1 一般資料

2004年1月～2017年12月全國各省甲肝月發病數監測數據，來源于“中國疾病預防控制信息系統”網絡報告系統。

1.2 方法

基于2004年1月～2016年12月全國甲肝月發病數建立ARIMA乘積季節模型，并用2017年發病數據進行驗證預測效果。統計分析采用SPSS 23.0。

ARIMA模型的建立過程主要分為以下幾步[4]：原始序列平穩化處理、模型的識別、模型的參數估計和模型的診斷。

2 結 果

2.1 全國甲肝發病變化趨勢

繪制2004年1月～2016年12月全國甲肝月發病數時間序列圖（見圖1），發現我國甲肝全年均有發病，但發病數逐年遞減。每年6月～10月是發病高峰期，呈現一定的季節性波動，周期為12個月。故甲肝發病序列并不是穩定的時間序列。

2.2 時間序列的平穩化處理

對原始序列進行一階普通差分和一階周期為12的季節性差分后，發現時序圖趨于平穩，且自相關系數函數圖（ACF）截尾，偏自相關函數圖（PACF）拖尾，說明此時的序列為平穩序列，符合ARIMA模型要求。

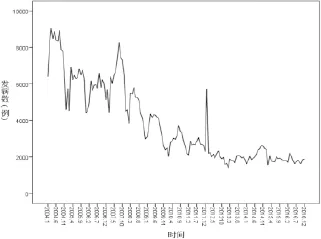
圖1 2004年～2016年全國甲肝月發病數時間序列圖

2.3 模型識別

由上述初步確定建立ARIMA（p，1，q）（P，1，Q）12模型，p，q和P，Q是連續模型和季節模型中的自回歸階數和移動平均階數，需依據平穩序列的ACF和PACF確定。相關文獻提示均不會超過2階，故采用由低階到高階方式擬合模型。經比較，ARIMA（0，1，1）（0，1，1）12模型的標準化BIC最小（12.954），且R2（0.884）和標準化R2（0.381）較高，擬合優度較高，因此可視為本研究的最優模型。

2.4 模型參數的估計與模型診斷

ARIMA（0，1，1）（0，1，1）12模型殘差的ACF和PACF均落在95%置信區間內（見圖2），提示殘差是隨機分布的。模型的參數估計結果見表1，差異均有統計學意義（P＜0.05）。Box-Ljung Q檢驗結果顯示殘差序列為白噪聲序列（P=0.907），說明模型對數據信息的提取較為充分。

表1 甲肝發病數最優ARIMA模型的參數估計

2.5 模型預測

ARIMA（0，1，1）（0，1，1）12模型對我國2017年1月～12月的甲肝發病的預測值和實際發病數比較結果見表2。所有預測值均落入95%置信區間內，二者基本吻合，預測值與實際值之間的相對誤差范圍為2.4%～37.1%，說明該模型對我國甲肝的實際發病有較好的的預測能力。

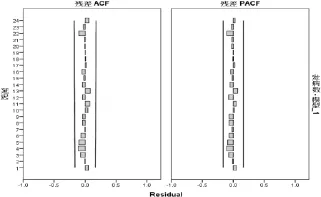
圖2 ARIMA（0，1，1）（0，1，1）12模型殘差序列的自相關系數圖和偏自相關系數圖

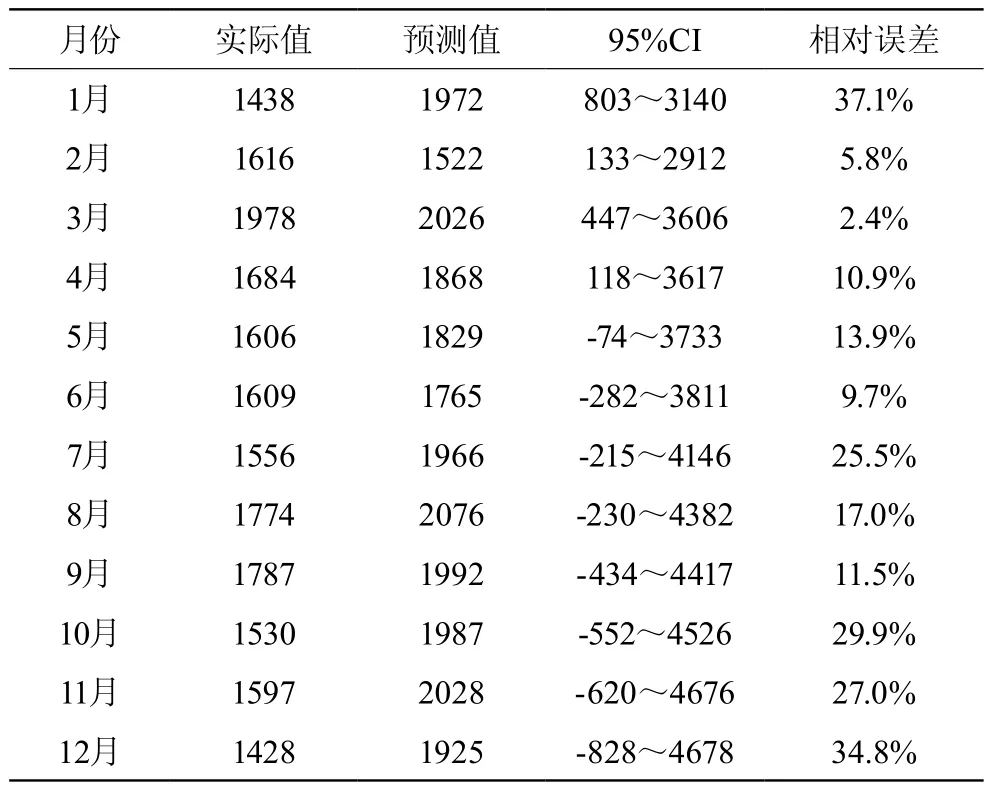
表2 2017年我國甲肝實際發病數與預測值比較

3 討 論

時間序列分析[4]能將影響疾病發生的多種因素綜合考慮于時間變量中，分析發病數據隨時間發展變化規律，并能進行有效外推預測[5]。ARIMA模型是時間序列分析最常用的方法之一，本文將ARIMA乘積季節模型應用于我國甲肝的發病規律研究中，利用2004年～2016年共156個月份的甲肝發病監測資料建立的ARIMA（0，1，1）（0，1，1）12模型，較好地反映了我國甲肝發病序列的特征。2017年1月～6月的驗證數據與實際值的吻合度較高，發病趨勢與往年基本一致，相對誤差較小，而7月～12月的預測數據相對誤差較大，表明利用ARIMA乘積季節模型可以對我國甲肝發病趨勢進行短期預測。

本研究的數據來源于我國傳染病報告信息系統，質量可靠，但應注意的是，ARIMA模型適合疾病的短期預測[6]，因此要不斷納入新的發病數據，調整模型參數以適應疾病的實際發生情況。此外，由于甲肝的發生還受諸多因素的影響，故后續研究中應嘗試將影響因素納入模型中以提高模型預測的精確性和準確性。