庫區深水高墩連續剛構橋抗震性能及減震措施分析

袁飛云,馬松華

(四川藏區高速公路有限責任公司,四川成都 610041)

連續剛構橋是一種常見的山區橋梁結構形式[1]，在地震荷載作用下，由于橋墩墩高差度較大導致其地震力傳遞不均勻；地震力的集中將導致結構整體抗震能力下降[2]。在跨越庫區時，或由于地質變動，橋墩可能沒入水中成為深水橋梁。動水壓力不利作用和非規則高墩使得深水橋梁易遭到地震破壞，而深水使得橋梁的維修加固難以進行[3、4]，岷江紫坪鋪水庫的深水連續剛構橋-廟子坪岷江特大橋就是典型的例子。

本文針對某深水高墩連續剛構橋，考慮動水壓力的影響，研究了其地震響應情況并對減震措施進行了探討，以期為該類橋梁抗震設計提供參考。

1 考慮動水壓力的地震響應分析

1.1 橋梁概況

該橋處于地震高烈度區，橋區地震設防烈度為8度(0.2g)，Ⅱ類場地，橋式方案采用抗震性能較好、方便懸臂施工的連續剛構橋。孔跨布置為25 m+62 m+ 112 m+62 m+25 m，總長286 m(圖1)。梁體為單箱雙室，寬度19.9 m，梁高度變化為5～9 m，頂板、底板及腹板厚度變化為0.5～0.8 m。小里程至大里程共布置4個橋墩(以下按里程大小分1～4#墩)，1#、4#為輔助墩，均為實心橢圓橋墩，1#高度為20 m，4#高度為12 m；2#、3#主墩均為矩形空心橋墩，2#墩高70 m，3#墩高55 m，墩頂橫橋向長度13.5 m，壁厚0.8 m，順橋向長度8 m，壁厚1 m，橫橋向外部、內部長度分別以橫向變坡1∶20、1∶40至墩底。

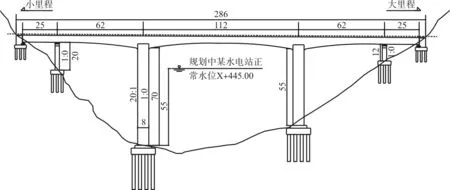
圖1 橋梁總布置

橋位即將修建水電站，修建完成后，正常蓄水時，2#墩將有55 m處于水中，3#墩將有40 m處于水中，動水壓力將給結構帶來一系列不利影響。同時，為了滿足峽谷地形，橋墩高度差別較大，非規則高墩將導致地震力分配不均勻。且梁體左右端均接入隧道，峽谷兩岸坡度較大且交通不便，河流水位高度變化大且不通航，橋梁施工期間現場交通是一大難點，而后期橋梁在線路運營期間發若生嚴重損壞，將難以修復。因此，此類橋梁的抗震設計就變得相當重要。

1.2 動水壓力計算在有限元分析中的實現

我國GB 50111-2006《鐵路工程抗震設計規范》中規定[5]，當水深高度超過5 m，應計入地震動水壓力對橋墩的影響。規范給出了普通梁式橋梁的動水壓力近似計算公式，但近似計算公式僅適用于跨度中等的橋梁，對大跨高墩深水墩-水相互作用仍缺少充分的研究。

墩水耦合過程十分復雜，為了方便有限元軟件計算，計算動水壓力時一般使用的方法為Morison方程[6]。Morison方程的前提條件是墩柱直徑比較小，對流場不產生影響，計算效率高，且在一定范圍內有足夠的精度。通過Morison方程將動水壓力轉化為橋墩節點附加質量可以大大減小工作量[7]。由于本文研究橋梁的橋墩長寬比較大，傳統的Morison方程并不適用，可以采取擴展Morison方程[8]。

對于空心矩形截面的橋墩，建立了考慮內水域影響的擴展Morison方程，其表達式為：

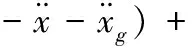
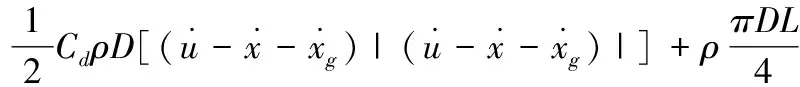
(1)

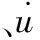
(2)

(3)

(4)

其中，D、D1分別為垂直矩形空心墩地震力方向對應的外、內截面邊長，L、L1為矩形空心地震方向外、內截面邊長。

根據截面尺寸，將計算的節段附加平動質量的一半分別加于節段上下對應的節點，兩種算法結果見圖2。其中，Mx為順橋向平動質量，My為橫橋向平動質量。

圖2可以看出，由于順橋向迎水面較大，計算的附加質量也就較大；隨著水深加大，附加質量也將變大。當結構的質量變大后，關鍵截面的地震響應將因此發生改變。

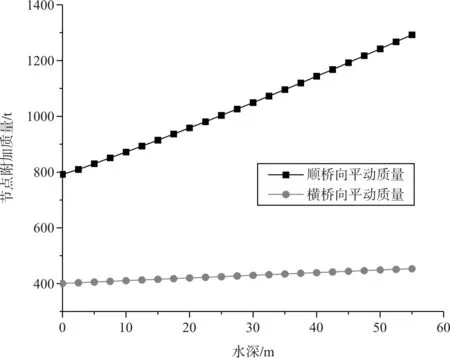
圖2 節點質量計算結果

1.3 考慮墩-水耦合作用的地震響應分析

為了探討動水壓力對結構地震響應的影響，需要對結構進行時程分析。本文選取人工擬合加速度地震波、El-Centro、Taft典型強震記錄加速度時程曲線作為激勵。三條曲線均為Ⅱ類場加速度波，經過調整，地震波加速度峰值為0.38g(罕遇地震)。三條地震加速度時程曲線下以及反應譜分析得到的結構關鍵部位的位移計算結果見表1。

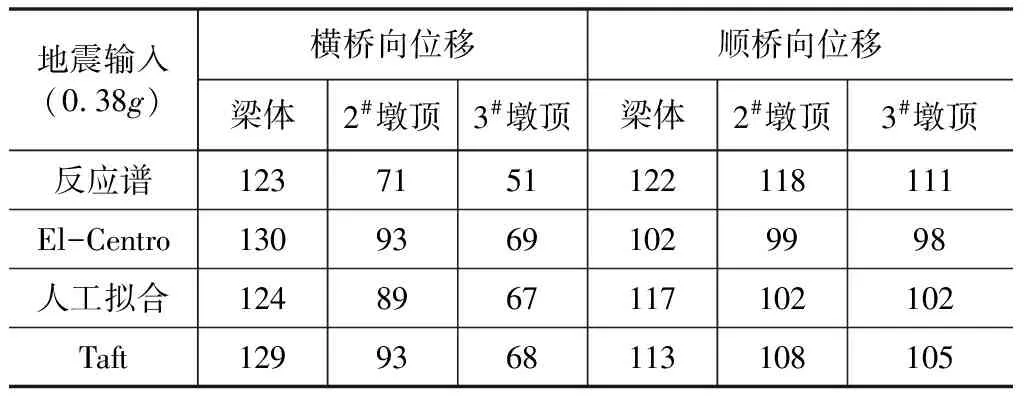
表1 橋梁關鍵部位最大位移對比 mm

1.4 動水壓力對結構的抗震影響

動水壓力的存在與否將影響結構的動力響應。下文以通用有限元軟件Midas計算有、無動水壓力下，探討橋梁的動力響應發生變化的規律。定義My為順橋向彎矩，Mz為橫橋向彎矩，計算結果見表2～表3。

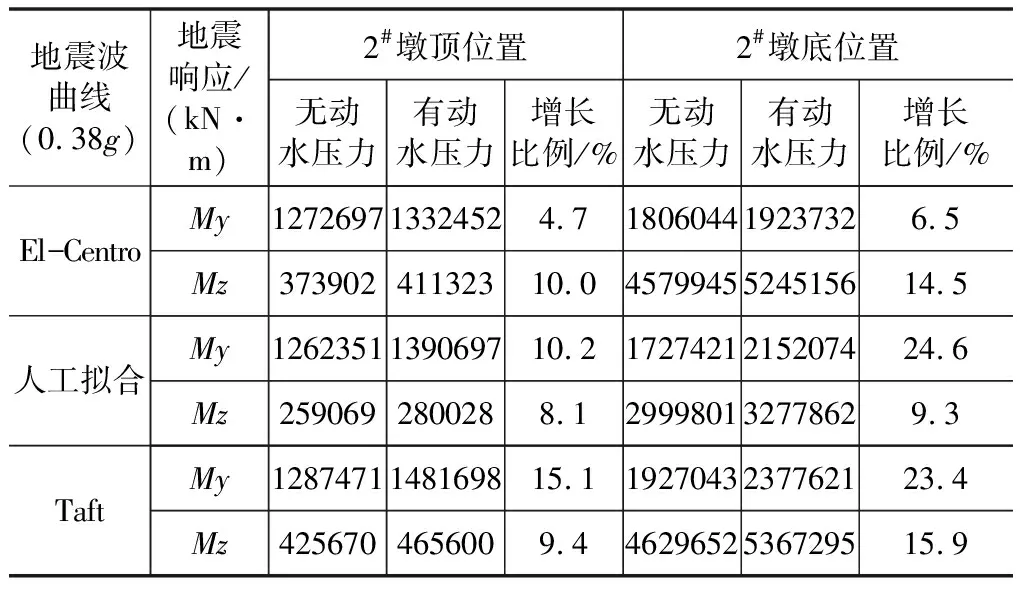
表2 2#主墩墩時程分析結果

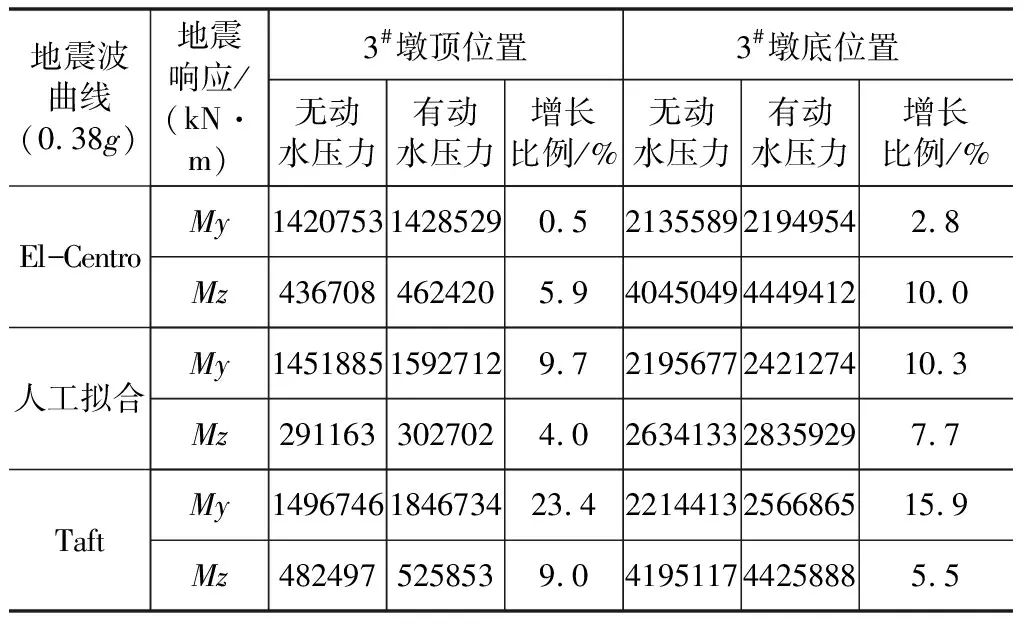
表3 3#主墩墩時程分析結果

從表2、表3可以得出以下結論：

(1)動水壓力對橋墩結構均起到不利作用，增大了關鍵截面處的地震響應值，增長比例最大能達到23.4 %，故在實際工程中需要引起注意。

(2)各條時程曲線計算結果存在差異，其中Taft地震波下，結構響應增長比例均較大，而El-Centro計算結果較小，這與地震波的頻譜特性有關系。

(3)由于縱向地震橋墩的迎水面較大，縱向彎矩增大幅度普遍大于橫向彎矩。

動水壓力導致地震響應增大，對于本文研究橋梁來說，由于橋墩橫向寬度大，縱向地震響應增大幅度更大，抗震設計中縱向地震效應往往較大。

2 墩高對地震響應的影響

規則的梁式橋梁結構比較對稱、橋墩高度差異不大，也因此地震力分配較均勻。而典型的山區橋梁，為了滿足地形需求，橋墩將設計為高度不一致的高墩。因此，主墩墩高差別較大、邊墩高度很矮，結構剛度差異較大；當梁墩的相對剛度及橋墩間的相關剛度較大時，地震效應將使得力更加集中于矮墩，導致矮墩比高墩先遭到破壞，高墩的承載力得不到利用[9]。

圖3給出了主墩墩頂位移時程圖，可以看出，橫向地震作用下，主墩橫向位移差別較小，地震力分配也較均勻；而縱向地震作用下下，3#矮墩位移明顯大于2#高墩，地震力集中于矮墩。由于地震力在縱橋向分配較均勻，主墩縱向地震作用下不出現塑性鉸[10]。圖4給出了主墩在橫向地震作用下塑性鉸分布位置圖，可以看出，3#矮墩墩頂、墩底塑性鉸長度均大于2#高墩，這是由于地震力集中導致的。而矮墩的承載力相對較小，這就使得橋梁抗震設計為橫向控制。

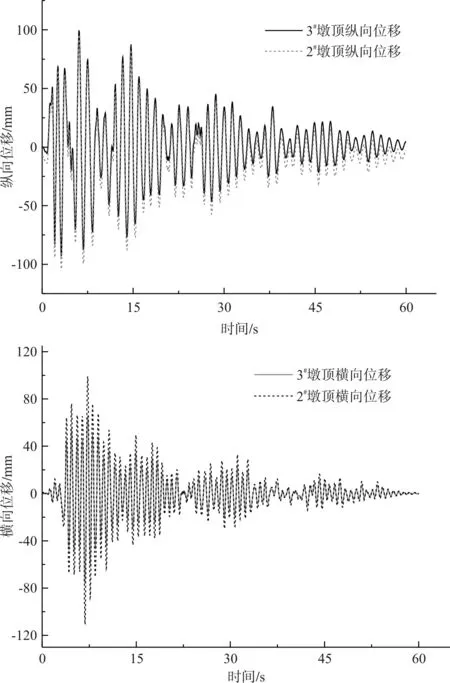
圖3 主墩墩頂位移對比

圖4 橫向地震作用下主墩塑性鉸分布

3 減震措施

通過設置減隔震設施，如阻尼器、隔震支座等，來減小地震力對結構的作用[11]。

本文采用MIDAS建立全橋模型，采用時程分析方法進行驗證，調整粘滯阻尼器的鎖定力在內的隔振參數，達到最佳抗震效果。粘滯阻尼器通過邊界非線性來模擬，采用MAXWELL模型，將阻尼單元與彈簧單元串聯進行計算，阻尼力F=CVα。其中，α為阻尼指數、C為阻尼系數、V為阻尼器端部運動速度[12]。模型中，在各個梁端模擬3個阻尼器，其阻尼指數分別為0.2、0.5、1.0，阻尼系數取值1 000～20 000 kN·(m/s)a。

各組阻尼參數下的兩題最大縱向位移分析結果析見圖5。圖5表明阻尼器對結構順橋向的減震效果較明顯，且減震效果與阻尼指數、阻尼系數有關。阻尼指數越小，消能效果越好，阻尼系數存在最優值，不同結構不同位置其值不一致。

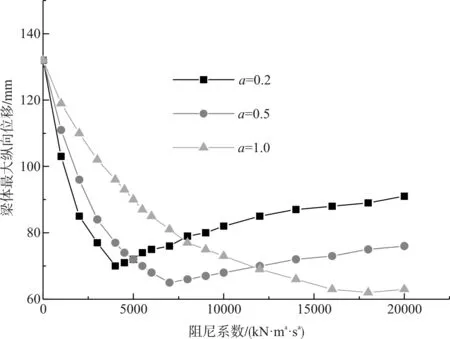
圖5 阻尼器參數分析結果(縱向位移)

由于且阻尼器價格與阻尼系數成正比，本橋阻尼器參數選定為：阻尼指數0.2，阻尼系數3 000 kN·(m/s)a，在梁端布置3個粘滯阻尼器并連接于橋臺，連接方向為縱向連接，即減震方向為縱向。減震前后3#墩頂位移對比見圖6，關鍵位置彎矩響應見表4。

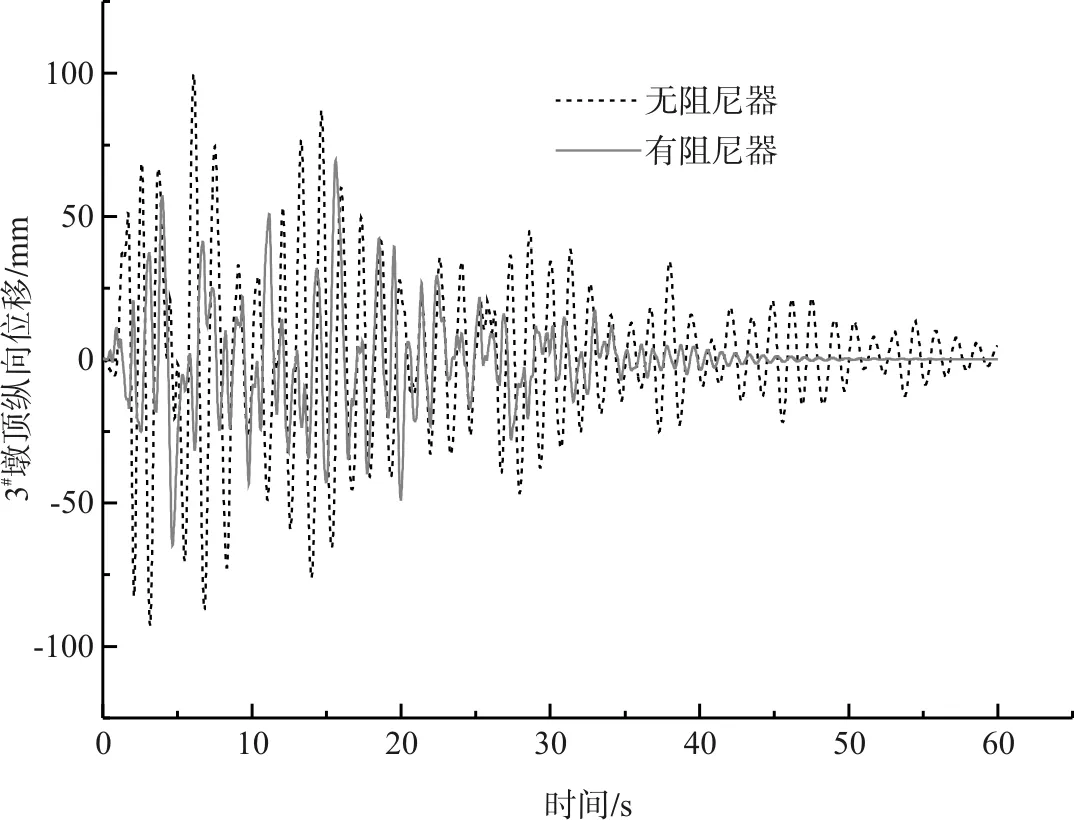
圖6 減震前后3#墩頂縱向位移時程(El波)

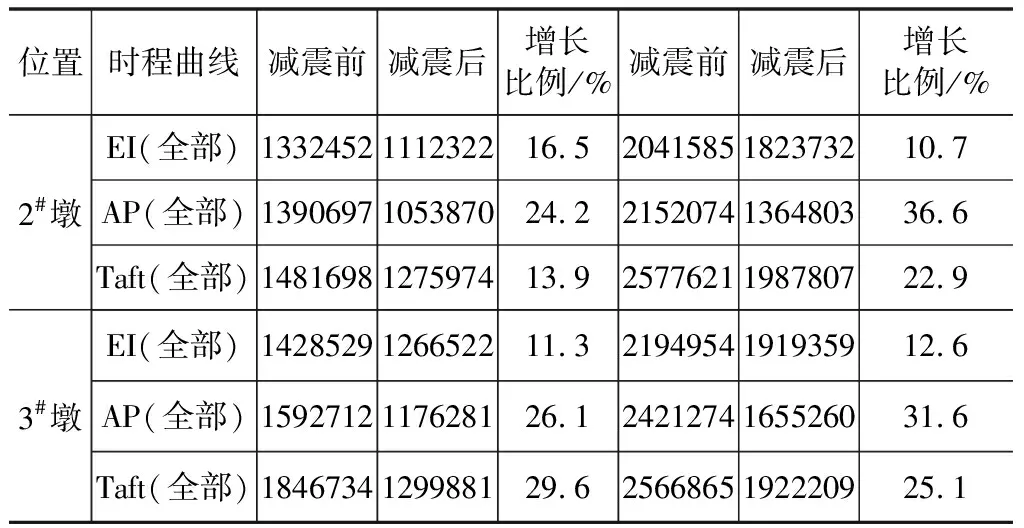
表4 減震前后橋底橫橋向彎矩響應對比 kN·m

圖6表明，阻尼器通過耗能，有效減小了墩頂的位移。表4可以看出，設置阻尼器后，結構的順橋向彎矩明顯降低，最多能降低36.6 %。順橋向地震作用下，整個結構不再出現塑形鉸，橋墩基本維持在彈性階段，結構的安全性大大增加。

4 結論

本文以某深水高墩三線鐵路連續剛構橋為例子，分析了動水壓力對結構抗震的不利影響，討論了三線鐵路橋梁非規則高墩對地震力分配的影響，并在結構抗震能力不足的情況下選定了阻尼器來減震。經過以上工作，得到以下幾個結論：

(1)動水壓力對深水橋梁的不利影響不可忽略。對于三線鐵路橋梁，由于橋墩橫向寬度較大，即縱向地震迎水面較大，從而導致動水壓力對縱向地震影響幅度更大。

(2)三線鐵路橋梁由于墩梁相對剛度較大，將導致地震力分配將發生改變：橫向地震力分配較均勻，這對結構是有利的，而縱向地震力分配將集中于承載力相對較低的矮墩，橋梁抗震設計往往為縱向控制。

(3)跨深水水庫橋梁由于維修加固困難，建議采取減震措施來提高抗震能力。對于本橋，選擇粘滯阻尼器最為減震措施，通過參數分析后，選定阻尼器的相關參數，計算表明：阻尼器對連續剛構橋的減震效果是十分明顯的。本橋通過在縱向設置阻尼器后，梁體縱向位移大大較小，主墩均不出現塑性鉸。