大跨度混凝土疊箱渡槽溫度梯度曲線研究

王力丹,劉 龍,張文學,黃 薦

(1.北京工業大學建筑工程學院，北京 100124；2.北京市道路工程質量監督站，北京 100076)

混凝土結構的熱傳導性能較差，長期經受自然界的大氣溫度和日輻射等劇烈作用，這種溫度荷載對工程結構的危害一直困擾著整個工程界,許多專家學者對此進行了大量的研究工作[1-4]。渡槽作為一種輸水結構，相比其他混凝土結構，對溫度荷載更為敏感，由此逐漸發展而成的貫穿裂縫將直接造成水資源的極大浪費。對于渡槽結構的研究，季日臣得出了太陽輻射下箱形渡槽溫度場變化特點及分布規律[5]；馮曉波在對南水北調中線大型渡槽的分析中給出了渡槽溫度場的邊界條件計算方法，為計算溫度應力奠定基礎[6]；李朝對放水河渡槽進行溫度場及溫度應力三維有限元分析后提出溫度裂縫的預防和控制措施[7]。

目前關于混凝土疊箱渡槽溫度場的研究相對較少，設計時多參照相關橋梁規范給出的溫度荷載模型。大跨度疊箱渡槽采用上下疊式箱形截面，與鐵路、公路箱梁截面相比，超靜定結構次數更多，將同時受到更大的自平衡溫度應力和外約束溫度應力，將橋梁溫度荷載模型直接用于疊箱渡槽是否合理有待于進一步驗證。鑒于此，筆者對黔中水利樞紐焦家渡槽的某典型截面溫度場分布情況進行研究，結合當地氣象條件，確定疊箱渡槽邊界條件和相關熱力學參數后，通過有限元模擬對疊箱渡槽、鐵路箱梁和公路箱梁的溫度梯度分布情況進行了對比分析。

1 工程概況

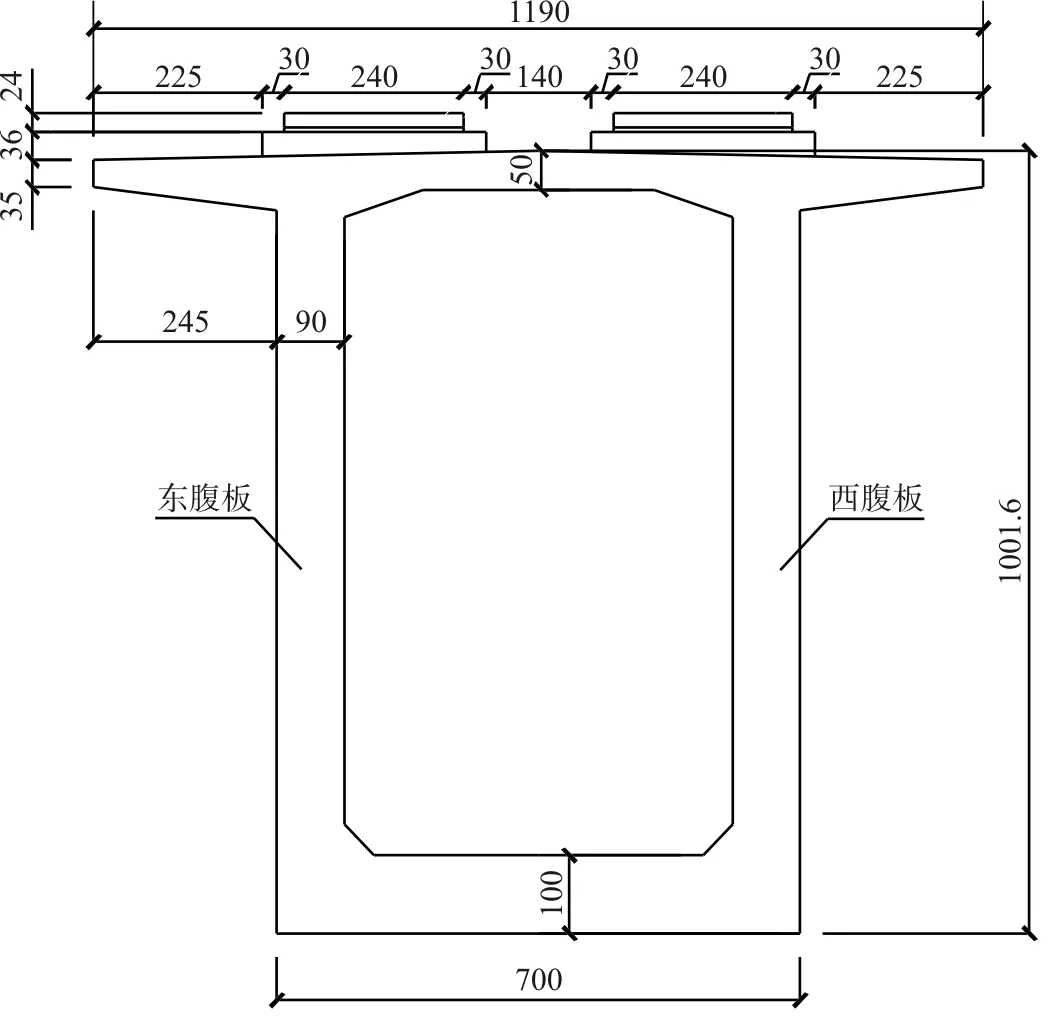
黔中水利樞紐焦家渡槽跨徑布置為9.79 m進口漸變段+15 m簡支梁+2×50 m簡支梁+(95.95+2×180+95.95)m連續剛構體系+2×50 m簡支梁+3×15 m簡支梁+14.30 m出口段，渡槽縱坡比為1/1 500。渡槽設計流量為17.783 m3/s，加大設計流量為21.002 m3/s。其中，連續剛構采用變箱截面預應力混凝土疊式箱梁結構，墩身處梁高13.8 m，合龍段梁高4.6 m，南北走向。本文有限元模擬選取的截面為3號墩9號段截面，斷面梁高10.016 m，頂板寬9.5 m，底板寬6.05 m，翼緣板長度為1.725 m，頂板厚度0.3 m，中隔板厚度0.35 m，底板厚度1 m，腹板厚度0.9 m，工程概況如圖1所示。

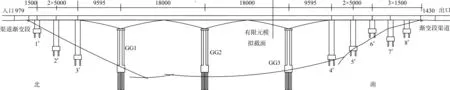
圖1 焦家渡槽工程概況(單位:cm)

2 疊箱渡槽邊界條件及熱力學參數

2.1 邊界條件

疊箱渡槽的邊界條件與鐵路、公路混凝土箱梁有所不同，其溫度邊界條件不僅包括空氣邊界，還包括水邊界。其中空氣邊界主要考慮輻射和對流，水邊界主要考慮傳導熱交換(施工階段箱內未通水，故暫不涉及)。圖2說明了疊箱渡槽與周圍環境的熱交換情況。

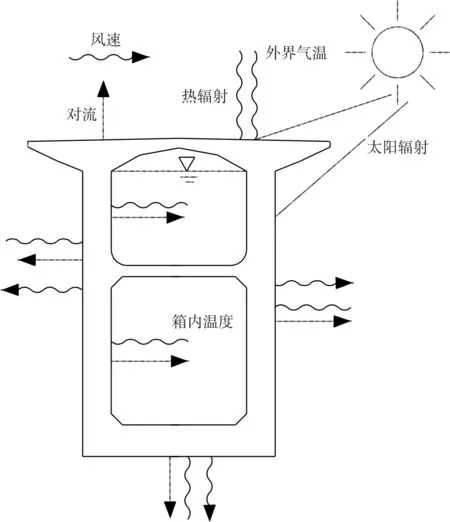
圖2 疊箱渡槽熱交換

2.1.1 對流熱交換

由對流引起的熱流密度qc采用如下計算公式：

qc=hc(Ta-Ts)

(1)

式中：hc為對流換熱系數(W/(m2·℃))；Ta為空氣溫度(℃)；Ts為結構物外表面溫度(℃)。國內外學者常用風速線性函數的經驗公式確定hc大小，本文采用李全林經過改進的經驗公式[8]：

hc=6.5+4.0ν

(2)

式中：ν為結構表面風速(m/s)。

2.1.2 長波輻射熱交換

由長波輻射引起的熱流密度qr采用如下計算公式：

qr=hr(Ta-Ts)

(3)

hr=csε[(T0+Ta)2+(T0+Ts)2](Ta+Ts+2T0)

(4)

式中：cs為Stefen-boltzman常數，取值為5.677×10-8W/(m2·K4)；ε為物體輻射率，通常小于1；T0為常數，取值為273.15。考慮到上述公式較為復雜，在實際中長波輻射熱流量并不占主要部分，結合參考文獻[8-11]，取hr=6.0 W/(m2·℃)。

2.1.3 短波輻射熱交換

短波輻射熱交換包括太陽直射、太陽散射和地面反射三部分，由短波輻射引起的熱流密度可表示為：

qs=αtI

(5)

I=Iα+Iβ+If

(6)

式中：αt為太陽輻射吸收系數；Iα為結構物外表面的太陽直射強度(W/m2)；Iβ為結構物外表面的太陽散射強度(W/m2)；If為結構物外表面所受的地面反射(W/m2)。

疊箱渡槽結構不同部位所受到的輻射情況不同，其中頂板外表面受到太陽直射、散射的作用，腹板及翼緣板外表面受到太陽直射、散射、反射等作用，底板外表面則受到地面反射作用，各部分的輻射強度I計算公式如下[8-9]：

頂板：

I=Iαsinh+Iβ

(7)

腹板及翼緣板下側：

I=Iαcosθ+Iβ/2+ρ*(Iα+Iβ)

(8)

底板：

I=ρ*(Iα+Iβ)

(9)

式中：h為太陽高度角(°)；θ為太陽入射方向與斜面法線的夾角(°)；ρ*為地面反射系數，對于一般的地面取值為0.1。

2.1.4 熱傳導方程

沿疊箱渡槽縱向溫度分布基本一致，建立二維非穩態傅立葉熱傳導方程如下：

(10)

式中：λ為混凝土導熱系數(W/(m2·℃))；c為混凝土比熱(J/(kg·℃))；γ為混凝土密度(kg/m3)。

2.2 熱力學參數

在利用有限元軟件ANSYS對疊箱渡槽截面進行二維溫度場瞬態時程分析時，其邊界條件只有空氣邊界條件。模擬計算時采用PLANE55單元，初始條件采用混凝土疊箱渡槽溫度分布較為均勻時刻，一般選取日出前后時刻。考慮到在任何時刻結構內部不可能達到絕對均勻分布狀態，在施加相應邊界條件后迭代數天來確定初始條件。材料熱力學屬性見表1。

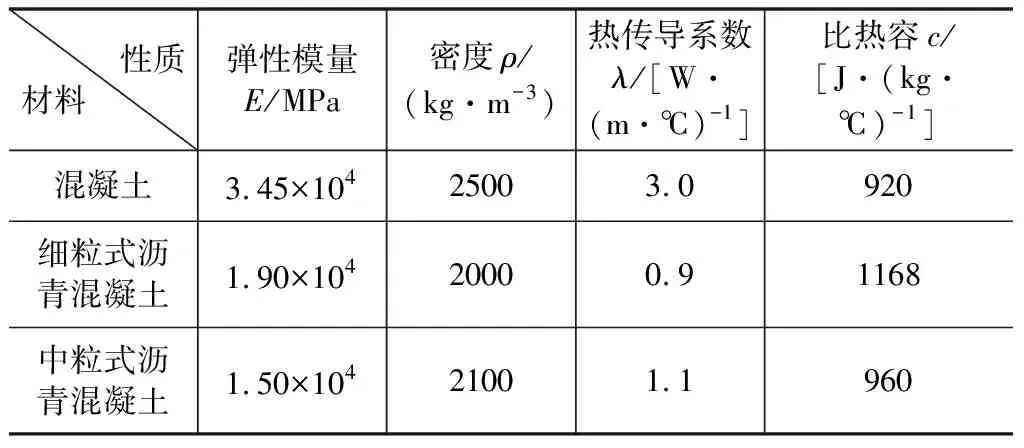
表1 材料參數

外界氣溫采用當地所測的遮陰處氣溫，上下箱室內氣溫，采用箱室內實測氣溫，混凝土表面換熱系數h為對流換熱系數hc和輻射換熱系數hr之和，所測全天風速為2～3 m/s，經計算并進行相應折減[12]，其結果見表2。

表2 混凝土表面換熱系數

3 疊箱渡槽溫度梯度曲線與鐵路橋、公路橋的對比

為研究疊箱渡槽截面溫度梯度分布形式與鐵路橋、公路橋的區別，本文選取銅玉鐵路錦江雙線特大橋(68+128+68)m連續梁和重慶石板坡公路長江大橋(86.50+4×138+330+132.5)m連續梁中與疊箱渡槽測試斷面等高(10.016 m)截面，采用有限元軟件ANSYS對其進行了溫度場計算。其中，鐵路橋采用CRTSⅠ型板式無砟軌道，混凝土底座寬3.0 m，高0.242 m，CA砂漿填充層寬2.4 m，高0.05 m，軌道板寬2.4 m，高0.19 m，總高度0.482 m，道路中心線間距為4.40 m。公路橋頂面采用瀝青混凝土鋪裝，上面層40 mm細粒式混凝土，下面層60 mm中粒式混凝土。相關的材料參數見表1，截面尺寸如圖3所示。

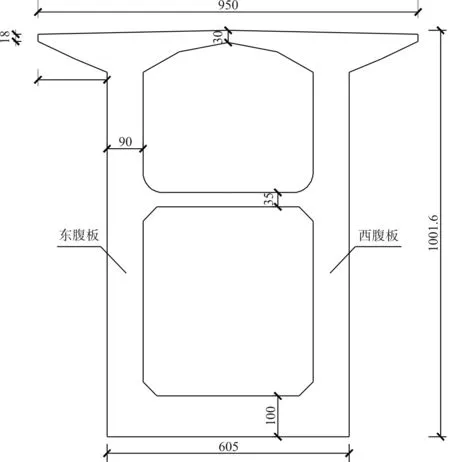
(a)渡槽截面

(b)鐵路橋截面

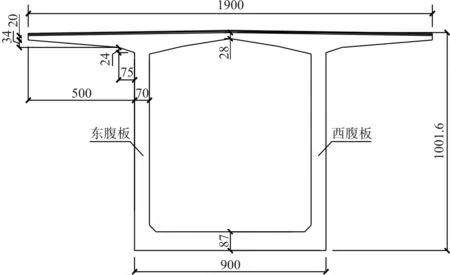
(c)公路橋截面尺寸圖3 三種橋型等高截面尺寸(單位：cm)

3.1 陰影長度的計算

橋梁走向、翼緣板長度直接影響著腹板所受太陽輻射的強弱(圖4)。

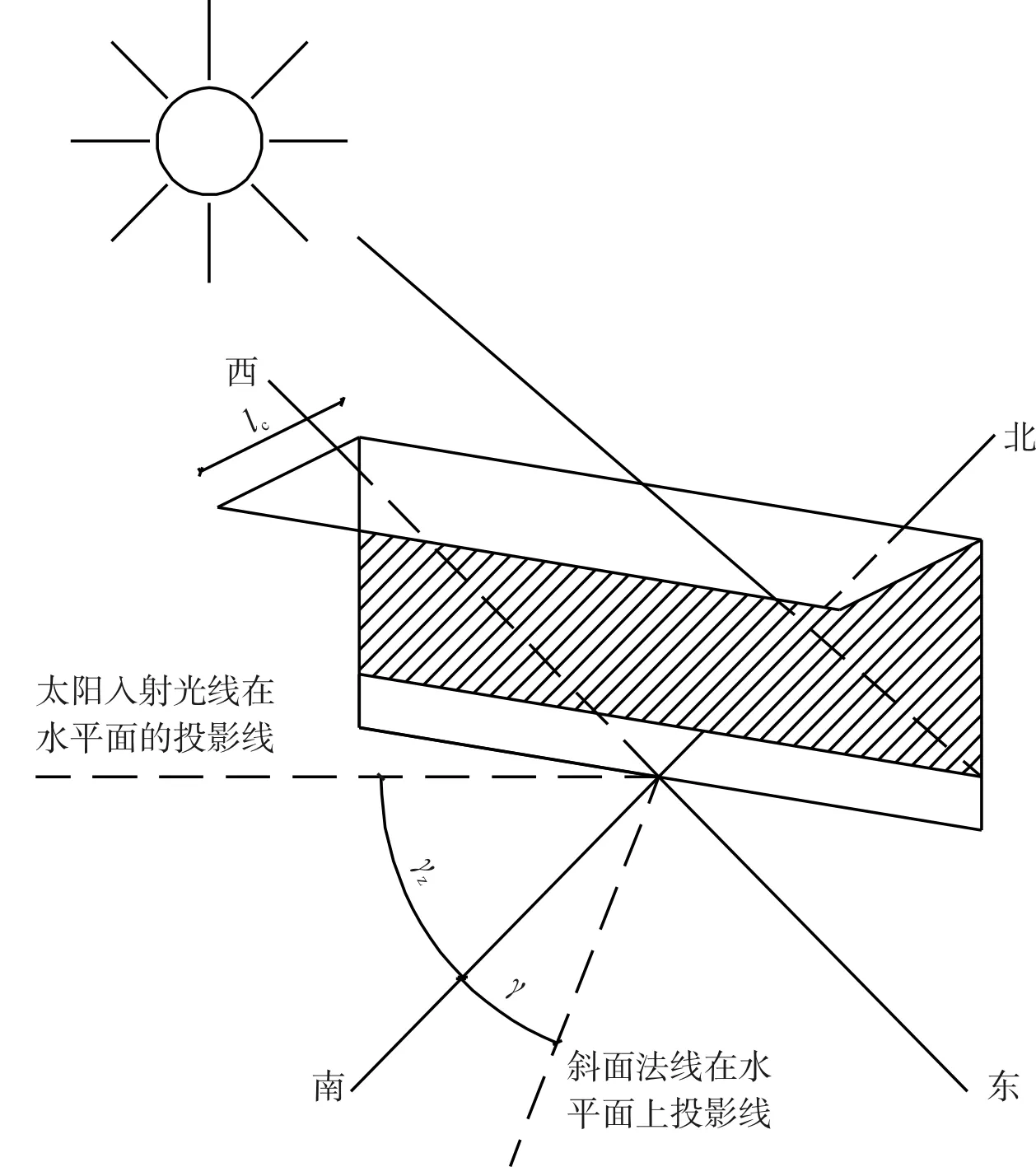
圖4 太陽輻射陰影

假設要計算的渡槽和橋梁均為南北走向，且其所處的地理位置相同，腹板不同時刻陰影長度的計算可通過圖4的幾何關系確定，即：

(11)

式中：lc為翼緣板懸臂長度；β為水平面與斜面的夾角；γ為斜面外法線的方位角；γz為太陽方位角。天文學中規定，從南出發向西為正，向東為負。

經計算，渡槽、公路橋、鐵路橋不同時刻東西腹板陰影長度見表3。由表3可以看出，由于腹板法線方向及翼緣板懸臂長度的不同，導致渡槽、鐵路橋、公路橋各時刻東西腹板的陰影長度均有所不同。

表3 東西腹板各時刻的陰影長度計算值 m

3.2 溫度梯度曲線的對比

通過計算得知，疊箱渡槽、鐵路橋、公路橋截面不同部位均存在溫度梯度，且其溫度梯度均不相同。對于豎向溫度梯度，在梗腋轉折點處溫度值較低，因此在計算中取該點溫度作為零點，其余點溫度與該點的差值作為相應點的溫差值。限于篇幅，本文只討論三種箱梁截面沿梁高豎向溫度梯度與單側腹板(東西腹板大致相同，以東腹板為例)橫向溫度梯度，各截面沿梁高方向及腹板橫向的最不利溫度梯度變化曲線如圖5所示，由此可知：

(1)從圖5(a)中看出，沿三種箱梁截面豎向高度范圍內均存在溫差，其變化規律大致接近，頂板最大溫差分別為渡槽(未通水)16.8℃，公路橋7.2℃，鐵路橋2.1℃，而腹板、底板相差卻很小。對于鐵路橋，由于其頂板上存在混凝土底座和軌道板，因此頂板最大溫差遠小于渡槽與公路橋頂板最大溫差；對于公路橋，其頂面層瀝青混凝土鋪裝層的存在導致頂板最大溫差較小，這表明鐵路橋頂板底座、軌道板和公路橋鋪裝層的存在均有利于減小頂板最大溫差。

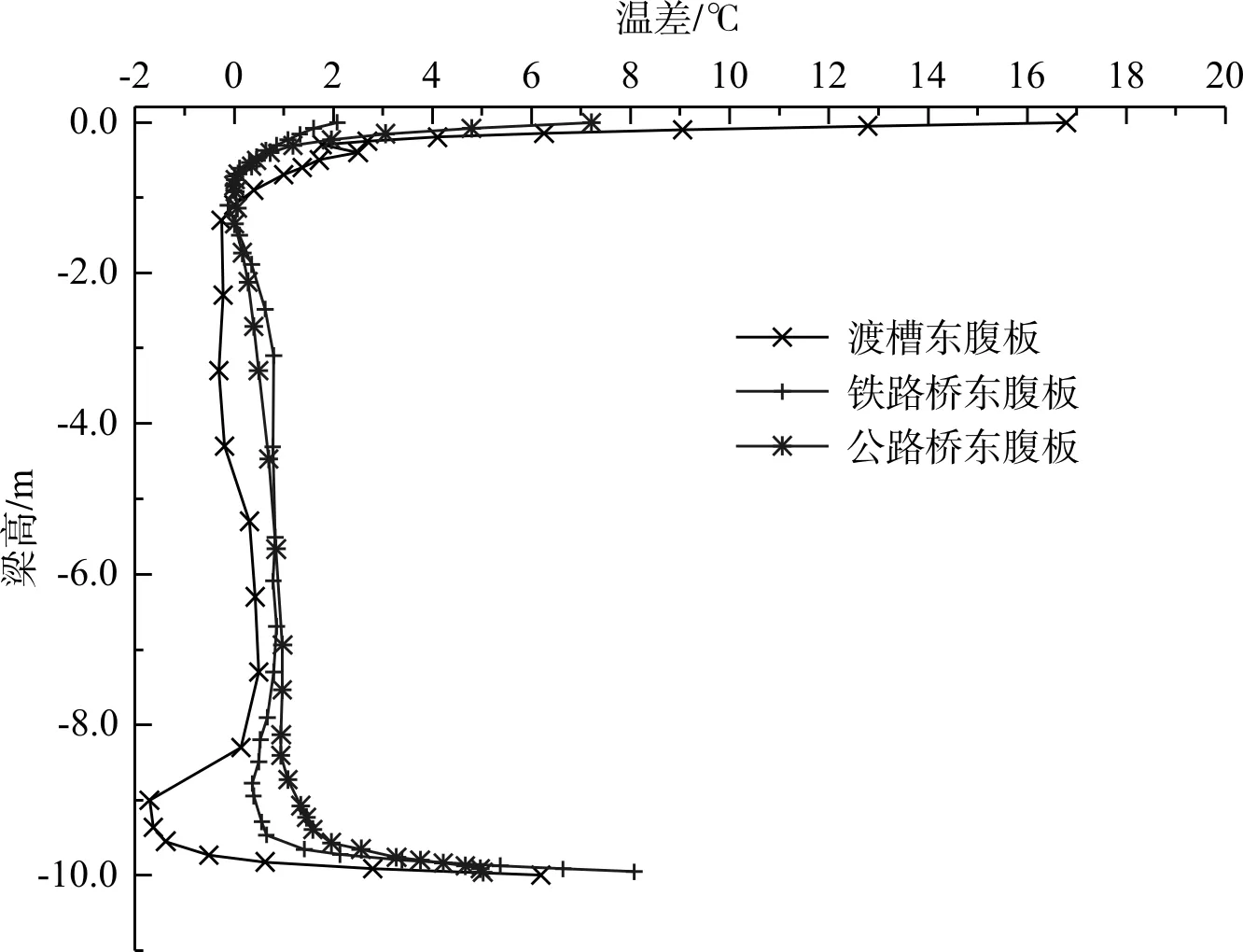
(a)三種橋型東腹板豎向溫度梯度

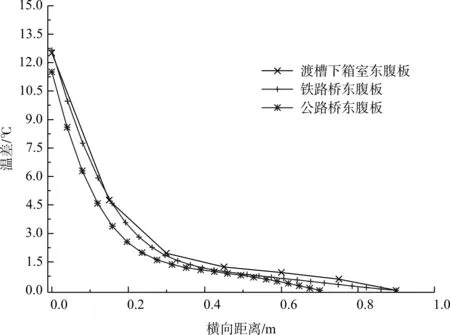
(b)三種橋型東腹板橫向溫度梯度圖5 三種箱梁模擬值溫度梯度對比

(2)從圖5(b)中看出，沿三種橋型截面腹板橫向范圍內均存在溫差，其變化規律較為接近，為非線性形式。由于翼緣板懸臂長度的不同，使得不同截面的腹板在一天中處于陰影中的時間不同，導致其最大溫差值不同。此外，不同截面相同部位混凝土板厚不同，也有可能造成不同溫差的產生。

4 結論

經計算，得到了疊箱渡槽與鐵路橋、公路橋等高截面溫度梯度曲線形式，通過對比分析，得到了以下結論：

(1)即使在不通水情況下，渡槽的頂板溫差與公路橋、鐵路橋還存在著較大差異，把鐵路橋、公路橋的規范直接拿來用是不合適的。

(2)渡槽的頂面鋪裝層有利于減小頂板豎向溫差，沿渡槽腹板橫向存在較大溫差，其溫度梯度為非線性分布。