鋼結構軸心壓桿穩定性簡析

盧啟財，趙敬義，羅光龍

((1.濟南歷下控股集團有限公司，山東濟南 250000；2.中國建筑西南設計研究院有限公司，四川成都 610042))

改革開放以來，隨著經濟突飛猛進的發展，鋼結構以其輕質高強，抗震性能好、工業化程度高、工期短等獨特的優勢得到了前所未有的發展。可以說鋼結構已經成為當前社會建設的必需品，有著不可替代的作用。

鋼結構與傳統鋼筋混凝土結構相比，由于強度比混凝土構件大很多，為了充分發揮鋼材的強度，提高截面效率，一般在設計鋼結構時，其截面輪廓較小，構件相對細長。然而，如果對于軸心受壓的鋼構件處理不當，就很有可能發生失穩的現象(圖1～圖4)，給人民的生命財產帶來巨大的損失。因此，鋼結構也有其不可忽視的缺點：結構的剛度小，穩定問題突出。

圖1 某廠房屋架桿發生彎扭失穩

圖2 加拿大魁北克大橋鋼結構失穩事故

圖3 某房屋受壓斜桿發生彎曲失穩

圖4 某廠房底層鋼結構柱失穩造成整體坍塌事故

1 結構失穩破壞的定義

結構失穩破壞是指作用在結構上的外荷載尚未達到按強度計算得到的結構強度荷載時，結構已不能承擔較大的變形，整個結構偏離原來的平衡位置而破壞或倒塌[2]。也就是說，結構的強度還沒完全發揮，就破壞啦，強度不起控制作用。鋼結構在失穩的過程中，變形會發生迅速增長，結構將在很短的時間內破壞甚至坍塌，呈現明顯的脆性破壞。鋼結構穩定性破壞的突發性，容不得人們有反應和撤離時間，造成的危害和損失是巨大和慘痛的！然而在另一方面，由于建筑效果的限制，材料和施工的缺陷等原因，鋼結構大多發生的還是穩定破壞，所以驗算鋼結構的穩定性是非常重要的！

2 軸心壓桿穩定性的理解和計算

軸心受力構件在鋼結構中應用非常廣泛，如桁架、網架中的桿件，工業廠房及高層鋼結構的支撐，操作平臺和其它結構的支柱等。除了一些較短的軸心受壓構件因局部有空洞削弱，需要驗算凈截面強度外，一般情況，軸心受力構件的承載力是由穩定條件決定的。

對于理想的軸心壓桿的整體穩定性問題，歐拉(Euler)早在18世紀就對其進行了研究。采用的是“理想壓桿模型”，即假定桿件實等截面直桿，壓力作用線與界面的形心縱軸重合，材料是完全均勻和彈性的，并得到了著名的歐拉公式。

(1)

式中：NE為歐拉臨界力；E為材料的彈性模量；A為壓桿的毛截面面積；λ為壓桿的長細比。

由歐拉公式(1)可知，我們可以通過控制壓桿的長度，加大壓桿構件截面，來增大壓桿的臨界壓力NE，保證不發生穩定破壞。

當然，實際工程中影響軸心壓桿結構的穩定性的因素很多，如構件的初彎曲、初扭曲，荷載作用的初偏心，制作引起的殘余應力，材性的不均勻等等。這些初始缺陷使得軸心壓桿一開始就會出現彎曲變形，壓桿的失穩也就成為了極值型失穩.因此實際的軸心壓桿的穩定極限承載力不再是長細比λ的唯一函數。但是，影響其穩定性的主要的、也是設計人員可控的因素還是構件的長細比λ[2]。

GB 50017-2003《鋼結構設計規范》(下面簡稱《鋼規》)中，對于軸心壓桿的穩定計算公式如下：

(2)[1]

式中：N為軸心壓力；A為構件的毛截面面積；φ為軸心壓桿的穩定系數(取截面兩主軸穩定系數的較小者)；f為鋼材的強度設計值。

從公式2可以看出，對于單根受壓桿件，其相比于強度計算公式，穩定計算公式多了軸心壓桿穩定系數φ。軸心壓桿的穩定系數φ是穩定性理論和統計分析結果在公式中的集中體現，達到了極簡和實用的目的。穩定系數φ的計算也是軸心壓桿穩定驗算的難點和關鍵。其計算方法和步驟，筆者總結歸納如下：

(1)對雙軸對稱截面：

第一步：確定構件截面類型(a,b,c,d)，通過查《鋼規》表5.1.2.1-1和表5.1.2.1-2；需要注意的是《鋼規》表5.1.2.1-1是對于厚度小于40 mm的構件而言，而《鋼規》表5.1.2.1-2是對于厚度大于或等于40 mm的構件而言。

第二步：計算截面的回轉半徑ix和iy；

第三步：確定構件的計算長度lx和ly；

第五步：計算軸壓穩定系數φ。有兩種方法可選用。

其中：fy為材料的屈服強度。

當λn≤0.215時：φ=1-α1λn2；

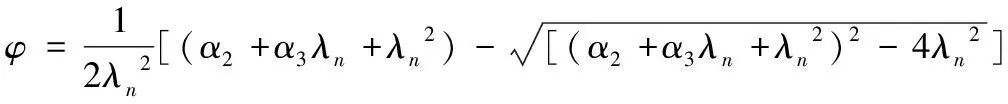
式中：α1、α2、α3按《鋼規》表C-5查詢得到。

(2)對于單軸對稱的截面(比如T形鋼)，因為還可能發生繞對稱軸方向的扭轉失穩。故在計算繞對稱軸的長細比時，須先經過公式(3)的處理，再用λyz代替λy[1]

(3)[1]

(4)[1]

i02=e02+ix2+iy2

(5)[1]

式中：e0為截面形心至剪心的距離；i0為截面對剪心的極回轉半徑；λy為構件對對稱軸的長細比；λz為扭轉屈曲換算長細比；It為毛截面扭轉慣性矩；Iw為毛截面扇性慣性矩；對T形截面(軋制、雙板焊接、雙角鋼組合)、十字形截面和角形截面可近似取Iw=0；A為毛截面面積；lw為扭轉屈曲的計算長度。

(3)由于截面的不同，軸心壓桿的失穩狀態主要呈現三種，分別為彎曲失穩，如雙軸對稱的工字鋼截面(圖5)；彎扭失穩，如單軸對稱的T形截面(圖6)；和扭轉失穩，如雙軸對稱的十字形截面(圖7)。

三種失穩的狀態對應的臨界壓力的計算方法也不盡相同，對應的臨界壓力值也是相差很大。因此，在設計軸心壓桿的時候，應特別注意截面的選擇。

比如某軸心受壓實腹桿件，軸心壓力設計值(包括構件自重)N=1 500 kN，計算長度lx=ly=3m；擬采用Q345B鋼材，我們分別選用同樣截面面積的焊接組合工字形鋼(翼緣鋼板為火焰切割邊)(圖8)與焊接T型鋼(圖9)，并對比兩者在荷載作用下穩定應力的大小。

當采用圖8所示焊接組合工字形鋼(翼緣鋼板為火焰切割邊)時，查《鋼規》表5.1.2.1-1可知截面為b類截面，且截面參數如下:

截面面積A=25×1.2×2+25×0.8=80 cm2

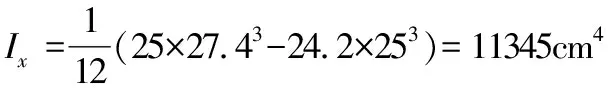
圖5 彎曲失穩示意

圖6 彎扭失穩示意

圖7 扭轉失穩示意

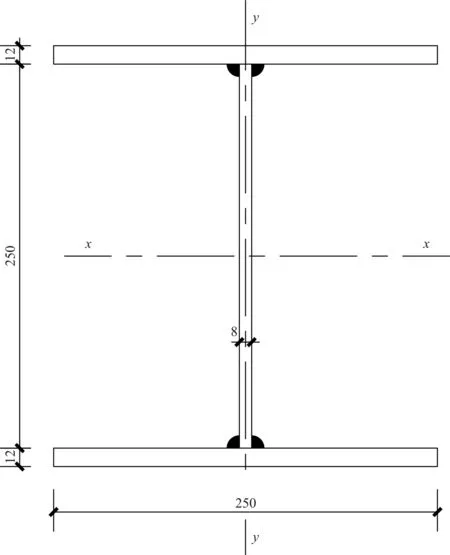
圖8 焊接組合工字形鋼截面

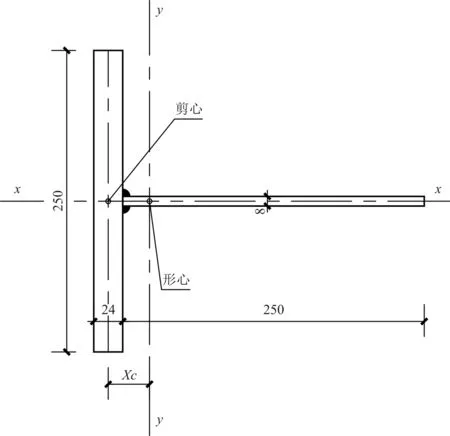
圖9 焊接T型鋼截面

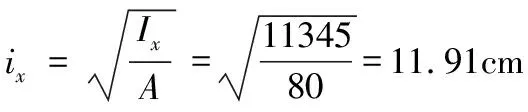
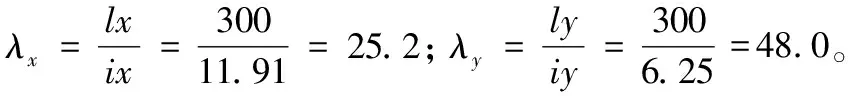
b類截面，按《鋼規》表C-5，查得α1=0.65、α2=0.965、α3=0.30,

計算軸心壓桿穩定系數φ：

=0.8169

根據公式2，計算得到壓桿穩定應力：

(b)當采用圖9所示焊接T形截面時，查《鋼規》表5.1.2.1-1可知截面對x軸為C類截面，對y軸為b類截面且截面參數如下:

截面面積：A=25×2.4+25×0.8=80cm2

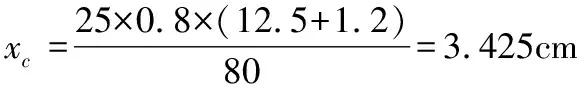
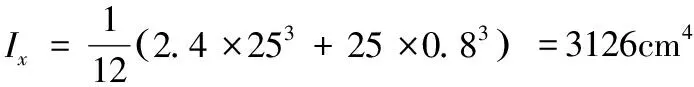
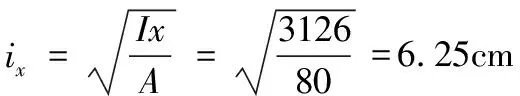
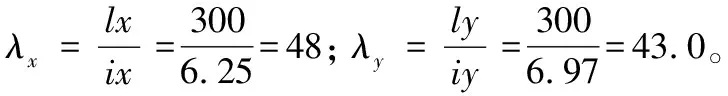
T形截面的剪力中心在翼緣板和腹板中心線的交點，所以截面形心至剪心的距離e0的距離等于xc，即：

e0=xc=3.425cm

截面對剪心的極回轉半徑：

i02=e02+ix2+iy=3.4252+6.252+6.972=99.38 cm2

對于T形截面，毛截面慣性矩：Iw=0；

扭轉屈曲換算長細比：

則換算長細比：

=52.45

用λxz=52.45代替λx

由于繞x軸和繞y軸失穩的截面類型分別為c類和b類。故下面分別驗算,以求得較大軸壓穩定系數φ。

對x軸(c類)：

求得正則化長細比：

計算穩定系數φ：

c類截面，且λn=0.6832≤1.05,按《鋼規》表C-5，查得α1=0.73、α2=0.906、α3=0.595

=0.6852

對y軸(b類)：

求得正則化長細比：

計算穩定系數φ：

b類截面，按《鋼規》表C-5，查得α1=0.65、α2=0.965、α3=0.30

=0.8466

φ取φx和φy的較小值，即：φ=φx=0.6852

根據公式(2)，計算得到壓桿穩定應力：

通過上述實例驗算可知：相同荷載作用下的軸心壓桿，截面面積相同的工字鋼和T形鋼的穩定應力分別為229.5 Mpa左右和273.6 Mpa，兩者相差44.1 Mpa!故雙軸對稱的工字鋼比單軸對稱的T形鋼的整體穩定性能更好！

3 結束語

鋼結構應用普遍，穩定性問題突出。既和鋼材的缺陷、施工的質量相關，更與設計人員的穩定性概念和意識相關。對軸心受壓，一方面，應適宜的控制構件的長細比；另一方面，應盡量采用雙軸對稱的截面，以達到安全可靠，經濟合理的目標。