航空發動機葉片焊接軌跡規劃研究
宋 濤 ,趙 萌 ,戴士杰 ,,王志平
(1.河北工業大學 機器人及其自動化研究所,天津 300132;2.天津航空機電有限公司,天津 300308;3.中國民航大學 天津市民用航空器適航與維修重點實驗室,天津 300300)
1 引言
近年來,我國民用航空工業迅猛發展,取得很多重大科研成果,但是在很多領域尚有很多的技術難題沒有攻克。在這些領域中,如何解決發動機葉片的保養、維修等問題占據了較大的比重,尤其是民用發動機葉片的維修。國外研發了很多自動焊接系統,其共同特點是將精確、快速的光學測量技術、高精度的機械裝置進行合理的集成,成功解決了葉片焊接修復質量穩定性不高的難題,但是技術對中國壟斷。文獻[1]對6自由度工業機器人的點到點和多目標空間軌跡規劃提出了最優軌跡規劃方法,在保證焊接質量的前提下進一步提高了焊接機器人的焊接效率。文獻[2]提出了弧焊機器人系統的基于視覺的整體路徑生成辦法。文獻[3]研究了一種接管焊接軌跡修正辦法,解決了兩接管存在尺寸誤差、加工誤差及熱變形等問題。文獻[4-5]提出了弗萊納-雪列矢量法解決焊接軌跡中離散點坐標系建立問題,但是由于太靠近焊接工件,不方便擺放焊槍位置。文獻[6]運用遺傳算法和主從機器人協調操作得到兩臺機器人最優焊接軌跡,但是該方法只適用于長尺寸整體薄壁板。在葉片焊接以及維修方面,國內起步較晚。且對航空發動機葉片焊接修復技術的研究與應用目標全部是軍用航空發動機;焊接修復工藝主要集中在激光熔敷和TIG焊上,在發動機葉片自動化焊接修復方面的研究與國外差距甚大,極其缺乏核心共性技術。
2 葉片截面與B樣條建模
k次B樣條曲線可以表示為:
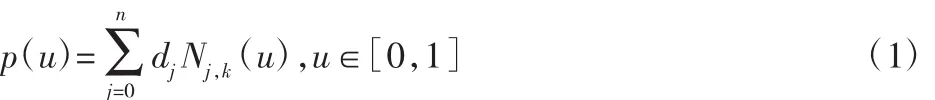
式中:d—控制點,順序練成的折線稱為B樣條控制多邊形;Ni,k(u)(i=0,1,…,n)稱為 k 次規范 B 樣條基函數;u—節點矢量參數,并且按照非遞減順序排列。
對已有的三維測量得到的點云數據擬合處理,并對得到的缺失部分分層。考慮到壓氣機葉片高度扭曲的特點,其對應的葉片截面也是由若干個分段函數組成。傳統的樣條曲線以及Bezier曲線不具有B樣條曲線特有的局部支撐性[7],對葉片擬合會出現較大誤差。焊絲在正常進給速度與送絲速度下其焊接余高在1mm到1.3mm之間。由于葉片焊接維修部分所堆焊部分層數不會超過5層,且葉片在高度向的法截線曲率并不大,為了實現對葉片截面多層堆焊,我們對已有模型進行等厚分層處理[8]。
3 B樣條軌跡規劃
由于在焊接熱輸入焊縫的過程中,熱輸入過大、缺乏融合和焊接變形是影響零件成型質量的重要因素。對焊接路徑的不同部位的堆積將在成形過程中影響零件的熱傳遞,從而影響成形精度。因此,必須采用恰當的堆積軌跡。修復葉片葉尖時最大的焊接寬度為2.12mm,修復葉片頂端時最大修復寬度為2.66mm,所使用的焊絲直徑為1mm,且切片的輪廓呈圓弧狀,對此我們提出了B樣條沿中線焊接的方式。該方法保留了輪廓掃描法焊接精度高的優點,還能避免輪廓掃描法中焊道間距過窄導致余高過高的現象。使用沿中線焊接的方式,只需在焊接時改變焊接參數,即可達到高精度高質量焊接的目的,使得焊接工藝變得簡單易操作。
3.1 等弧分割曲線
葉片邊緣曲線的中線可以表達葉片邊緣曲線的變化趨勢,這是采取中線作為焊接路徑的重要原因。因此,提取的中線必須沿著邊緣曲線變化方向伸展,這就和邊緣曲線的曲率變化密不可分,航空發動機的葉片截面曲線曲率變化平緩,在一定的采樣密度下可以采用等弧長分割的方式分割曲線,提取出來的中線滿足焊接路徑的精度要求。
該段曲線的長度,用曲線積分可以很容易的表示出來,這時上端曲線和下端曲線共有n+1個點,并在計算機里將上端曲線和下端曲線平分成n等份。這時我們等弧長比例分割曲線,如圖1所示。可以證明A1B1的中點即為B樣條的第二個型值點P1,按此方法可以依次求得P2、P3、P4……
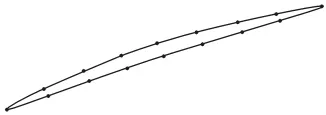
圖1 等弧長分割曲線Fig.1 Curve of Equal Arc Length
該方法保留了輪廓掃描法焊接精度高的優點,還能避免輪廓掃描法中焊道間距過窄導致余高過高的現象。使用沿中線焊接的方式,只需在焊接時改變焊接參數,即可達到高精度高質量焊接的目的,使得焊接工藝變得簡單易操作。找到上下兩段曲線中對應的端點A、B,可求出兩個端點之間的中點坐標P,如圖2所示。通過對中點坐標進行B樣條逼近運算就可以得出葉片的邊緣曲線的中線方程,也就是航空發動機葉片的焊接修復路徑。
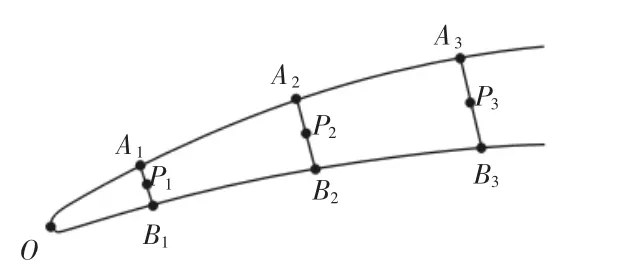
圖2 等弧長分割曲線的中點求取(局部放大)Fig.2 Midpoint of Arc Length Segmentation Curve(Local Amplification)
3.2 B樣條逼近及其沿曲率調整
在這里考慮三維測量后點云擬合時由于前、后表面特殊形狀造成的影響,由于我們之前對三維模型進行了三維測量,得到點云數據后擬合。對于分段曲率不同的前后表面,由于OA面曲率大,點云分散,曲面擬合的時候誤差較大。我們假設OA邊曲率為C2,OB邊曲率為C1。有:

δ與擬合誤差大小相關。
又因為A1P1+B1P1=A1B1,得到A1P1和B1P1如下:
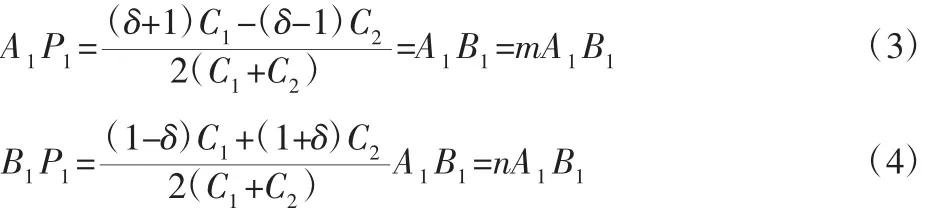
式中:m+n=1,并且當且僅當δ=1時,P點為AB的中點。
采用累計弦長參數化[9-10]方法參數化B樣條曲面的型值點。
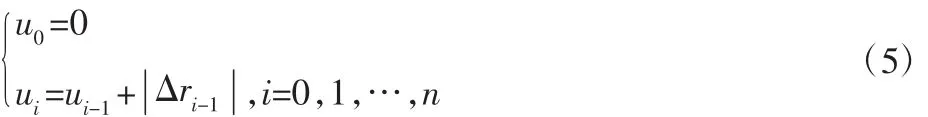
式中:Δr—向前差分矢量,矢量r的前后兩個相鄰矢量差是弦線
矢量,這樣就如是反映了數據點按弦長的分布情況。型值點確定的情況下,基函數Nj,k(u)由節點矢量U決定,我們采用平均統一的方法對節點配置[10]。并建立求解未知控制頂點的線性最小二乘問題,即試圖尋找一條k次B樣條,使得B 樣條曲線 p(u)在滿足兩個端點
(等弧長分割的端點)不變的情況下,其余各個點在最小二乘意義下逼近。為了除去兩個端點,我們引進m(u)函數。,其目標函數:
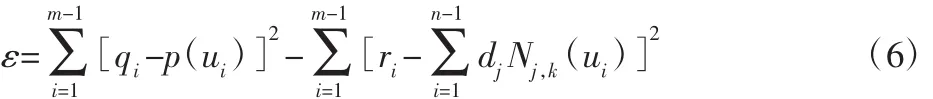
若殘差為實際數據點與擬合點之間的差值,按照線性最小二乘理論需要殘差的平方和最小,對d求偏導數得到:
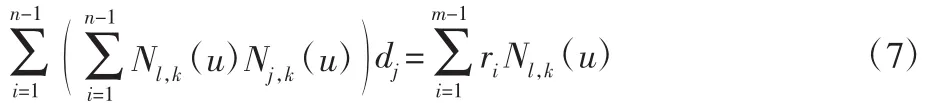
此時的R是在有誤差意義下的A、B的中點,得到含有n-1個未知參量的線性方程組:

就得到了控制頂點D的位置,如圖3所示。用公式表達即:

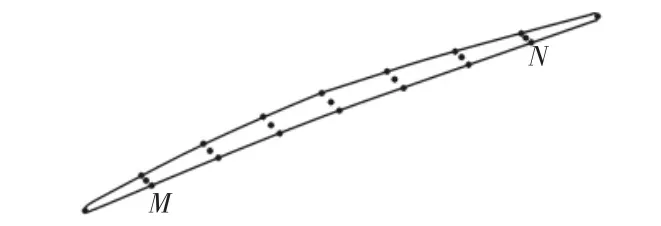
圖3 B樣條型值點求取Fig.3 B-Spline Type Value Points
4 實例仿真
通過對航空發動機壓氣機第六級葉片葉尖磨損情況下得到的待修復模型經過分層處理,求取輪廓曲線方程后分割曲線,獲取中點后,將離散的中點坐標輸入計算機中,得到MN兩點之間的曲線,如圖4所示。這樣,經過B樣條逼近,成功得到了焊接葉片邊緣曲線的中線,也就得到了航空發動機葉片的焊接軌跡。
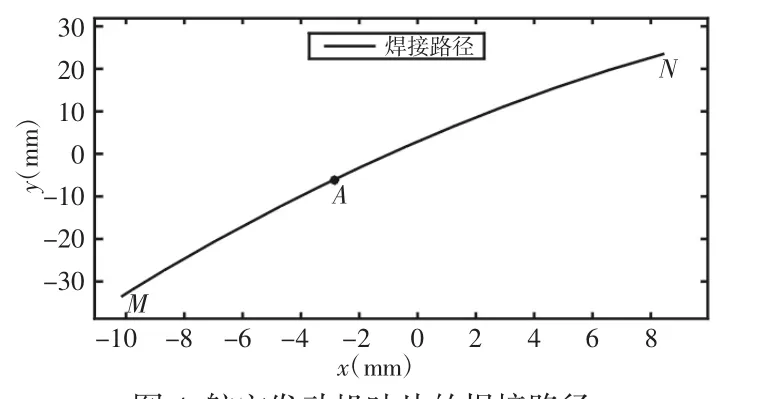
圖4 航空發動機葉片的焊接路徑Fig.4 Welding Path of Aero Engine Blade
通過仿真可以得出航空發動機葉片焊接修復軌跡,焊接路徑曲線的精度對于實際葉片維修精度具有直接的影響,如果通過B樣條逼近得到的路徑曲線較大偏離了真實的焊接路徑,就會大大降低葉片的焊接修復質量,甚至可能導致后續磨削已焊接葉片的時間大大超過焊接葉片本身所需的時間。這里對比已經用于生產的一種焊接機器人的實際焊接軌跡,實際焊接軌跡是由若干個曲線逼近軌跡點,并做了示教調整之后得到的,其軌跡點路徑可以從機器人程序中得到。下圖展示了焊接機器人現場焊接與自行設計的柔性焊接夾具,如圖5所示。

圖5 焊接機器人與夾具Fig.5 Welding Robot and Fixture
試驗中先是采用了9個點經過B樣條擬合得到的焊接路徑曲線,倘若將上下兩端弧長按等弧長劃分法得到100個端點,也就是將兩段弧各分為99段,再通過次B樣條擬合處理,得到的曲線更加貼合實際,甚至可以忽略曲線的誤差,用得到的曲線代替理論上的焊接路徑曲線。其中,航空發動機葉片的理論焊接路徑是分為99段圓弧后逼近計算的曲線,實際焊接路徑是由若干段曲線逼近軌跡點計算出來的曲線。由于對邊緣曲線進行過多段的等弧長劃分會導致生成的焊接路徑曲線由大量曲線段構成,這無疑增加了計算時間,降低了焊接修復效率,同時在每段小曲線端點處的曲率往往變化很大,從而使焊槍運動時產生較大震動,影響葉片焊接修復精度,甚至影響焊接機床的使用壽命,所以不能對分層后的邊緣曲線進行弧長過短的等弧長劃分。根據實際情況,合理制定焊接路徑曲線的精度要求才能保證高效的生成滿足葉片焊接修復質量的焊接路徑,這里取(0.02~0.05)mm是完全能符合焊接工藝要求的。A點附近焊接理論路徑與實際路徑的局部放大圖,如圖6所示。對比構造的兩條焊接路徑,如圖6所示。將實際曲線上每點到理論曲線的最短距離作為評判曲線誤差的標準,在計算機中得到理論焊接路徑與實際焊接路徑誤差曲線,如圖7所示。

圖6 葉片的理論焊接路徑與實際焊接路徑(局部圖)Fig.6 Theoretical Welding Path of Blade and Actual Welding Path(Local Graph)

圖7 理論焊接路徑與實際焊接路徑的誤差曲線Fig.7 Error Curve of Theoretical Welding Path and Actual Welding Path
5 結論
主要提出了一種航空發動機葉片焊接修復路徑的方法。對三維測量得到的點云數據擬合處理,考慮擬合時候測量的誤差以確定沿曲率的修正辦法,并對得到的缺失部分分層,在層與層之間通過分析得出延中線焊接的方法,其重點工作是對截面曲線等弧長分割和B樣條擬合得出焊接軌跡。并在計算機中分析實際焊接軌跡和理論焊接軌跡,誤差曲線顯示出構建的實際焊接路徑曲線最大誤差不超過0.02mm,根據葉片焊接修復質量要求,實際的焊接精度要小于0.2mm,所以可以得出結論,所構建的焊接路徑滿足工藝要求,能夠使焊接厚的葉片到達所需精度。同樣,航空發動機壓氣機葉片的葉頂部分焊接修復的焊接路徑生成與焊接路徑精度的檢測也可按上述過程實現。

