用不變本征算符法求晶面吸附原子的振動模?

張科1)2)3) 范承玉1)? 范洪義2)

1)(中國科學院安徽光學精密機械研究所,中國科學院大氣光學重點實驗室,合肥 230031)2)(中國科學技術大學研究生院科學島分院,合肥 230031)3)(淮南師范學院電子工程學院,淮南 232038)(2018年3月17日收到;2018年5月20日收到修改稿)

1 引 言

固體物理學主要研究固體的物理性質、微觀結構、固體中各種粒子運動形態和規律以及晶體的振動模[1].從理論體系來看,包括微觀理論與宏觀理論:一方面在原子、分子水平上運用經典理論和量子理論研究固體表面的組成,原子結構及輸運現象、電子結構與運動及其對表面宏觀性質的影響等;另一方面在宏觀尺度上,從能量的角度研究一系列的表面與界面現象,在實驗的基礎上建立對應的基本方程[2,3].近年來,由于各種功能器件的發展,促進了關于半導體陶瓷等各種功能材料表面與界面的研究;又由于各種新型復合材料的發展,對表面與界面的研究提出了新的課題.因此,關于各種材料表面與界面物理、化學性質的研究,已成為當前高科技尖端科學領域中的重要組成部分,是一個急待開發的方向[4,5].

表面物理與界面物理學的一個基本問題是晶體表面吸附一個原子以后晶格振動的變化情況[6].晶格振動是指晶體中的原子在做集體振動,其振動的頻率對應于系統的能級差(能帶).由于晶體原子間的相互作用,原子的振動不是孤立的,且晶格具有周期性,并以波的形式在晶體中傳播,形成所謂的格波.一個格波表示晶體所有原子都參與的頻率相同的(簡諧)振動,常稱為一種振動模.晶體振動模的研究一直受到國內外學者的廣泛關注.中國科學技術大學基礎物理中心的蔣最敏等[7]利用解動力學矩陣的方法計算了硅(111)面不同層數體系的所有表面振動模.福州大學物理系的洪水力[8]根據分子晶體的特征,應用空間群商群與點群同形原理,并配合結構分析方法,直接對RbC8H5O4晶體中的內振動模按不可約表示相容關系進行對稱性分類.華中理工大學物理系安忠等[9]從計及了鏈間相互作用項的Su-Schrieffer-Heeger(SSH)模型出發,討論了相鄰兩條鏈間電子躍遷對反式聚乙炔中孤子能譜及孤子附近的局域振動模的影響.浙江大學的李宏年等[10]對單層納米碳管振動模的拉曼光譜進行了詳細研究,測量了單層納米碳管的一級、二級拉曼光譜,通過與理論值對照,對這些譜線做了初步標定.河北師范大學物理學院的謝尊等[11]基于擴展的二維SSH模型,研究了庫侖釘扎作用對聚噻吩中雙空穴極化子附近的局域振動模的影響.Jumeau等[12]對低密度聚乙烯中特定的自由基CH2的拉曼振動模式進行了詳細研究,確定了不同的非晶和結晶拉曼匹配.晶格振動模的一般求解方法是以牛頓運動學方程為基礎寫出晶格的振動方程,而后根據周期性條件設其有行波解代入求解[13?15].但是,該方法在有表面雜質的情況下不適用,以至于在表面吸附位勢系數β0與晶體內部周期位勢系數β不同的情況下,晶體表面吸附一個質量為m0(與晶格原子質量m不同)的原子以后晶格的振動模一直未見文獻報道.本文采用文獻[16,17]中提出的不變本征算符方法,嚴格地推導出了這種吸附情形下晶體振動模的詳細表達式,并討論了振動模與吸附原子質量和晶體內位勢的變化關系.本文所用方法簡潔明了,無需涉及系統的具體量子態和波函數.

2 不變本征算符方法

不變本征算符[18,19](invariant eigen-operator,IEO)方法來源于量子力學的Schr?dinger方程與Heisenberg方程的和諧[20,21].Schrdinger把和哈密頓算符H看成等價,因此在很多參考文獻里被稱為Schr?dinger算子.Schr?dinger方程為

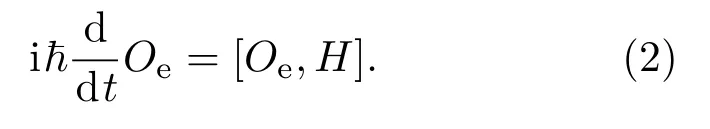
則有

方程(4)可以看作是和能量本征態方程(1)“平行”的方程,換句話說,算符Oe在的作用下是“不變量”.這樣,如果算符Oe滿足(3)式,就稱它為系統的一個“一階”不變本征算符.在波函數的定態本征方程中,本征值E即代表系統的能量.而在引入的算符本征方程中,本征值λ與系統哈密頓量的本征能譜有密切關系,它對應的是系統的能級差.

再根據(3)式有

由于Oe是非零算符, 必然存在|?〉a和|?〉b使得a〈?|Oe|?〉b/=0,于是

即λ是系統的一個能級差.例如,一維諧振子的哈密頓量H1為

所以a就是一維諧振子的哈密頓量H1的“本征算符”,相應的本征值為ω,也是系統的能級差,這符合已知量子力學中的結果.

此時Oe稱為“二階”不變本征算符.由于對應于H2,所以就是兩個相鄰能級間的能隙.用類似于(6)式的證法可以說明這一點,即

對一個系統的哈密頓量H,事先選定算符Oe作為這個系統的不變本征算符,按照(3)式從一階開始做試探計算,若做一次對易子就有[Oe,H]= λOe,那么該體系的能隙就是λ,若做一次和二次都不滿足算符方程,當做n次對易計算后有

借助IEO方法,充分利用海森伯方程,則無須涉及系統的具體量子態和波函數,就可以簡捷方便地得到某些量子系統的能量本征值.對于固體物理中有復雜周期結構的哈密頓量,用IEO方法求系統的準粒子譜頗為有效.

3 吸附原子的晶面作為半無限原子鏈系統的振動模

圖1所示是一個半無限原子鏈系統,一邊無限延伸,另一邊吸附一個原子,質量為m0,它不同于原子鏈中的原子質量m,只考慮相鄰原子之間的相互作用,吸附原子的作用系數為β0,內部作用系數為β.

如圖1所示,吸附原子后晶格的哈密頓量為[22,23]

圖1 吸附原子、吸附常數不同于晶體內部的半無限原子鏈模型Fig.1.The adatom and adsorption constant are different from those within the crystal of the semi-In finite atomic chain model.

其中P0是吸附原子的動量,Pn為其他原子的動量.

利用量子力學基本對易關系導出:

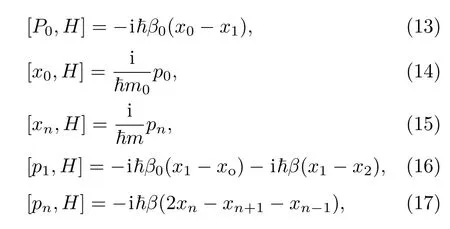
以及

設不變本證算符的形式為

其中η,α為待定,代入本征算符方程得到

利用上述對易關系,(22)式化為

其中,

將(24)和(25)式代入(23)式得到:

比較本征算符的形式(21)式得到

所以根據(10)式下的討論可知,振動模式為

由(27)式可以連續求出:

聯立解方程(29)和(30)可得:

4 討 論

1)當?=1,m/=m0,β = β0時,代入(32)式,得到

則系統的振動模式為

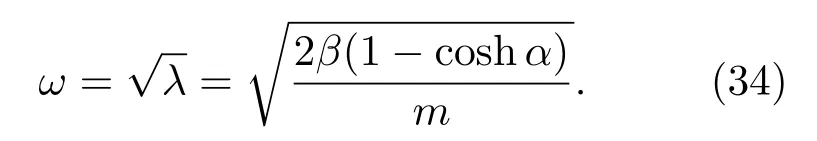
又由α0＞ 0得出

由于m和m0都是正數,上述不等式可以導出m＞2m0,這就是形成穩定振動模的吸附條件.

2)當?=1,m=m0,β /= β0時,代入(32)式,得到

則系統的振動模式為

該結論與文獻[13–15]的結果完全一致.

為了得出有意義的結果,有|eα|＞1.再代入(36)式,得到

這是形成穩定振動模必須的吸附條件.

為了詳細研究振動模ω與晶體內部原子的勢常數β,晶格原子質量m、吸附原子質量m0的變化關系,我們分別繪出了相應的圖形.

在圖2中,設定β0=0.5,m0=1,做出了m=0.1,0.2,0.3,0.7四種情況下的晶格振動模ω與作用系數β的變化關系.從圖中可以看出:1)在m0固定的情況下,ω隨著β的增加而增加,在β趨向β0時ω趨向無窮大;2)對于相同的β值,m值越大,ω值越小.

在圖3中,設定β0=0.5,β=0.1,做出了m0=0.1,0.2,0.3,0.7四種情況下的晶格振動模ω與晶格原子質量m的變化關系.從圖中可以看出:1)當作用系數β,β0固定,ω隨著m的增加而減小,最終趨于恒定值;2)衰減速度以及恒定值的大小隨m0的增加而降低.

圖2 晶格振動模ω隨作用系數β的變化Fig.2.The relation between lattice vibration mode ω and the coefficient β.

圖3 晶格的振動模ω隨晶格原子質量m的關系Fig.3.The relation between lattice vibration mode ω and lattice atom mass m.

圖4 晶格的振動模ω與吸附原子質量m0的關系Fig.4.The relation between lattice vibration mode ω and absorbing atom mass m0.

在圖4中,設定β0=0.8,m=0.3,做出了m0=0.3,0.5,0.7,1.0四種情況下的晶格振動模ω與吸附原子質量m0的變化關系.從圖中可以發現:1)當m,β0固定時,ω隨著β的增加而增加,當β=β0時,趨向于無窮大;2)對于不同的m0值,在β0取較小值時,m0越小ω越大;隨著β0的增大,m0越小ω越大.

5 結 論

采用不變本征算符方法嚴格推導出了晶體表面吸附一個質量為m0(與晶格原子質量m不同)的原子以后晶格的振動模,而且表面吸附勢常數β0與晶體內部勢常數β不同,嚴格地推導出了振動模的表達式,并分析了振動模ω與晶體內部原子的位勢β,晶格原子質量m、吸附原子質量m0的變化關系.發現:1)在m0固定的情況下,ω隨著β的增加而增加,在β趨向β0時ω趨向無窮大;2)對于相同的β值,m值越大,ω值越小;3)當作用系數β,β0固定,ω隨著m的增加而減小,最終趨于恒定值;4)衰減速度以及恒定值的大小隨m0的增加而降低;5)當m,β0固定時,ω隨著β的增加而增加,當β=β0時,趨向于無窮大;6)對于不同的m0值,在β0取較小值時,m0越小ω越大;隨著β0的增大,m0越小ω越大.