Hom-Leibniz超代數的廣義導子

姚光同，賈 璐

(山東工商學院數學與信息科學學院，山東 煙臺 264005)

1 預備知識

Hom-型代數是在原有代數基礎上，將其定義代數的等式用一個或幾個線性映射(稱為扭曲映射)進行扭曲，從而得到的一類新的代數.當扭曲映射是恒等映射時，Hom-型代數便退化為原來的代數.為了刻畫Witt代數和Virasoro代數的某些形變結構，Hartwig等[1]給出Hom-李代數的概念，從而開始了對Hom-型代數的理論研究.Hom-型代數與數論、Yang-Baxter方程、量子群等都有聯(lián)系.[2-5]

1993年，Loday等[6]給出一種非對稱代數的同調，從而Leibniz代數的概念被確定.與李代數相比，Leibniz代數的定義中少了反對稱的條件，因此Leibniz代數是李代數的推廣，Leibniz超代數是李超代數的推廣.[7]Hom-Leibniz代數可以看成是Hom-李代數的推廣[8]，因此，Hom-Leibniz超代數可以看成是Hom-李超代數的推廣[9]，即Hom-Leibniz超代數包含Hom-李超代數、Hom-李代數、Hom-Leibniz代數、李代數、Leibniz超代數等.

導子和廣義導子代數在李(超)代數的研究中有重要的地位.[10-11]本文將文獻[4-5]中的結果推廣至Hom-Leibniz超代數，主要研究Hom-Leibniz超代數L的廣義導子(導子代數Der(L)、擬導子代數QDer(L)、中心導子代數ZDer(L)、型心代數C(L)、擬型心代數QC(L))的重要性質及其之間的關系.

定義1.1[5]設(L，[，]，α)是一個三元組.其中：L為域K上的Z2-階化線性空間；[，]：L×L→L滿足偶雙線性，即[Lθ，Lμ]?Lθ+μ；α：L→L是偶線性映射.記hg(L)是L的所有齊次元的集合，(-1)x的x表示x的階化次數.若?x，y，z∈hg(L)，有：(1) [x，y]=-(-1)xy[y，x]；(2) (-1)zx[α(x)，[y，z]]+(-1)xy[α(y)，[z，x]]+(-1)yz[α(z)，[x，y]]=0.則稱(L，[，]，α)是Hom-李超代數.

定義1.2[9]設(L，[，]，α)是一個三元組.其中：L為域K上的Z2-階化線性空間；[，]：L×L→L滿足偶雙線性，即[Lθ，Lμ]?Lθ+μ；α：L→L是偶線性映射.若?x，y，z∈hg(L)，有

(-1)zx[α(x)，[y，z]]+(-1)xy[α(y)，[z，x]]+(-1)yz[α(z)，[x，y]]=0，

則稱(L，[，]，α)是Hom-Leibniz超代數.這里(-1)x的x表示x的階化次數.

顯然，Hom-李超代數是特殊的Hom-Leibniz超代數.

定義1.3[9]設(L，[，]，α)是一個Hom-Leibniz超代數.若?x，y∈L，有α([x，y])=[α(x)，α(y)]，則L稱為保積的Hom-Leibniz超代數.

定義1.4[9]設(L，[，]，α)是一個Hom-Leibniz超代數.L的子空間S稱為L的子代數，若[S，S]?S；L的子代數S稱為Hom-子代數，若α(S)?S；L的子代數I稱為T的理想，若[I，L]?I且[L，I]?I.并且，若[I，I]=0，則稱I為L的交換理想.設I是L的非空子集，若Z(L)={x∈L|[x，y]=[y，x]=0，?y∈L}，則稱Z(L)為L的中心.

2 主要結果

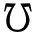
證明由Hom-李超代數定義直接驗證即可.

定義2.1設(L，[，]，α)是一個保積的Hom-Leibniz超代數.次數為θ的線性映射D：L→L若滿足：Dα=αD；[D(x)，αk(y)]+(-1)θx[αk(x)，D(y)]=D([x，y])，?x∈hg(L)，y∈L.則稱其為L的αk-導子，其中k∈N.

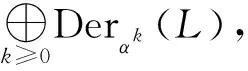
定義2.2設(L，[，])是域K上的Hom-Leibniz超代數，D∈Endθ(L).若存在D′，D″∈Endθ(L)，使得

Dα=αD，D′α=αD′，D″α=αD″，

[D(x)，αk(y)]+(-1)θx[αk(x)，D′(y)]=D″([x，y])，?x∈hg(L)，y∈L，k∈N.

則稱D是L的αk-廣義導子.將αk-廣義導子全體構成的集合記為GDerαk(L)，令

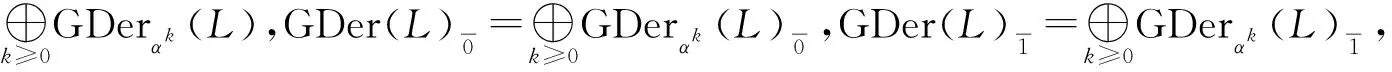
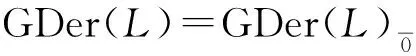
定義2.3設(L，[，])是域K上的Hom-Leibniz超代數，D∈Endθ(L).若存在D′∈Endθ(L)，使得：Dα=αD；D′α=αD′；[D(x)，αk(y)]+(-1)θx[αk(x)，D(y)]=D′([x，y])，?x∈hg(L)，y∈L，k∈N.則稱D是L的αk-擬導子.將αk-擬導子全體構成的集合記為QDerαk(L)，令

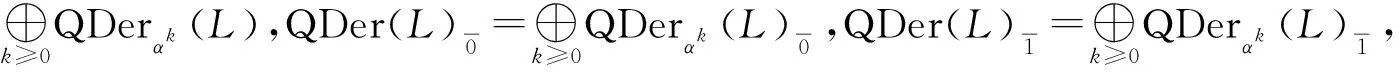
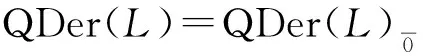
定義2.4設(L，[，])是域K上的Hom-Leibniz超代數，D∈Endθ(L)且

Dα=αD，[D(x)，αk(y)]=(-1)θx[αk(x)，D(y)]=D([x，y])，?x∈hg(L)，y∈L，k∈N.

則稱D是L的αk-中心導子.將αk-中心導子全體構成的集合記為ZDerαk(L)，令

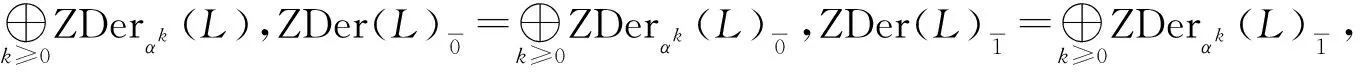
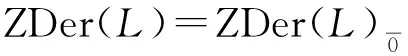
定義2.5設(L，[，])是域K上的Hom-Leibniz超代數，D∈Endθ(L)且

Dα=αD，[D(x)，αk(y)]=(-1)θx[αk(x)，D(y)]=D([x，y])，?x∈hg(L)，y∈L，k∈N.

則稱D是L的αk-型心.將αk-型心全體構成的集合記為Cαk(L)，令

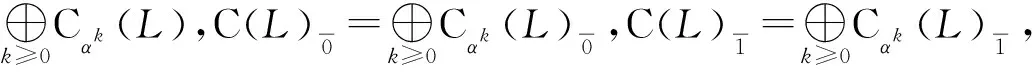
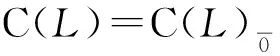
定義2.6設(L，[，])是域K上的Hom-Leibniz超代數，D∈Endθ(L)且

Dα=αD，[D(x)，αk(y)]=(-1)θx[αk(x)，D(y)]，?x∈hg(L)，y∈L，k∈N.

則稱D是L的αk-擬型心.將αk-擬型心全體構成的集合記為QCαk(L)，令

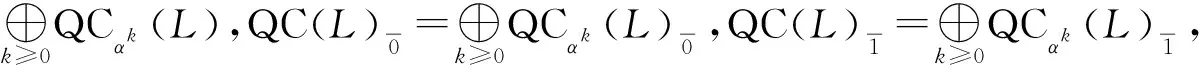
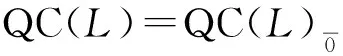
根據以上定義，容易證明

ZDer(L)?Der(L)?QDer(L)?GDer(L)?End(L)，C(L)?QC(L)?QDer(L)?End(L).

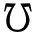
證明(1) 設D1∈(GDerαk(L))θ，D2∈(GDerαs(L))μ.則對?x，y∈hg(L)，有

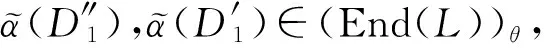
因此?x，y∈hg(L)，

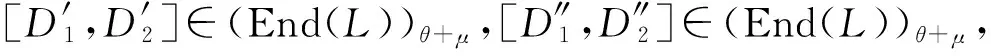
設D1∈Cαk(L)，D2∈Cαs(L).則?x，y∈hg(L)，

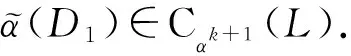
[[D1，D2](x)，αk+s(y)]=[D1D2(x)，αk+s(y)]-(-1)θμ[D2D1(x)，θk+s(y)]=
D1([D2(x)，αs(y)])-(-1)θμD2([D1(x)，αk(y)])=[D1，D2]([x，y]).

同理，

(-1)(θ+μ)x[αk+s(x)，[D1，D2](y)]=[D1，D2]([x，y])s.

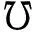
(2) 設D1∈ZDerαk(L)，D2∈ZDerαs(L).則對?x，y∈hg(L)，有

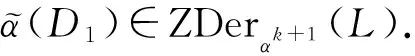
[[D1，D2]([x，y])]=D1D2([x，y])-(-1)θμD2D1([x，y])=
D1([D2(x)，αs(y)]+(-1)μx[αs(x)，D2(x)])=0，

[[D1，D2](x)，αs+k(y)]=[(D1D2-(-1)θμD2D1)(x)，αs+k(y)]=
-(-1)θμ(D2([D1(x)，αky])-(-1)μ(θ+x)[αs(D1(x))，D2(αky)])=
-(-1)μ(θ+x)[D1(αs(x))，αk(D2(y))]=0.

因此[D1，D2]∈(ZDerαk+s(L))θ+μ，從而ZDer(L)是Der(L)的Hom-理想.

命題2.2設(L，[，]，α)是一個保積的Hom-Leibniz超代數，則：(1) [Der(L)，C(L)]?C(L)；(2) [QDer(L)，QC(L)]?QC(L)；(3) [QC(L)，QC(L)]?QDer(L)；(4) C(L)?QDer(L).

證明(1) 設D1∈(GDerαk(L))θ，D2∈(Cαs(L))μ，?x，y∈hg(L).則有

[D1D2(x)，αk+s(y)]=D1([D2(x)，αs(y)])-(-1)θ(μ+x)[αk(D2(x))，D1(αs(y))]=
D1([D2(x)，αs(y)])-(-1)θ(μ+x)[D2(αk(x))，αs(D1(y))]=
D1D2([x，y])-(-1)θ(μ+x)(-1)μx[αk+sk(x)，D2D1(y)]，

且

[D2D1(x)，αk+s(y)]=D2([D1(x)，αk(y)])=
D2D1([x，y])-(-1)θxD2([αk(x)，D1(y)])=
|D2D1([x，y])-(-1)(θ+μ)x[αk+s(x)，D2D1(y)].

因此，

[[D1，D2](x)，αk+s(y)]=[D1D2(x)，αk+s(y)]-(-1)θμ[D2D1(x)，αk+s(y)]=
D1D2([x，y])-(-1)θμD2D1([x，y])=[D1，D2]([x，y]).

另一方面，

[D1D2(x)，αk+s(y)]=D1([D2(x)，αs(y)])-(-1)θ(μ+x)[αk(D2(x))，D1(αs(y))]=
(-1)μx(D1([αs(x)，D2(y)])-(-1)θ(μ+x)[αk+s(x)，D2D1(y)])=
(-1)μx[D1(αs(x))，αk(D2(y))]+(-1)(θ+μ)x[αk+s(x)，D1D2(y)]-
(-1)θμ(-1)(θ+μ)x[αk+s(x)，D2D1(y)]，

[D2D1(x)，αk+s(y)]=(-1)μ(θ+x)[D1(αs(x))，αk(D2(y))]，

則

[[D1，D2](x)，αk+s(y)]=[D1D2(x)，αk+s(y)]-(-1)θμ[D2D1(x)，αk+s(y)]=
(-1)(θ+μ)x([αk+s(x)，D1D2(y)]-(-1)θμ[αk+s(x)，D2D1(y)])=
(-1)(θ+μ)x[αk+s(x)，[D1，D2](y)].

因此[D1，D2]∈(Cαs+k(L))θ+μ，[Der(L)，C(L)]?C(L).

結論(2)的證明同結論(1)的證明類似，此處略去.

(3) 設D1∈(QCαk(L))θ，D2∈(QCαs(L))μ，?x，y∈hg(L).則

[[D1，D2](x)，αk+s(y)]+(-1)(θ+μ)x[αk+s(x)，[D1，D2](y)]=0.

設D′=0，因此[D1，D2]∈(QDerαk+s(L))θ+μ.

結論(4)與結論(1)—(3)的證明類似.

定理2.2設(L，[，]，α)是一個保積的Hom-Leibniz超代數，其中α是滿射，Z(L)是L的中心.則[C(L)，QC(L)]?End(L，Z(L)).特別地，若Z(L)={0}，則[C(L)，QC(L)]={0}.

證明設D1∈(GDerαk(L))θ，D2∈(Cαs(L))μ，?x，y∈hg(L).因為α是滿射，所以?y′∈L，?y∈L使得y′=αk+s(y).則

[[D1，D2](x)，y′]=[[D1，D2](x)，αk+s(y)]=
[D1D2(x)，αk+s(y)]-(-1)θμ[D2D1(x)，αk+s(y)]=
D1([D2(x)，αs(y)])-(-1)μx[αsD1(x)，D2αk(y)]=
D1([D2(x)，αs(y)])-(-1)μxD1([αs(x)，D2(y)])=
D1([D2(x)，αs(y)]-(-1)μx[αs(x)，D2(y)])=0.

同理，

[y′，[D1，D2](x)]=[αk+s(y)，D1D2(x)]-(-1)θμ[αk+s(y)，D2D1(x)]=
D1([D2(y)，αs(x)]-(-1)μx[D2(y)，αs(x)])=0.

因此[D1，D2](x)∈Z(L)，且[D1，D2]∈End(L，Z(L)).特別地，若Z(L)={0}，易知[C(L)，QC(L)]=0.

定理2.3設(L，[，]，α)是一個保積的Hom-Leibniz超代數，α是滿射.若Z(L)={0}，則QC(L)是一個Hom-李超代數，當且僅當[QC(L)，QC(L)]=0.

證明設D1∈(QCαk(L))θ，D2∈(QCαk(L))μ，x∈hg(L).因為α是滿射，則?y′∈hg(L)，存在y∈hg(L)使得y′=αk+s(y).因為QC(L)是Hom-李超代數，則[D1，D2]∈(QCαk+s(L))θ+μ，即

[[D1，D2](x)，y′]=[[D1，D2](x)，αk+s(y)]=(-1)(θ+μ)x[αk+s(x)，[D1，D2](y)].

利用命題2.2，

[[D1，D2](x)，y′]=[[D1，D2](x)，αk+s(y)]=-(-1)(θ+μ)x[αk+s(x)，[D1，D2](y)].

因此[[D1，D2](x)，y′]=[[D1，D2](x)，αk+s(y)]=0，即[D1，D2]=0.

充分性顯然.

[xλ?ti，xθ?tj]=[xλ，xθ]?ti+j，

xλ，xθ∈hg(L)，i，j∈{1，2}是一個Hom-Leibniz超代數.

證明設xλ，xθ，xμ∈hg(L)且i，j，k∈{1，2}，有

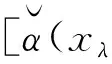
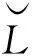
記xt(xt2)=x?t(x?t2).

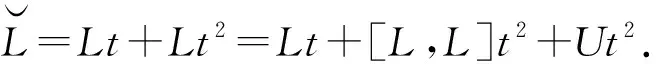
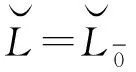
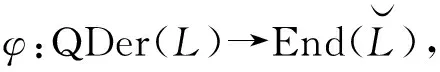
φ(D)(at+bt2+ut2)=D(a)t+D′(b)t2，

其中D′和D滿足定義2.3，a∈hg(L)，b∈hg([L，L])，u∈hg(U)且d(a)=d(b)=d(u).

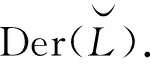
證明(1) 若φ(D1)=φ(D2)，則對任意a∈hg(L)，b∈hg([L，L])和u∈hg(U)，有

φ(D1)(at+bt2+ut2)=φ(D2)(at+bt2+ut2)，

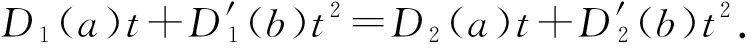
故D1(a)=D2(a)，D1=D2，即φ是單射.

假設存在D″使得

φ(D)(at+bt2+ut2)=D(a)t+D″(b)t2，

[D(x)，αk(y)]+(-1)Dx[αk(y)，D(y)]=D″([x，y])，

則有D′([x，y])=D″([x，y]).因此D′(b)=D″(b).故

φ(D)(at+bt2+ut2)=D(a)t+D′(b)t2=D(a)t+D″(b)t2，

可得φ(D)由D決定.

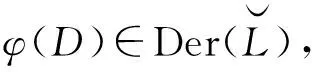
對任意x，y∈hg(L)，有

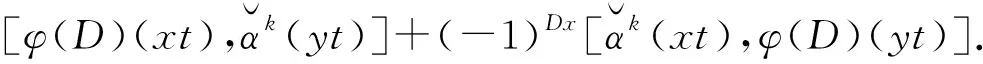
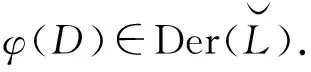
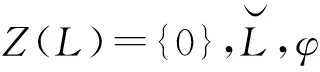
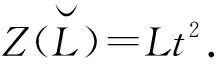
定義映射f：Lt+[L，L]t2+Ut2→Lt2使得

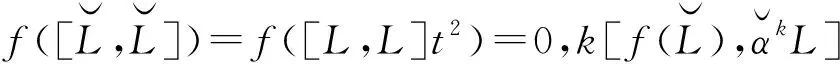
(ɡ-f)(Lt)=ɡ(Lt)-ɡ(Lt)∩Lt2=ɡ(Lt)-Lt2?Lt，(ɡ-f)(Ut2)=0，

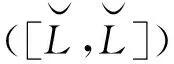
因此存在D，D′∈End(L)，使得?a∈hg(L)，b∈hg([L，L])，有

(ɡ-f)(at)=D(a)t，(ɡ-f)(bt2)=D′(b)t2，

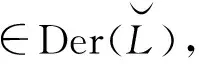
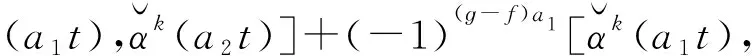
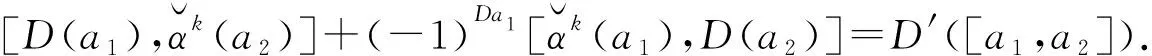
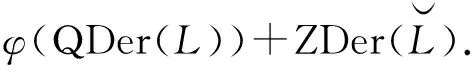
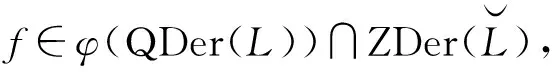
f(at+bt2+ut2)=φ(D)(at+bt2+ut2)=D(a)t+D′(b)t2.