一種基于神經網絡的雙足機器人混合動力學系統辨識方法

吳曉光 張天賜 韋 磊 李艷會 王挺進 張 波

1.燕山大學河北省測試計量技術及儀器重點實驗室，秦皇島，066004 2.中國唐山機車車輛有限公司，唐山，063000

0 引言

隨著雙足機器人技術的發展，高效、穩定、準確的控制策略已成為雙足機器人研究中的重要方向，多種行之有效的控制方法相繼被提出［1?4］，然而上述方法大多建立在機器人系統已知的基礎上。雙足機器人自身固有的變結構、強耦合特性［5］，以及足地碰撞引發的連續與離散混合特性［6］，使得準確建立模型變得非常困難。實現雙足機器人的高效穩定控制，需要構造一個確定的非線性映射來代替原系統，即雙足機器人系統辨識。因此，辨識技術成為機器人不確定系統高效控制中亟待解決的關鍵問題。

為將系統辨識技術有效地應用于雙足機器人的高效控制，研究人員嘗試了多種適宜于復雜非線性系統的辨識方法，如采用最小二乘法［7］、支持向量機［8］、神經網絡［9］來辨識雙足機器人的運動軌跡。在各類型神經網絡中，徑向基函數神經網絡（radial basis function neural network，RBFNN）以其強大的非線性函數逼近能力、自學習適應能力，受到眾多學者的青睞。CAPI等［10］針對不同任務下機器人步態的具體要求，利用RBFNN實現了運動軌跡的辨識，并成功應用于雙足機器人確定步態的行走控制。CHALODHORN等［11］利用RBFNN辨識雙足機器人的逆動力學模型，并基于該辨識模型預測給定位姿下的最優關節轉矩，從而實現機器人的穩定行走。然而，上述研究所采用的辨識方法僅針對主動機器人的連續運動軌跡而忽略了足地接觸碰撞的影響，不能充分表征雙足機器人動力學本質；摒棄了運動過程中步態的多樣性，不適用于步態柔順、自然的混合動力學機器人系統。因此有必要引入一種有效的、針對離散足地碰撞的建模方法作為上述研究的補充，將二者有機結合，實現對雙足機器人動力學本質的更深層次表達。

動態模糊神經網絡（dynamic fuzzy neural network，DFNN）是目前常用的離散系統建模工具之一。DFNN作為一種改進的模糊神經網絡，具有強大的泛化能力與對動態系統的在線辨識與預測能力［12?13］。WU等［14］設計一種 DFNN并應用于非線性離散時間序列的辨識。徐春梅等［15］利用學習速率自適應調整的DFNN，成功實現了動態非線性離散系統的快速辨識與準確預測。因此，可以利用基于DFNN的離散建模方法，對足地碰撞階段進行準確的辨識。此外，混沌步態作為雙足步行中的最為復雜步態表現形式，不僅具有深層次的復雜特性，同時蘊含著深層次的系統動力學特性［16］，因而可將雙足機器人系統的混沌步態作為辨識目標，以充分體現雙足機器人混合系統的動力學特性。

本文針對雙足機器人混合動力學系統的辨識問題，以雙足機器人運動過程中最為復雜的混沌步態作為辨識對象，提出一種基于混沌粒子群優化算法［17］優化的徑向基函數神經網絡（CPSO?RBFNN）和DFNN的雙足機器人混合動力學系統辨識方法。

1 雙足機器人混合動力學系統辨識可行性分析

本文立足于雙足機器人擺動階段與碰撞階段之間存在的變量耦合、轉換關系，從雙足機器人軌道漸進穩定性角度推導該混合系統的整體可辨識條件。

考慮雙足機器人系統擺動階段的微分方程：

其中，x為系統的狀態變量，x∈X；X是Rn中一連通的開子集；u(t)為系統控制輸入，u(t)∈u?Rm；f為不確定參數的光滑非線性函數；g為系統非線性方程。假定：①系統中的所有狀態均可測；②對于任意合理有界初始條件，系統在μ的作用下一致有界；③f、g為連續函數且滿足局部Lip?schitz條件，則式（1）的解x(t)唯一。

R。最后令Φ∶F→Χ。則對于存在碰撞作用的混合動力學模型，有

方程 φ:[t0,tf)→ Χ,tf∈R?{∞},tf＞t0為式（2）的解。如果：

（1）φ(t)在[t0,tf)上右連續；

（2）區間(t0,tf)上任一點的左極限存在；

（3）存在一個閉的離散子集Γ?[t0,∞)；則滿足：

（1）對于任意t? Γ,φ(t)均可微且dφ(t)dt=f(φ (t))+g(φ (t))u(t)；

（2）如果t∈Γ，φ(t-)∈ F且φ(t+)= Φ(φ(t-))，則碰撞時間集為閉集，且僅有一個碰撞點。

若u(t)=0，則式（2）為時不變系統。對任意ε＞0，若O存在一個開鄰域P使得任意p∈P，則式（2）存在一個解φ:[0,∞)→Χ滿足φ(0)=p，并且對于所有t≥0，若滿足二者間距離δ(φ(t),O)＜ε，則周期軌道O為李雅普諾夫穩定。如果O存在一個開鄰域P，使得對于任意p∈P，式（2）存 在 一 個解 φ:[0,∞)→Χ 滿足0，則軌道O是吸引的。如果軌道O既是穩定的，也是吸引的，則軌道O是李雅普諾夫漸進穩定的。

由式（2）可知，碰撞集合F={ |x∈Χ H(x)=0}，其中，H∶Χ→R為連續可微。如果式（1）的解與F交集的閉僅為一個點xˉ∶=Oˉ?F，且道Oˉ穿過F而不是與F相切，其中，Oˉ為軌道O的閉集。

對于存在碰撞作用的時不變雙足機器人系統：

采用龐加萊截面法拓展上述非平凡的周期軌道，使其穿越F，并令φ為滿足x˙=f(x)的解。

為實現這一拓展需作如下假設：①f(x)在Χ上連續；②對于給定的任意初始條件，式（4）的解唯一且連續依賴于初始條件；③存在一個可微的函數H∶Χ→R，使得F={ |x∈ Χ H(x)=0}，連續的，其中，F為源自于X的子集拓撲。

定義碰撞時間函數TI(x0)∶Χ→R?{∞}為

引理1 如果假設①～③成立，則TI在點x0連續，其中，0＜TI(x0)＜ ∞且LfH(φ (TI(x0),x0))≠ 0［18］。

在滿足假設①～④的條件下，取定龐加萊截面為碰撞開始時刻對應的狀態空間，則龐加萊回歸映射P(x)∶=φ(TI(Φ(x)),Φ(x))是連續的。由于x0作為軌道迭代的初值，并且是相軌跡與龐加萊截面的交點，具有唯一性，即x0=Oˉ? ～F，因此可以利用x0作為自變量去映射一整條周期軌道O(Φ (x0))。

引理2 滿足假設①～③時，d∶～X→R在O上連續［18］。

定理1 如果假設①～④均滿足，則下列命題成立：①如果O是式（3）穿越F的周期軌道，則存在點x0∈～F生成O；②當且僅當Φ(x0)生成的周期軌道穿越F時，x0∈～F為P的不動點；③當且僅當軌道O(Φ(x0))是李雅普諾夫穩定的，x0∈～F為xk+1=P(xk)的穩定平衡點；④當且僅當軌道O(Φ (x0))是李雅普諾夫漸進穩定的，x0∈ ～F為xk+1=P(xk)的漸進穩定平衡點［18］。

若O是穿越F的給定周期軌道，且x∈～X，TI(x)，滿足 φ(t-,x)= φ(t,x)。

對于式（2）所表示的雙足機器人系統，g(·):R2n+1→Rn是不確定非線性連續函數。由于g(·)與控制輸入u為連續函數，故上述理論推導同樣適用于式（2）。將第n次足地間碰撞時刻記為tn，碰前碰后時刻分別由tn、t+n表示。對于t∈[0,∞)時刻機器人的步態x(t)，顯然存在自然數n，使得tn≤t＜tn+1。設?為第n次碰撞后到當前狀態的相對時間。令t=?+tn,?≥0，則步態x(t)可以表示為

2 基于CPSO的RBFNN

本文利用CPSO?RBFNN強大的逼近能力與快速學習能力對雙足步行中的擺動階段建模，從而達到對該階段動力學模型的準確辨識。RBFNN一般由輸入層、隱含層和輸出層組成［19］。假設網絡輸入Xn=［xn1xn2… xnm］，實際輸出Yn=［yk1yk2… yks］，那么該網絡的輸入輸出映射關系可表述為

式中，n為訓練樣本數；S為輸出單元個數；I為隱含層節點數；Xi為基函數的中心，Xi=［xi1xi2… xim］∈R1×m；θj為網絡閾值；ωij為網絡連接權值；σ為基寬。

式（9）中的基函數φ為高斯函數，RBFNN的精度主要由中心節點、基寬、閾值等參數決定。

CPSO算法是在粒子群優化（particle swarm optimization，PSO）算法［20］的基礎上發展而來的一種新型群智能仿生優化算法，它在每次迭代尋優的過程中由混沌序列隨機產生若干粒子并映射至原有解空間，從中選取適應度較高的個體替換原有粒子，作為下次迭代的初始種群。該算法能大大增加粒子種群多樣性，避免陷入局部最優值，提升算法在解空間的尋優能力與收斂速度［21］。因此，本文采用CPSO算法對RBFNN的Xi、σ和ωij同時優化，從而得到最優的擺動階段動力學辨識模型。

CPSO?RBFNN訓練主要包括以下幾個步驟：

（1）粒子群參數初始化，主要包括種群規模、最大迭代次數、慣性權重、學習因子、位置和速度取值區間等。

（2）建立RBFNN并生成粒子群，利用混沌序列初始化粒子種群與速度。

（3）計算粒子適應度函數值，對于本文，第i個粒子適應度計算公式為

式中，yk為神經網絡實際輸出值；y^k為期望輸出值；N為種群個數。

計算種群內各個粒子適應度，并把當前種群中適應度最低的粒子位置設置為全局最優位置。

（4）按照標準粒子群算法更新粒子的位置與速度［20］。對于適應度函數值小于種群平均適應度值的粒子，利用Logistic映射進行混沌優化。具體優化過程見文獻［22］。

（5）當迭代次數小于最大迭代次數時，返回步驟（3），否則結束粒子群尋優。將最優粒子解碼后，賦值給RBF中心、基寬向量和網絡權值，得到最優的辨識網絡。

3 動態模糊神經網絡DFNN

在雙足步行中，理想化的碰撞階段可視為單次迭代過程［23］。鑒于機器人混沌步態對初值的敏感性，需尋找一類泛化能力強的神經網絡識別未訓練樣本，以彌補辨識結果的誤差，防止后續迭代中的誤差累計使辨識結果迅速偏離原有混沌軌道。為此，本文采用DFNN來辨識該碰撞階段。該網絡由輸入層、模糊化層、規則層、結論層和清晰化層組成。網絡拓撲結構如圖1所示，其本質是代表一個基于TS模型的模糊系統，其中，x1、x2、…、xr為網絡輸入，y是系統的輸出，Mij是第i個輸入變量的第j個隸屬函數，Rj表示第j條模糊規則，Nj是第j個歸一化節點，wj是第j個規則的結果參數或者連接權，u為系統總規則數。對該網絡更詳細的描述見文獻［14］。

圖1 動態模糊神經網絡結構Fig.1 Structure of dynamic fuzzy neural network

DFNN訓練過程主要包括以下幾個步驟：①選取訓練樣本中的第一組數據作為系統觀測數據，建立系統的模糊規則，得到對應的規則強度。②對高斯隸屬度函數的中心和寬度進行修正，使系統性能指標達到期望值。③依次把訓練樣本中的數據送入DFNN，并重復步驟①、②。利用每次迭代學習的過程，增加有用或者剔除無效模糊規則，不斷修正現有的規則庫，使神經網絡滿足辨識精度要求。當達到最大迭代次數之后，網絡訓練結束。④利用修正的網絡模型去預測碰撞結果，進而實現雙足機器人碰撞階段的準確辨識。整個辨識原理如圖2所示。

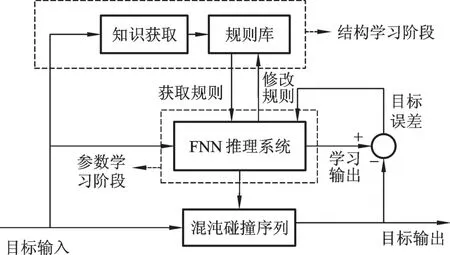
圖2 碰撞階段辨識原理圖Fig.2 Schematic diagram of identification in collision stage

4 聯合辨識算法設計

分別利用CPSO-RBFNN和DFNN對雙足機器人碰撞階段、擺動階段準確辨識后，利用兩階段之間存在的變量耦合、轉換關系，實現對機器人動力學系統的整體辨識與步態預測。聯合辨識算法如下：

（1）設定雙足機器人初始狀態變量；

（2）設定預測步數S0，并令初始步數S=0；

（3）將初始狀態點送入CPSO-RBFNN，辨識擺動階段動力學方程系數矩陣；

（4）利用四階Runge-Kutta思想完成辨識方程求解，求解終止條件為θ1= θ2-2β3；

（5）記錄擺動終止時機器人各狀態變量，送入DFNN得到碰撞后各狀態值；

（6）左右腿角色互換，即θ+1=θ+2和θ+2=θ+1，其中，θ1、θ2分別表示支撐腿與擺動腿角度，上角標“-”和“+”分別表示碰撞瞬間的前后時刻，下同；

（7）判斷是否滿足辨識步數要求，即是否S=S0，若滿足，則算法停止；否則令S←S+1，返回步驟（3）。

5 仿真結果與討論

雙足機器人行走步態主要包括極限環步態、倍周期分岔和混沌步態［24］，其中，混沌步態作為雙足步行中最為復雜的步態表現形式，最能體現雙足機器人動力學系統的復雜本質。若能解決雙足機器人混沌步態的辨識問題，自然能把該方法推廣至其他類型的步態辨識中。因此，本文以兩連桿被動雙足步行機器人所產生的混沌步態為辨識對象來驗證DFNN與CPSO?RBFNN的聯合辨識效果。

5.1 雙足機器人混合動力學模型

本文的雙足被動機器人模型如圖3所示，該模型由2個完全相同的剛性直腿組成，兩腿由髖關節點H相連。模型詳細參數與取值見文獻［18］。

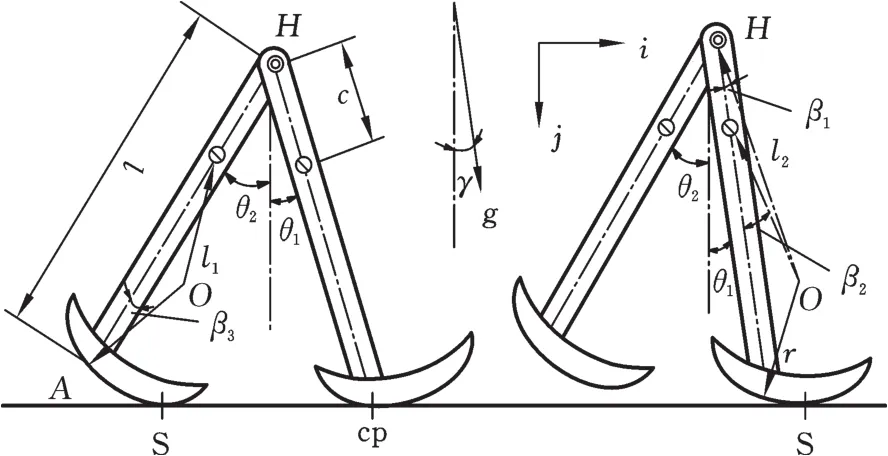
圖3 機器人模型示意圖Fig.3 Model structural diagram of biped robot

在對雙足機器人運動過程做出若干理想化假設后［23］，分別利用拉格朗日法和角動量守恒關系推導運動中擺動階段和碰撞階段模型，得到該模型混合動力學方程：

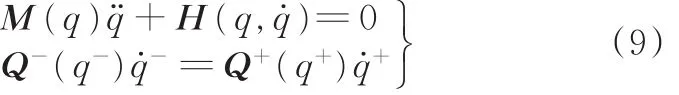
其中，M（q）為2× 2正定質量慣性矩陣；H(q,q˙)為重力、離心力和哥氏力之和；矩陣Q-、Q+由角動量守恒關系得到。

碰撞后兩腿的角色互換，故有

式（9）、式（10）構成了完整的雙足機器人混合動力學模型。

5.2 基于CPSO”RBFNN的擺動階段辨識

為準確描述雙腿運動過程，首先通過調整斜坡傾角γ使機器人呈現混沌步態。利用龐加萊映射的方法，分析機器人步態隨γ變化的情況。取足地碰撞后的瞬間為龐加萊截面，圖4為斜坡傾角γ ∈[0.13,0.172]（rad）時，龐加萊截面上 θ1的分岔圖。由圖4可知，隨著γ的逐漸增加，機器人步態逐漸從單周期過渡到倍周期分岔直至混沌。把圖4中矩形窗口區域進一步放大，可得圖5。由圖 5可知，當γ∈[0.164729,0.172]（rad）時，機器人步態表現為完全混沌。在此，本文利用γ=0.171rad時機器人混沌步態所產生的狀態點列作為CPSO-RBFNN的辨識樣本集。

圖4 龐加萊截面θ1分岔圖Fig.4 The final state diagram ofθ1on the Poincaré section

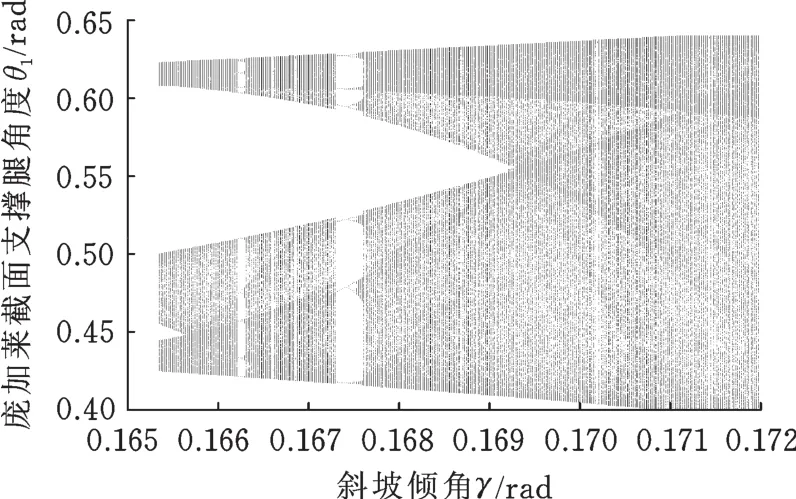
圖5 混沌終態區域Fig.5 Chaotic terminal region

為得到較為豐富的擺動階段神經網絡學習樣本集，從任意合適的初值狀態點開始迭代2萬次，以充分遍歷混沌區域。隨機選取其中5 000組數據點集，并依次代入式（9），得到5 000組擺動方程各項系數點列{M11，M12，M21，M22，H1，H2}，把前 4 500組數據作為訓練樣本集，后500組數據作為測試樣本集。考慮到擺動階段動力學方程中M12=M21且M22為定值，因此確定神經網絡輸入輸出參數集分別為[θ1,θ˙1,θ2,θ˙2]和{M11，M12，H1，H2}。

訓練中，CPSO?RBFNN各項參數取值如下：種群規模n=50，慣性權重w=0.7，學習因子c1=c2=2，最大迭代次數imax=80，神經網絡隱層節點數設為60。圖6所示為適應度函數的收斂過程。神經網絡訓練完成后，利用測試樣本檢驗網絡辨識與預測性能，其中，M11預測誤差曲線見圖 7。取定 [θ1,θ˙1,θ2,θ˙2]=［0.607 6，-1.794 7，-0.607 6，6.081 2］（rad），利用四階Runge-Kutta法完成對辨識所得動力學方程的求解。圖8所示分別為機器人角度與角速度的辨識結果，可見擺動階段辨識結果具有較高準確度。

圖6 適應度曲線Fig.6 Fitness curve

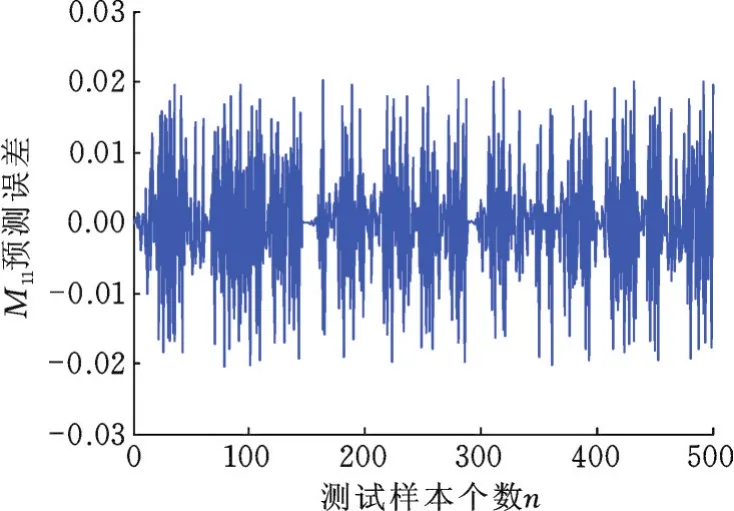
圖7 M11項預測誤差Fig.7 Prediction error ofM11

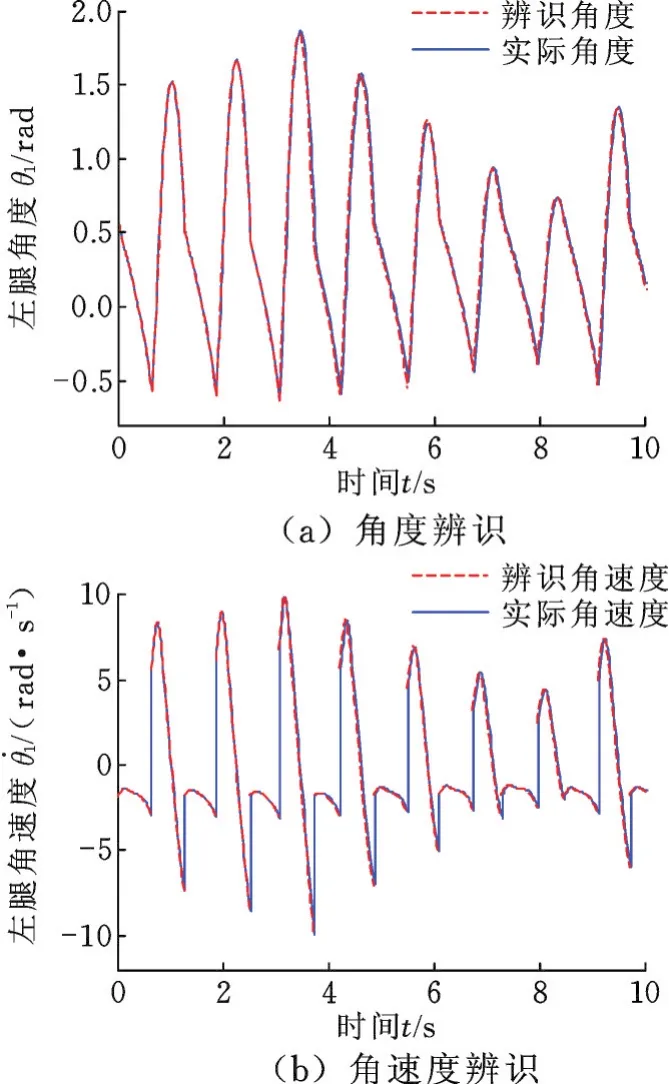
圖8 擺動階段辨識Fig.8 Identification in swing stage

5.3 基于DFNN的碰撞階段辨識

雙足機器人碰撞階段模型描述為x(t+)=Φ(x(t-))，因此碰撞階段可視為單次的迭代。為獲得碰撞階段的辨識樣本，從斜坡傾角γ∈[0.165,0.172]（rad）的范圍中均勻選取 20個值。對于每個斜坡傾角，記錄300個步態周期碰撞后1 000組作為測試集。由于碰撞前后僅角速度產生突變而角度保持不變，因此選取輸入參數集為[θ-1,θ˙-1,θ˙-2]，輸出參數集為[θ˙+1,θ˙+2]。

鑒于雙足機器人碰撞階段對網絡辨識精度具有較高要求，故把學習系統的輸入輸出變量的定義域精細劃分為9個區間。以θ-1為例，圖9表示θ-1的初始隸屬函數曲線與學習后的修正隸屬函數曲線。圖10所示為學習后輸入輸出變量的映射關系。訓練后的神經網絡輸入輸出變量的隸屬函數模糊標記為9個，分別用阿拉伯數字2～8表示，其中，1表示最小，9表示很大，最終得到的模糊規則如表1所示。

圖10 輸入-輸出變量學習后的映射關系Fig.10 Mapping relationship of input”output variables after learning

表1 自適應學習后模糊規則與其隸屬函數Tab.1 Fuzzy rules and its membership function after self-adaptive learning

5.4 聯合辨識

在分別獲得了機器人行走步態碰撞階段、擺動階段的高精度辨識后，將兩個階段進行結合，采用第4節的聯合辨識算法，實現對機器人混沌步態的完整辨識。

為驗證聯合辨識算法的有效性與精確度，同樣選取斜坡傾角γp=0.171rad下的混沌步態作為辨識目標。由圖11可知，在雙足機器人初始行走的10步內，辨識步態幾乎完全匹配混沌步態。10步之后的混沌步態辨識中，由于每次迭代過程中的誤差累計，辨識精度會逐減降低，但辨識軌跡仍然緊緊跟隨混沌軌道，直至20步左右，仍然具有較高準確度，體現出該辨識方法的有效性。

6 結論

雙足機器人是一個高度非線性的混合動力學系統，對雙足機器人系統的準確辨識顯得尤為困難。本文提出一種基于CPSO-RBFNN與DFNN的聯合辨識方法，針對雙足機器人行走過程中連續擺動階段與離散碰撞階段所具有的不同特點，充分發揮神經網絡對復雜非線性系統的逼近能力來擬合雙足機器人系統。仿真結果表明，該方法能夠充分表征雙足機器人系統的動力學特性，準確辨識和預測出雙足步行運動中的混沌步態，從而為基于步態預測的控制方法提供一條新的思路。

圖11 混沌步態辨識曲線Fig.11 Identification of chaotic gait