基于GPU加速策略的稀疏反演表面多次波壓制方法
張文武, 劉玉敏, 楊建華, 張晟瑞, 王 程, 白玉勝, 石 穎
( 1. 東北石油大學 地球科學學院,黑龍江 大慶 163318; 2. 東北石油大學 電氣信息工程學院,黑龍江 大慶 163318; 3. 大慶鉆探工程公司 地球物理勘探一公司,黑龍江 大慶 163357; 4. 中國石油集團測井有限公司 生產測井中心,陜西 西安 710201 )
0 引言
常規的表面多次波壓制方法有兩種[1]:濾波法和基于波動方程的預測相減法。濾波法利用一次波與多次波的可分離性壓制多次波[2-6],對于復雜構造的地震數據,一次波和多次波的可分離性低,不能有效保護有效信號。基于波動方程的預測相減法以地震物理學為基礎,包含多次波預測和自適應相減兩部分,能夠適應復雜地質構造[7-9],但是自適應相減部分存在傷害有效信號的風險[10-13]。
稀疏反演法建立在與反饋迭代法相同的理論基礎上,通過迭代反演方式估計震源子波和地下一次波脈沖響應,進而重構一次波和多次波[14],省去自適應相減部分,可以更好地保護有效信號。Vanborselen R G等提出參數反演方法,在震源子波已知和能量最小的約束條件下估計一次波[15];Biersteker J假設一次波能量最小,利用二維反褶積法估計缺失的淺層有效信號[16];Amundsen L利用上、下行波場的多維除法估計一次波,雖然不需要已知震源子波信息,但需要直達波信息,特別是近偏移距的直達波信息[17];Wang Y利用基于顯式矩陣的反演方法估計有效波,可以消除由近偏移距缺失導致的壓制效果不理想,但包括多次波預測和自適應相減兩部分[18];Berkhout A J在逆數據域估計一次波和多次波,省去自適應相減部分[19],但大量的矩陣求逆運算存在反演風險[20];Herrmann F J等在曲波域估計一次波,需要預測的多次波指導分離過程[21]。在SRME(Surface-Related Multiple Elimination)理論基礎上,Groenestijn G J A V等提出基于稀疏反演估計一次波的方法(EPSI, Estimation of Primaries by Sparse Inversion),可以避免對有效波的損傷[14,22],但高計算成本是制約EPSI方法發展的主要因素。
基于CUDA架構的GPU加速技術在處理矩陣運算方面優勢明顯,廣泛應用于地震數據處理方面[23-25]。為解決EPSI方法大量的矩陣運算,筆者在傳統的GPU加速方法的基礎上進行改進,實現所有頻率成分的同步運算,并減少主機端和設備端的數據傳輸,相比傳統GPU加速的EPSI方法和常規EPSI方法,計算效率更高。
1 EPSI方法原理
根據Rayleigh Ⅱ積分和數據矩陣的概念[9],接收到的上行總波場的單頻表達形式為
P=X0S+X0R-P,
(1)
式中:P為接收的上行總波場;X0為一次波脈沖響應;S為震源特性;R-為地表反射系數。對于海洋數據,R-=-1,X0和S的乘積為有效波P0(不在自由表面發生反射的波,包括一次波和層間多次波)。X0、R-和P三者的乘積為自由表面多次波M。不同于SRME方法,EPSI方法不引入自適應算子A,直接把X0和S作為未知量,通過不斷迭代反演估計兩者的值。盡管假設反射系數R-=-1,但式(1)的未知量(X0和S)多于已知量(P),為欠定方程,有多解,需增加約束條件:(1)一次波脈沖響應X0在時間域是稀疏的;(2)忽略震源的方向特性。
式(1)可看作一個反演過程,通過依次求取X0和S,使接收的地震記錄與估計的地震記錄的殘差能量最小。目標函數[26]可表示為
(2)
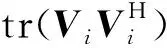
利用最速下降法,經過多次迭代得到X0和S。由于X0和S相互獨立,整個過程可分為兩部分:(1)固定S,更新X0;(2)固定X0,更新S。EPSI方法的全部過程為
(1)設X0和S的初值為0。

(3)對ΔX0進行稀疏約束:
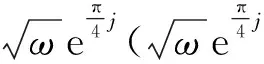
2)變換到時間域,采用合適的時窗(隨迭代次數的增加而增大,可以加快收斂速度),選取每道振幅的最大值。

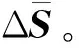
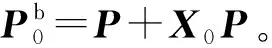
2 基于GPU加速策略的EPSI方法
EPSI方法存在大量矩陣運算,耗費大量時間。GPU加速技術在處理矩陣這類并行度高、密集型強的浮點方面運算優勢明顯,因此被廣泛應用于地震數據處理[23-25]。將GPU加速策略應用于EPSI方法,可

圖1 傳統GPU加速方法的計算流程Fig.1 Flow chart of traditional acceleration strategy
以提高計算效率,降低計算成本。
CUDA是NVIDIA推出的通用并行計算架構,作為一種運算平臺,可以用C語言寫出在顯示芯片上執行的程序,不需要學習特定的顯示芯片指令和特殊結構。GPU加速方法的過程為主機端(CPU及系統的內存)的數據導入設備端(GPU及其顯示內存),在設備端運行核函數[27],將運行的結果導回主機端。
在傳統的GPU加速方法基礎上,提出一種新的GPU加速策略。
傳統GPU加速方法的計算流程為:(1)將x-t域地震數據在時間方向進行傅里葉變換,得到x-ω域數據。(2)抽取單頻成分數據導入設備端。(3)在設備端完成矩陣運算。(4)將運算結果導回到主機端。(5)進行下一頻率成分數據的運算,重復步驟(2-4),直至所有的頻率成分計算結束。以求取一次波脈沖響應X0的搜索步長為例,傳統GPU加速方法的計算流程見圖1。其中,有_SF的表示抽取單頻后的數據,有_d的表示設備端的數據,ω0表示選取的初始頻率,ωmax表示截止頻率。
EPSI方法的不同頻率成分之間的矩陣運算相互獨立、互不相關,因此在理論上可以同步進行。基于傳統GPU加速策略的EPSI方法,沒有實現不同頻率成分矩陣運算的同步進行,除初始頻率成分的計算外,其他頻率成分的計算需要等待之前的所有頻率成分的計算結束后才能進行,在很大程度上影響算法的計算效率。另外,得到的所有的中間結果需要導回主機端,若它們再次參與計算,仍然需要從主機端導入設備端,中間結果在主機端和設備端之間傳導耗費大量的時間。
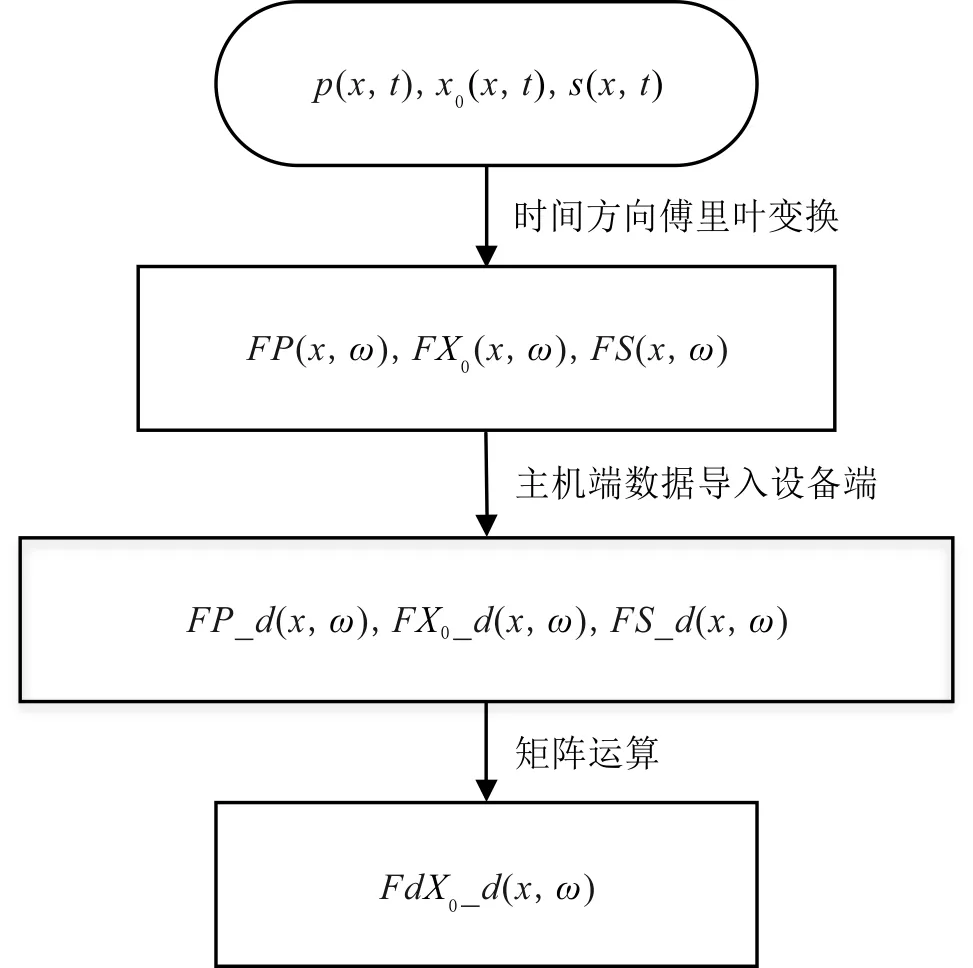
圖2 新的GPU加速策略的計算流程Fig.2 Flow chart of new acceleration strategy
在對傳統的GPU加速方法改進后,提出一種新的GPU加速策略,以求取一次波脈沖響應X0的搜索步長為例,計算流程見圖2。該策略相比于傳統GPU加速方法的優點:(1)所有頻率成分整體導入的耗時較抽取單頻導入耗時少。(2)可實現多個頻率成分運算的同步進行。(3)得到的中間結果除部分必須導回主機端完成運算外,其他的中間結果直接存儲于設備端,減少數據在主機端和設備端之間的傳導。由于設備端的存儲空間有限,當數據體較大、設備端的存儲空間不能保存所有中間變量時,需引入多卡GPU的編程策略,處理大的數據體分塊,每個卡完成部分數據的運算,減輕單卡的存儲負擔,提高新的GPU加速策略的適用性[26]。
3 數據測試
3.1 水平層狀模型測試
實驗模型為單層水平層狀介質,正演得到的地震記錄有200炮,每炮200道接收,空間方向采樣間隔為10.0 m,時間方向1 000個采樣點,采樣間隔為4 ms,包含兩階多次波。采用EPSI方法,得到不同迭代次數估計的一次波單炮記錄(見圖3)。由圖3可知,隨迭代次數增加,一次波同相軸由淺到深被估計出來。抽取該單炮記錄的某一道進行對比分析(見圖4),EPSI方法估計的一次波和多次波的曲線與真實的曲線幾乎重合。

圖3 水平層狀模型不同迭代次數估計的一次波的單炮記錄Fig.3 Single-shot record of estimated primary of horizontal layered by different iterations
3.2 SMAART模型測試
對構造相對復雜的SMAART模型進行測試。地震記錄有200炮,每炮200道接收,空間方向采樣間隔為22.9 m,時間方向626個采樣點,采樣間隔為8 ms。采用EPSI方法,得到不同迭代次數的單炮記錄(見圖5)。由圖5可知,隨迭代次數增加,一次波的同相軸由淺到深被估計出來,擬合殘差逐漸減小。抽取該單炮記錄的某一道進行分析(見圖6),EPSI方法估計的一次波和多次波的曲線與真實的曲線幾乎重合。

圖4 水平層狀模型單道記錄Fig.4 Single-trace record of horizontal layer model


圖5 SMAART模型不同迭代次數估計的一次波的單炮記錄Fig.5 Single-shot record of SMAART model in different iterations

圖6 SMAART模型單道記錄Fig.6 Single-trace record of SMAART model
EPSI方法壓制多次波前后的零偏移剖面的結果見圖7,其中箭頭標記處表明EPSI方法能夠有效的壓制多次波。EPSI方法與SRME方法壓制多次波后的結果的局部放大(2.2~2.6 s)見圖8。由圖8可知,采用EPSI方法壓制多次波后同相軸更加連續,可以更好地保護有效信號。

圖7 EPSI方法壓制多次波前后零偏移距剖面Fig.7 Zero-offset profiles before and after multiple suppression by the EPSI method

圖8 EPSI和SRME方法壓制多次波后的零偏移距剖面的局部放大Fig.8 Zoomed-in sections of zero Offset profile after multiple supression by EPSI and SRME methods
3.3 加速比測試
分別用常規EPSI方法、基于傳統GPU加速的EPSI方法和基于新GPU加速策略的EPSI方法,處理SMAART模型的地震記錄,迭代30次計算耗時見圖9。其中:CPU表示常規EPSI方法;GPU_Global表示存儲器為全局存儲器的、基于傳統GPU加速的EPSI方法;GPU_Share表示存儲器為共享存儲器的、基于傳統GPU加速的EPSI方法;GPU_New表示基于新GPU加速策略的EPSI方法。由圖9可知,基于新GPU加速策略的EPSI方法的計算效率較常規EPSI方法的計算效率提升11倍,較基于傳統GPU加速的EPSI方法提升4倍;不同存儲器類型的、基于傳統GPU加速的EPSI方法的運行時間幾乎相等。通常情況下,存儲器為共享存儲器的運算速度是存儲器為全局存儲器的運算速度的2倍,由于數據傳輸的時間遠遠大于在設備端計算的時間,因此兩種方法總計算耗時相似。

圖9 不同方法的計算耗時Fig.9 Time cost of different methods
以SMAART模型為例,根據基于新GPU加速策略的EPSI方法和常規EPSI方法的運行結果,驗證前者正確性。兩種方法估計的一次波單炮記錄見圖10。由圖10可知,兩種方法估計一次波的同相軸形態和位置幾乎一致。兩種方法估計的一次波頻譜見圖11。由圖11可知,兩者頻譜曲線幾乎重合。兩種方法估計的一次波單道見圖12。由圖12可知,兩種方法的單道曲線形態幾乎一致,表明新GPU加速策略的EPSI方法正確有效。
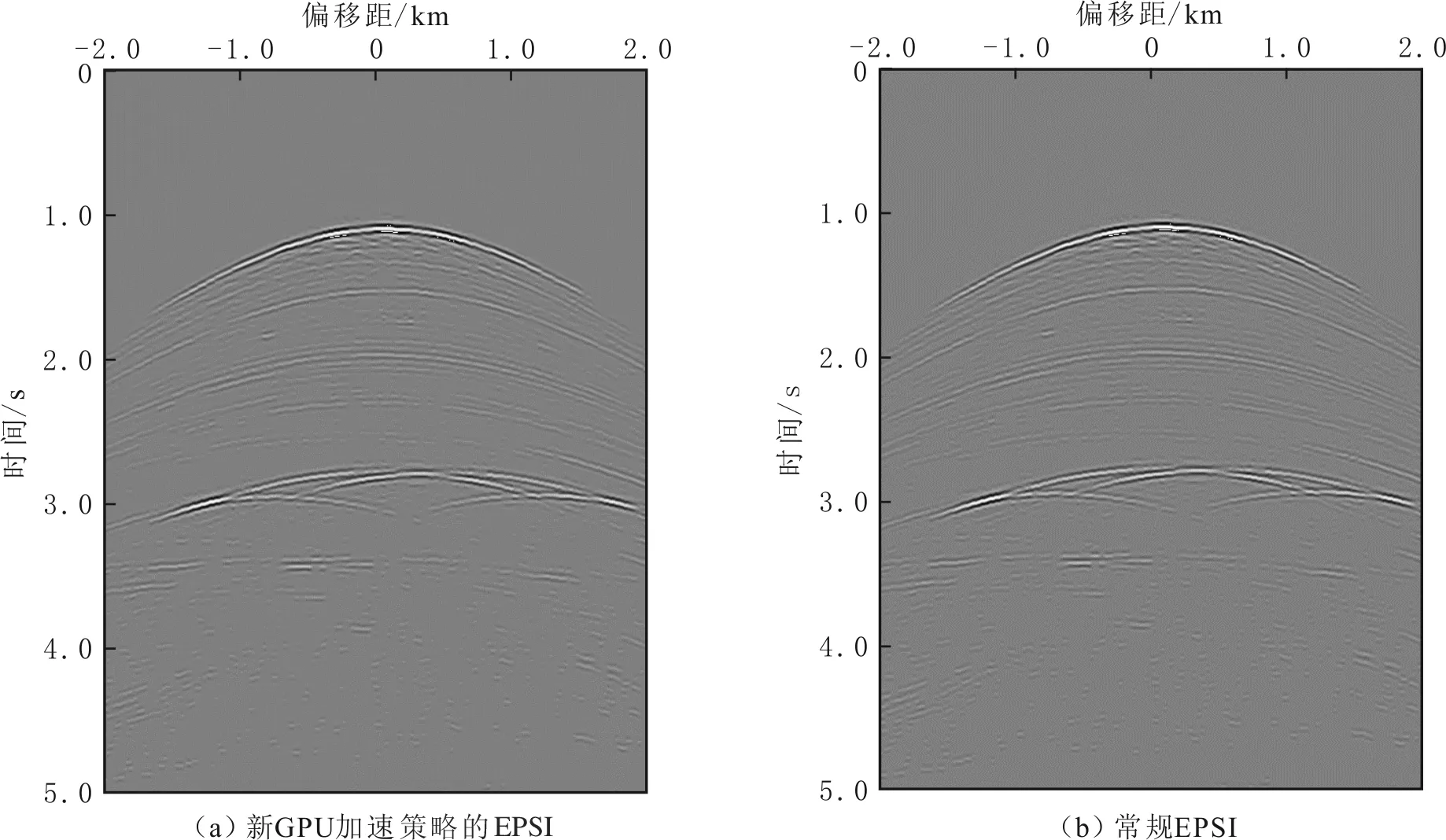
圖10 兩種方法估計的一次波單炮記錄Fig.10 Single-shot record of estimated primary by two methods

圖11 兩種方法估計的一次波頻譜Fig.11 Spectrum comparsion of the estimated primary by two methods
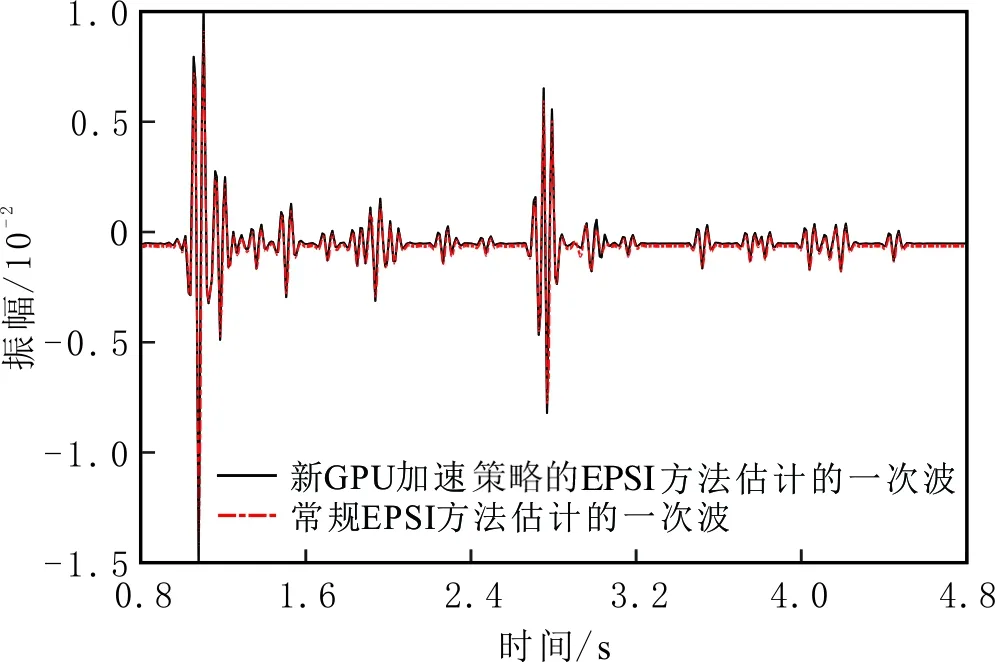
圖12 兩種方法估計的一次波單道記錄Fig.12 Single-trace record of the estimated primary by two methods
4 結論
(1)基于新GPU加速策略的EPSI方法將所有頻率成分整體導入設備端,并將中間結果存儲于設備端,實現所有頻率成分的同步運算,減少主機端和設備端的數據傳輸時間,相比于傳統GPU加速的EPSI方法,計算效率更高。
(2)SMAART模型測試結果表明,基于新GPU加速策略的EPSI方法的計算結果正確有效,可以應用于地震資料的表面多次波的壓制。

