熱電偶分數階傳遞函數階次和參數估計

李文軍， 王瀟楠， 鄭永軍

(中國計量大學 計量測試工程學院, 浙江 杭州 310018)

0 引言

熱電偶被廣泛應用于工業測量領域。隨著工業測量技術水平的提高，測量瞬態溫度的需求也日益迫切和廣泛[1-2]。在已有的測量瞬態溫度方法中，常用的方法是利用多偶組合實現補償式瞬態測溫，以及利用實驗建模技術近似得到系統模型實現瞬態測溫。

Enrico等[3]從理論和實驗兩個角度，對3個溫度傳感器組合測量瞬態溫度和進行動態校準做了對比，討論了產生精確溫度梯度的問題以及保持均勻穩定溫度場的問題。吳朋等[4]對于鎧裝熱電偶傳感器測量瞬態溫度問題，采用支持向量機方法辨識建模，結合量子遺傳算法對核函數參數進行優化以減小建模誤差，對鎧裝熱電偶傳感器測量瞬態溫度做精度補償。Villafae等[5]借助計算流體動力學，用數值實驗方法描述了熱電偶內部熱擴散的演化過程，分析了外部特定測量環境下動態測量誤差的產生原因。Doghmane等[6]采用激光器對K型熱電偶測量接點產生激勵并獲得熱電偶的響應，分別利用Yag激光器加熱獲得熱電偶在單位脈沖激勵下的響應，利用Argon激光器加熱獲得熱電偶在周期性激勵下的響應。郝曉劍等[7]針對鎧裝K型熱電偶動態響應誤差補償，采用CO2激光器加熱產生激勵，并引入紅外探測器做輔助測量，獲得熱電偶的頻率特性對熱電偶進行補償。楊慶濤等[8]針對高超聲速飛行器地面試驗中測量壁面溫度的需求，建立了熱電偶傳感器有限元數值模型，通過傳感器內部傳熱計算，考慮溫差項和儲能項，分析了熱電偶響應特性。上述工作在分析熱電偶動態特性時，都采用了1階或2階整數階傳熱模型，而整數階導熱模型中的時間導數由局部極限定義，表示溫度在某時刻的變化，無法表征整個溫度的變化歷史。

從熱電偶與被測介質之間的傳熱過程看，由于熱電偶測量接點存在熱慣性，且接點與被測介質之間存在接觸熱阻和復雜換熱[9]，測量接點與熱電偶偶絲之間也存在熱量傳遞[10]，故熱電偶測量瞬態溫度的過程構成了一個物理上的延遲過程或者叫做遺傳過程[11]。根據分數階微積分理論，分數階微積分具有記憶特點[12]，采用分數階微積分建立模型能更準確地描述過程的動態特性[13-14]。

本文利用分數階微積分建立了熱電偶偶絲的時間分數階導熱模型，描述了露端式熱電偶測量接點與被測介質之間的換熱過程。給出了測量固體介質表面的瞬態溫度時模型參數的理論值，利用實驗系統采集了熱電偶輸入和輸出。最后通過實驗數據建模，用改進隨機數直接搜索法對傳遞函數的參數以及階次進行了估計。

1 熱電偶時間分數階熱傳導模型

1.1 分數階微積分定義和分數階拉普拉斯變換

(1)

式中：f(t)為t的函數；Γ(·)為Γ函數；n為大于μ的最小整數；τ為被積變量。

設算子下限a=0，對于零初始狀態，Riemann-Liouville分數階微積分對應的拉普拉斯變換為

(2)

式中：L表示拉普拉斯變換；s為拉普拉斯算子；F(·)為s的函數。

(3)

(1)式、(2)式和(3)式給出了分數階微積分算子和對應的拉普拉斯變換。

1.2 熱電偶半無限固體傳熱模型

熱電偶由一對有共同接點的材料互異的熱電偶偶絲組成，如圖1所示。圖1中，熱電偶偶絲的直徑為d，熱電偶偶絲1與熱電偶偶絲2之間存在一個夾角[16]。

由于熱電偶偶絲長度相對于其直徑而言很長，且兩根熱電偶偶絲之間相互絕熱，單根熱電偶偶絲導熱可以視為半無限固體導熱問題[17]。熱電偶偶絲的半無限固體導熱模型如圖2所示，圖2中：q(t)為熱流密度(W/m2)；x為發生熱傳導方向上的長度(m)；Ts(t)為半無限固體溫度分布函數T(t,x)在x=0處的特例。

熱電偶偶絲的導熱視為半無限固體導熱，其熱傳導方程為

(4)

式中：c為熱電偶偶絲材料比熱(J/(kg·K))；ρ為熱電偶偶絲材料密度(kg/m3)；k為導熱系數(W/(m·K))；T0為初始狀態溫度(K)。

引入過余溫度θ(t,x)=T(t,x)-T0，并代入(4)式，得到：

(5)

(6)

當x→-∞， (6)式的邊值解為

(7)

(7)式對x微分并取x=0，有

(8)

根據(2)式和(3)式，對(8)式做分數階拉普拉斯反變換，得到時間分數階微分形式的關系式為

(9)

根據所定義的過余溫度，有

θ(t,0)=T(t,0)-T0=Ts(t)-T0.

(10)

將(10)式代入(9)式并整理得到：

(11)

(11)式等號左側即熱流密度q(t)：

(12)

再定義熱擴散系數α(m2·s)：

(13)

并記熱電偶測量接點溫度與初始狀態溫度的差Tb(t)=Ts(t)-T0，則(11)式化為

(14)

(14)式給出了半無限固體傳熱模型下熱電偶偶絲熱流密度與溫度的時間分數階微分關系式。

1.3 露端式熱電偶測量接點的傳熱方程

當利用露端式熱電偶測量介質溫度時，傳熱過程如圖3所示，圖3中：Tg(t)為被測介質溫度與初始狀態溫度的差；Qi(t)為被測介質到露端式熱電偶測量接點的熱流量；Q1(t)和Q2(t)分別為熱電偶偶絲1、熱電偶偶絲2的熱流量；A1、k1、α1分別為熱電偶偶絲1的截面積、導熱系數和熱擴散系數；A2、k2、α2分別為熱電偶偶絲2的截面積、導熱系數和熱擴散系數。

根據(14)式，分別有

(15)

(16)

露端式熱電偶測量接點的換熱方程表示[18]為

(17)

式中：h為熱電偶測量接點與被測流體之間的換熱系數(被測介質為流體)或者接觸系數(被測介質為固體)(W/(m2·K))；A為熱電偶測量接點與被測物體之間的接觸面積(m2)；m為熱電偶測量接點質量(kg)。

(17)式做拉普拉斯變換并整理，得到：

(18)

(18)式給出了熱電偶時間分數階模型下的傳遞函數，其中s的階次μ1、μ2分別為1.0和0.5，它是一種固定階次的分數階傳遞函數。由于熱電偶在到達穩態溫度過程中，并不是一個嚴格的絕熱過程，s的階次μ1、μ2之間并不一定存在嚴格比例關系[19]，傳遞函數可表示為更一般的形式：

(19)

式中：參數a1為瞬態傳熱過程中測量接點熱慣性引起的延遲；a2為瞬態傳熱過程中溫度激勵引起的熱擴散中單相延遲[20]，也就是熱流梯度相比溫度梯度的延遲；a3為常數項。

2 傳遞函數參數的理論區間

2.1 熱電偶的熱物性參數和幾何參數

對于(19)式，在μ1=1.0和μ2=0.5時，參數a1、a2的理論值可表示為

(20)

(21)

在被測介質溫度變化幅值較小時，測量接點的導熱系數、密度和比熱k、ρ、c都可近似視為常數[21]。以一種常用的鎳鉻- 鎳硅熱電偶為例，表1給出了熱電偶偶絲的熱物性參數。

表1 熱電偶偶絲的熱物性參數

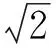
表2 熱電偶測量接點的等效熱物性參數

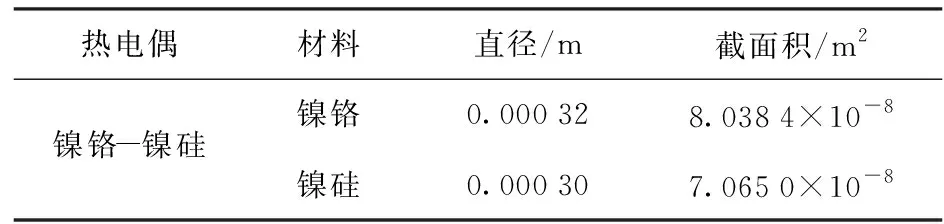
表3 熱電偶偶絲的幾何參數

表4 熱電偶測量接點的等效幾何參數

2.2 固定階次分數階模型參數的理論區間

熱電偶測量接點與被測固體表面的接觸可以簡化為常壓下間隙介質為空氣的金屬表面間接觸[24]，其接觸系數h理論值介于1 000 W/(m2·K)與5 000 W/(m2·K)之間[25]。根據(20)式，并代入表2中熱電偶測量接點熱物性等效參數和表4中熱電偶測量接點幾何等效參數以及接觸系數理論值，得到a1的理論值區間。根據(21)式并代入表1中熱物性參數和表3中幾何參數以及接觸系數理論值，得到a2的理論值區間。計算結果見表5.

表5 參數的理論值

雖然理論值存在誤差，但是當利用改進隨機數直接搜索法等方法估計參數時，上述理論值仍然提供了計算所必須的初始值取值區間。

3 實驗系統和實驗數據

3.1 實驗系統

為了獲得熱電偶在溫度激勵下的動態響應，建立了一種實驗系統，結構如圖4所示，主要包括計算機、美國Measurement Computing公司生產的MCC-USB-2408數據采集卡、日本歐姆龍公司生產的CPM1A可編程控制器、機械往復運動機構以及寧波元創機電公司生產的M12 NPN激光對射開關和日本安立公司生產的ACSⅡ-2000溫度標準源恒溫面。

實驗原理是將熱電偶固定在運動機構上，由可編程控制器控制運動機構，驅動熱電偶進入定位點，使得熱電偶測量接點與恒溫面接觸并保持，熱電偶與恒溫面的接觸時間用激光對射開關采集，熱電偶輸出信號由數據采集卡采集和記錄。實驗中先對熱電偶做靜態響應標定，再參考溫度傳感器動態響應校準規程，最后用實驗系統獲得熱電偶在激勵下的輸出。

3.2 實驗數據

實驗設定的激勵溫度區間設定為300～400 K之間，表6給出了實驗時的3組實驗配置數據。

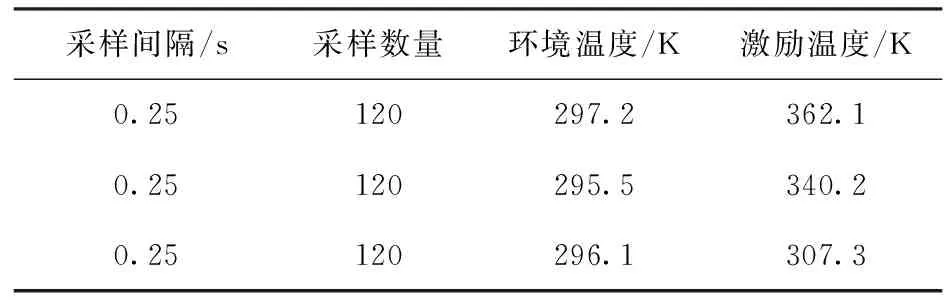
表6 實驗配置

表6的實驗配置對應實驗數據集散點圖如圖5所示。數據集時間步長為0.25 s.

對3組數據做歸一化處理并平均，取激勵發生時間點為起始時間，截取后的數據集長度為101，測量值平均值的散點圖如圖6所示。

上述測量值的平均值可作為待辨識數據集。為了簡便，以下討論中測量值的平均值仍用測量值指代。

4 熱電偶分數階傳遞函數辨識

4.1 分數階傳遞函數的辨識方法

分數階傳遞函數的辨識方法有多種，其中改進Luus-Jaakola算法是Luus-Jaakola算法的優化，它是一種基于隨機搜索的優化方法[26]。采用這種方法，首先在參數搜索區間內采用隨機搜索的方式獲取區間次優值；然后在次優值的基礎上自適應改變搜索區間，做下一步隨機搜索，最終達到最優結果。這種方法的關鍵步驟是采用一個可變收縮系數，在每次迭代后，用收縮系數縮小搜索空間以減少搜索時間并達到搜索目標。改進Luus-Jaakola算法的步驟如下：

1)輸入要搜索的向量β(模型參數和階次)；

2)確定評估函數J；

3)產生隨機搜索向量初始值β0；

4)迭代計算，直到誤差滿足要求或者迭代次數達到限定值；

5)選擇收縮系數φ，將搜索區間乘以收縮系數；

6)反復迭代到滿足評估函數J所確定的性能指標；

在本文算例中，評估函數J采用輸出誤差平方和形式[27]為

(22)

式中：M為數據集長度；y為預報值；y0為測量值；i為離散時間變量，i=0，1，2，…，M.

4.2 改進Luss-Jaakola算法的驗證

為了驗證改進Luss-Jaakola算法，首先對于已知的模型結構進行辨識。假設已知模型為

(23)

根據文獻[28]提出的Luss-Jaakola算法驗證方法，首先由(23)式生成真實值數據集，并增加高斯分布的隨機噪聲，得到一組模擬測量值數據集；然后根據模擬測量值數據集，用改進Luss-Jaakola算法進行辨識，得到參數和階次的辨識結果。

上述驗證算例中，生成的模擬測量值數據集離散時間步長為0.125 s，數據集長度為201. 定義待搜索參數a1、a2、a3和階次μ1、μ2構成的向量為

β=[a1a2a3μ1μ2],

向量真實值為

β=[1.20 1.30 1.00 2.10 0.50],

辨識結果如表7所示。表7中真實值為已知模型給出的參數和階次，估計值為通過模擬測量值辨識得到的參數和階次。

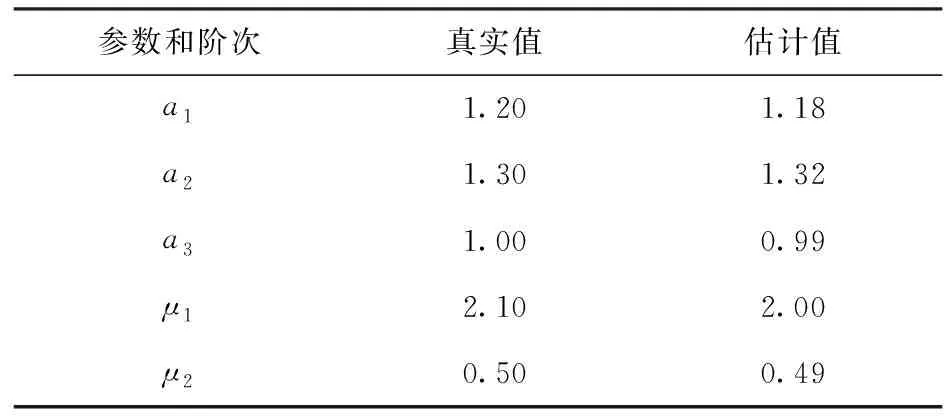
表7 參數真實值和估計值

輸出的模擬測量值、分數階模型估計值和真實值的比較如圖7所示，評估函數J為0.041.

從表7和圖7可以看到，Luaas-Jaakola算法的辨識結果較好地逼近了真實值，表明方法有效。

4.3 固定階次分數階傳遞函數參數的辨識

圖7所示的測量值數據集，其時間步長為0.25 s，數據集長度為101. 根據(19)式，模型階次已經確定，是一種呈比例階次的分數階結構，其形式為

(24)

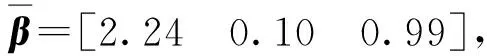
(25)

式中：參數a1為2.24，位于理論值區間[0.48, 2.38]內，表明在固定階次模型下，引入的測量接點熱慣性項與理論估計較為一致，能夠刻畫熱慣性引起的延遲；參數a2為0.10，偏離了理論值區間[0.14, 0.72]，小于理論值區間的最小值0.14，表明在固定階次模型下，引入的熱電偶絲熱擴散項與理論估計不一致，雖然表征了熱電偶絲熱擴散引起的延遲，但是只是延遲的一種弱化表示。輸出測量值和固定階次模型估計值的比較如圖8所示。

從圖8可以看出，固定階次分數階模型在時間軸0～4 s區間時與實驗數據不能很好地吻合。從物理過程分析，0～4 s區間內，激勵溫度與環境溫度差較大，熱電偶測量接點熱物性參數和幾何參數本身也在隨溫度變化而變化，因此參數a1和a2并不是定值，這使得分數階模型在這個時間區間內與測量值之間仍存在較大誤差。

4.4 變階次分數階傳遞函數參數和階次的辨識

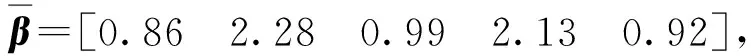
(26)

式中：參數a1和μ1組成項即0.86s2.13項，以及參數a2和μ2組成項即2.28s0.92項，組合表示了測量接點熱慣性和熱電偶偶絲熱擴散所引起的延遲。輸出測量值和變階次模型估計值的比較如圖9所示。

從圖9可以看出，變階次分數階模型在時間軸0～4 s區間與實驗數據能較好地吻合。

4.5 固定階次模型和變階次模型擬合結果比較

圖10是輸出測量值、固定階次模型估計值與變階次模型估計值的比較，其中固定階次模型的評估函數J為0.043，變階次模型的評估函數J為0.020.

從圖10可以看到，變階次分數階模型克服了固定階次分數階模型在時間軸0～4 s區間與實驗數據不能很好吻合的缺點，又能反映熱電偶整體溫度響應的變化特征。由于分數階算子可視為傳統算子微積分階數在相鄰整數值之間的插值，變階次分數階模型表達了分數階微分算子的階數插值性質。分數階微積分運算可以被視為冪函數和算子作用函數的卷積，因而更好地描述了熱電偶溫度分布特征的全局相關性，以及溫度分布的記憶和延遲性質。

5 結論

本文采用分數階微積分研究了熱電偶的動態特性。對于熱電偶測量固體表面瞬態溫度的問題，利用分數階建模和實驗建模相結合的方法，建立了一種熱電偶分數階傳遞函數的結構，給出了參數和階次的估計方法，在300～400 K溫度區間給出了一個鎳鉻- 鎳硅熱電偶的算例。得到如下結論：

1)分數階傳遞函數能夠表征熱電偶測量接點熱慣性延遲和熱電偶偶絲熱擴散單相延遲。

2)固定階次分數階模型中s0.5表征了熱電偶偶絲熱擴散引起的延遲只是延遲的一種弱化表示。

3)變階次分數階模型能夠通過階次的插值，用兩種分數階次組合表示測量接點熱慣性和熱電偶偶絲熱擴散所引起的延遲。