裝備保障任務分配建模與DLS-BCIWBA算法求解

王堅浩, 張 亮, 史 超, 車 飛, 張鵬濤

(空軍工程大學裝備管理與無人機工程學院, 陜西 西安 710051)

0 引 言

裝備精確保障的實質是指運用系統工程的理論和方法,通過精細、精確籌劃和運用裝備保障資源、保障力量,使其在準確的時間、地點完成裝備保障任務。裝備精確保障要求對各類裝備設施、器材、備件等資源和專業人員進行整合和編組,以保障單元的形式分配給具體的保障任務,屬于一類典型的任務分配問題[1]。求解此類任務分配問題,整數規劃、分支定界法和枚舉法等精確求解方法無法滿足實時性要求;而基于動態列表規劃的啟發式方法[2-4]求解效率較高,但都是采用基于貪心策略的局部搜索策略,因此得到的任務分配方案未必是最優方案;文獻[5-6]結合啟發式智能優化算法提出了混合任務分配方法,首先通過動態列表規劃 (dynamic list scheduling,DLS)選擇需要執行的任務,其次針對選定任務分配平臺(編組)問題的實質為多維0/1背包問題的特點,采用全局搜索遺傳算法(genetic algorithm,GA)和量子遺產算法(quantum genetic algorithm,QGA)相結合的混合啟發式智能優化算法,但并未考慮任務執行質量約束,然而在實際任務執行過程中,如果任務執行質量過低,則任務執行效果將遠低于期望效果;文獻[7]針對裝備保障任務分配問題,提出了基于優先排序和離散粒子群優化(particle swarm optimization,PSO)的混合任務分配方法。近年來,蝙蝠算法(bat algorithm,BA)[8]也應用于此類任務分配問題,且相比于GA和PSO具有更快的收斂速度和更好的全局尋優能力[9-10],但也存在算法后期收斂速度較慢、收斂精度不高、易陷入局部最優等問題。

本文首先建立了裝備精確保障協同任務分配問題的數學模型,設計了以DLS算法為主的求解框架,嵌套具有混沌搜索策略和入侵雜草算子的二進制混沌入侵雜草蝙蝠算法(binary chaotic invasive weed bat algorithm,BCIWBA)為選定任務分配保障單元。首先利用BA的全局尋優能力和迭代初期快速收斂性進行全局搜索;然后選取部分最優個體融合入侵雜草生長繁殖、空間擴散和競爭生存機制進行局部搜索,并通過學習因子和慣性權重的自適應協同更新以平衡探索和開發能力,結合脈沖頻率、響度、發生率變化區間的混沌搜索避免早熟收斂;最后通過案例仿真證明本文所提任務分配方法的有效性。

1 問題描述

1.1 基本概念

圖1 任務間的時序關系Fig.1 Sequential relationship of tasks

保障單元:擁有各類裝備設施、器材、備件等保障資源和專業人員的保障力量的編組,是保障任務的直接執行者。記包含M個單元的保障單元集為U={U1,U2,…,UM},對于?Uj∈U,其屬性包括:保障單元的初始地理坐標位置LUj=(XUj,YUj);保障單元平均移動速度VUj;保障單元具備的初始保障能力向量CUj={CUj1,CUj2,…,CUjL},CUjl為保障單元Uj第l項保障能力值,若CUjl=0,則表示保障單元Uj不具備第l項保障能力。

1.2 保障單元能力損耗及更新模型

保障過程中,保障單元執行任務會造成其保障能力的損耗,因此,在保障單元執行完某一任務后,應對其保障能力進行如下更新:

,l∈[1,L]

(1)

(2)

則更新后的保障單元能力值為

(3)

1.3 協同任務分配目標函數

當保障單元執行完成任務分配方案,其任務執行時間即為

(4)

裝備精確保障協同任務分配以最小化任務執行時間為目標,則目標函數為

(5)

1.4 協同任務分配約束分析

協同任務分配問題的約束條件包括:①任務-保障單元分配約束;②任務時序邏輯約束;③任務執行質量約束。

(1) 任務-保障單元分配約束

每一項任務成功執行至少需要分配一個保障單元,即滿足

(6)

(2) 任務時序邏輯約束

/VUj

(7)

若保障單元Uj在執行Ti之前執行的最后一項任務為Tj,則其到達任務Ti所在位置的時間為

/VUi+ETj

(8)

任務Ti的開始時間STi不小于先導任務Tk結束時間ETk和分配給其的所有保障單元的到達時間TITij之間的最大值,因此有

(9)

(3) 任務執行質量約束

保障單元執行任務Ti的質量定義為

(10)

式中,‖RTi‖為任務Ti能力需求類型的數量;CRil表示任務Ti的第l項能力需求滿足度,可以利用其獲得的保障能力CUjl與能力需求DTjl的比值表示,即

(11)

保障單元集執行所有任務的平均質量定義為

(12)

式中,Qavg∈[0,1],Qavg越大,保障單元集執行所有任務的質量越好。

保障單元集執行所有任務的平均質量Qavg必須高于某一下限閾值φ,否則將導致任務執行效果遠遠低于期望效果,即滿足

Qavg≥φ

(13)

1.5 協同任務分配數學模型

因此,以最小化TIT為目標,協同任務分配問題模型為

(14)

2 DLS-BCIWBA任務分配算法

2.1 算法流程

本文針對協同任務分配問題(14),提出了一種基于DLS和BCIWBA的協同任務分配算法,主要包含兩個環節,基于DLS的任務選擇和基于BCIWBA的保障單元分配,DLS-BCIWBA算法流程如圖2所示。

圖2 DLS-BCIWBA算法流程Fig.2 Flow chart of DLS-BCIWBA

2.2 基于DLS的任務選擇

其主要步驟如下:

步驟1定義過程變量:可執行任務集Tready、已執行任務集Tcomplete和空閑保障單元集Ufree;

步驟2初始化所有任務的優先權系數和保障單元能力向量;

步驟3更新Tcomplete任務執行時間,如果Tcomplete=?則跳過;

步驟4在前導任務已完成任務中,選擇優先權系數最大的一項任務;

步驟5為該任務在空閑保障單元集Ufree中選擇一項資源以滿足任務能力需求;

步驟6可執行任務集Tready和空閑保障單元集Ufree和保障單元能力更新;

步驟7判斷是否所有任務已完成分配,如果是則終止算法,否則轉入步驟2。

當任務Ti的所有直接前導任務都已執行完成,該任務Ti便進入可執行任務集Tready,在Tready中根據任務優先權系數依次分配保障單元,計算任務優先權系數的依據主要包括任務持續時間、直接后續任務數量及其優先權系數[6],任務優先權系數越大,表示任務優先級越高,任務優先權系數定義為

(15)

式中，PTi為任務Ti的優先權系數;OUT(i)為任務Ti的直接后續任務集。

2.3 基于BCIWBA的保障單元分配

2.3.1 基本二進制蝙蝠算法

BA的優化過程可以理解為蝙蝠群體從無序到有序的演化過程,在問題的解空間中,每個解都是一只蝙蝠,蝙蝠通過調整頻率、響度和脈沖發生率等參數,追隨當前適應度值最高的蝙蝠,直至尋找到全局最優解。因此,BA可視為標準PSO和由脈沖響度、脈沖發生率控制的集中局部搜索的一種均衡組合算法;此外,如果不更新蝙蝠速度,固定脈沖響度和脈沖發生率,BA又可以認為是一種簡化的和聲搜索(harmony search,HS)算法[11]。為了實現BA由連續域向二進制離散域的拓展,二進制蝙蝠算法(binary bat algorithm,BBA)應運而生[12],其算法流程如下。

步驟1初始化蝙蝠種群速度vi、位置xi和頻率fi、響度Ai和脈沖發生率ri(i=1,2,…,n)。

步驟2通過調整頻率產生新解(解即是蝙蝠位置),并更新速度和位置。

更新方式:

fi=fmin+(fmax-fmin)β

(16)

(17)

(18)

步驟3蝙蝠位置的二進制離散化操作。

BBA離散化操作實現標準BA由連續域向二進制離散域拓展,總結以往文獻中提出的離散化方式,除就近取整或四舍五入方式外,主要采用V型[12]、S型[13]和T型[14]邏輯函數映射實現離散化操作:

(20)

(21)

步驟4根據脈沖響度和發生率選擇局部最優解。

(22)

(23)

選擇局部最優解的偽代碼可表示如下:

end if

end if

步驟5排列所有蝙蝠適應度值,更新當前全局最優解。

步驟6根據迭代次數判斷終止準則。若滿足t>tmax,則算法終止,否則返回步驟2～步驟5。

2.3.2 BCIWBA算法

從當前空閑保障單元集Ufree中為選定的任務分配保障單元,其實質是多維0/1背包問題。基于多維0/1背包問題的特點和BBA算法流程,本文提出了一種BCIWBA算法,與標準BBA相比,BCIWBA主要在以下3個方面進行改進。

(1) 脈沖頻率、響度和發生率變化區間混沌搜索

BBA中脈沖頻率往往在頻率變化區間隨機取值,可能導致速度的變化陷入局部區間,甚至會被迫“停滯”[15];此外,根據脈沖響度和脈沖發生率選擇局部最優解的過程,當蝙蝠的脈沖發生率逐漸增大后,進行鄰域搜索的機會將越來越小,算法易陷入局部最優。

混沌是一種普遍的非線性現象,具有遍歷性、隨機性與確定性相統一的特點,為此,本文采用自適應折疊混沌搜索方法,通過混沌遍歷脈沖頻率、響度和發生率變化區間,使得蝙蝠脈沖頻率、響度和發生率得到充分變化,具體設計如下:

(24)

(25)

(26)

(27)

(2) 慣性權重和學習因子自適應協同更新

BBA雖然具有較強的全局搜索能力,但只是一味的向當前群體最優蝙蝠個體方向聚集,并按照式(17)和式(18)動態調整蝙蝠個體的飛行速度和位置,當所有蝙蝠個體聚集在當前最優個體附近,導致與最優個體差異較小時,蝙蝠個體的速度和位置更新越來越小,逐漸趨向同一化,從而使得蝙蝠種群個體多樣性大大降低,容易陷入局部最優。

因此,為了增加種群的多樣性,改變將所有蝙蝠均引導飛向當前最優蝙蝠個體的方式,本文將蝙蝠速度更新方式設計如下:

(28)

慣性權重選取非線性遞減慣性權重控制方案:

ωinital-ωfinal)

(29)

式中,k1∈Z+;ωinital和ωfinal為慣性權重初值和終值。

學習因子更新設計如下:

(30)

式中,k2∈Z+;ηinital為學習因子初值。

(3) 融合入侵雜草生長繁殖、空間擴散和競爭生存機制的局部搜索

BBA與大多數啟發式智能優化算法一樣存在后期收斂速度較慢、收斂精度不高、易陷入局部最優等問題,特別是針對高維任務分配問題,而入侵雜草優化(invasive weed optimization,IWO)算法[17]簡單,具有很強的局部搜索能力,因此在局部搜索過程中通過融合入侵雜草生長繁殖、空間擴散和競爭生存機制避免陷入局部最優。

IWO算法基于個體適應度即任務執行時間進行生長繁殖,選取適應度值排名前n/10個蝙蝠個體,各個蝙蝠的繁殖個數計算如下:

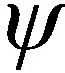
(31)

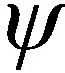
空間擴散階段蝙蝠個體在其父代附近以正態分布隨機擴散,正態分布標準差σ遞減變化過程如下:

(32)

式中,σinital和σfinal為標準差初值和終值;k3∈Z+為非線性調合指數。

IWO算法競爭生存機制是通過與預先設定的種群數量n比較來實現的,當迭代過程中種群數量大于n時,將種群中的父代和子代個體按照適應度值排序,適應度值排名前n個個體作為下一代種群。

3 仿真算例

以聯合作戰裝備精確保障想定為例,保障任務間時序邏輯約束關系如圖1所示,保障任務集為T={T1,T2,…,T18},保障單元集為U={U1,U2,…,U20},保障任務集平均執行質量下限閾值φ=0.8,保障單元各項保障能力的損耗系數ωl均設置為0.1,保障任務和保障單元屬性如表1和表2所示。

表1 保障任務屬性

表2 保障單元屬性

續表2

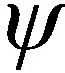
為了體現仿真算例實驗的有效性,通過對3種算法分別運行30次仿真計算實驗所得到目標函數值(任務執行時間TIT)的最優值、最差值、均值、標準方差和平均運行時間來考察算法性能,3種算法性能比較如表3所示。其中DLS-BCIWBA算法最優解對應的任務-保障單元分配方案如表4所示。

表3 3種算法優化性能比較

由仿真實驗結果可知,基于DLS-BCIWBA算法的協同任務分配方法具有較好的最優值、均值和方差,而且算法平均耗時稍短,因此相比于DLS-GA和DLS-QGA,基于DLS-BCIWBA算法的協同任務分配方案更為緊湊,時效性更優。

從統計學角度對3種算法優化性能進行比較,3種算法30次獨立運行實驗盒須圖如圖3所示。圖3中，盒代表指標的四分位差,盒越短,數據越集中;盒中的橫線代表數據的中位數,對于任務執行時間指標,中位數越小越好;盒上端的上須代表數據的最大值,盒下端的下須代表數據最小值,超出上下須的數據用“+”表示,代表該數據為異常值。由圖3可知,基于DLS-BCIWBA算法的協同任務分配方法在統計意義上能夠得到全局最優、穩定性最優和任務執行時間最為緊湊的任務分配方案。

表4 最優任務-保障單元分配方案

圖3 3種算法優化性能盒須圖Fig.3 Optimization performance boxplot of three algorithms

4 結 論

本文針對裝備精確保障協同任務分配問題,建立了以最小化任務執行時間為目標的數學模型,提出了一種DLS-BCIWBA混合任務分配方法,通過DLS選擇所需執行的任務,設計BCIWBA為選定任務分配保障單元。裝備精確保障協同任務分配案例仿真結果表明,基于DLS-BCIWBA算法的任務分配方法可以有效解決時序邏輯任務分配問題。