含有通信時滯的多航天器SO(3)姿態協同控制

董朝陽, 馬鳴宇,2, 王 青, 周 敏

(1. 北京航空航天大學航空科學與工程學院, 北京 100191; 2.北京電子工程總體研究所, 北京 100854; 3. 北京航空航天大學自動化科學與電氣工程學院, 北京 100191; 4. 北京仿真中心航天系統仿真重點實驗室, 北京 100854)

0 引 言

多航天器姿態協同是通過航天器之間的信息交互設計恰當的協同控制律,以使得各航天器姿態保持一致[1]。在航天器控制領域,姿態協同是很多應用的一個基本問題,具有重要的研究意義:多顆小衛星的協同工作需要對衛星間的相對姿態進行協調,以此可以完成復雜的任務,具有成本低、研制周期短、應用方式靈活等優點[2];同時,在航天器交會對接、衛星捕獲等航天作業中,姿態協同也是一項關鍵技術[3]。因此,多航天器系統姿態的協同控制的研究受到越來越多的關注[4-5]。協同控制一種分布式的控制方法,通?？梢苑譃椴捎谩爸?從”(leader-following)和無主(leaderless)結構的方法[6-8]。“主-從”結構的理論證明相對簡單,也取得了很多研究成果。但其方法需要利用主航天器的狀態,主航天器的失效會造成整個系統無法運行。無主結構的協同控制[9-10]不依賴某個特定航天器,降低了對拓撲結構的要求,更具有一般性,多航天器具體任務及應用可以在此方法基礎上發展得到。

多航天器系統模型由每個航天器的姿態描述和相互之間的拓撲組成。需要注意的是,在現有的大部分文獻中,對航天器姿態均采用俯仰/偏航/滾轉通道模型或四元數描述模型,存在一定的局限性:姿態方程在歐拉角360°大范圍變化時會存在奇異問題,導致基于這種模型設計的控制器也只適用于某個范圍內。四元數的姿態表示方法避免了奇異性,但四元數到旋轉矩陣的映射是雙重覆蓋的,不具有唯一性,用于控制時可能導致姿態散開,引起系統性能下降[11-12]。為了避免這些問題,相關文獻提出了基于特殊正交群SO(3)的姿態建模與控制方法[13-15]。采用SO(3)方法能夠從整體的角度對姿態進行描述,從而使模型得到簡化。同時,姿態與旋轉矩陣是一一對應的,相比傳統歐拉角區分通道設計的方法更為統一,且不存在姿態奇異問題,更適用于多航天器的協同控制。針對單個飛行器,文獻[16]研究了SO(3)上全局鎮定問題,并給出了其在姿態跟蹤控制中的應用。文獻[17]研究了面向無人機的SO(3)滑模變結構姿態控制器,實現了對無人機的大角度跟蹤。在多個體控制方面,文獻[18]提出了多剛體的姿態運動SO(3)協同控制,但要求通信拓撲是雙向的。

在實際的多航天器系統中,由于通信線路的負載、信息交互的不對稱性及傳輸速度的限制,航天器之間的通信拓撲是有向的。同時,通信時滯也很難避免,而時滯的出現會影響整體的協同性能,甚至造成系統的不穩定[19]。因此,在協同控制設計過程中,有必要考慮通信拓撲的有向性以及通信時滯的影響。對于時滯系統的控制問題,文獻[20]研究了無向拓撲下衛星編隊姿態協同跟蹤控制,采用一階濾波器來設計存在通信時滯的輸出反饋控制器;文獻[21]提出了魯棒濾波器來補償系統的輸入時滯,并在四旋翼無人機姿態控制中進行了應用,但是這種方法需要姿態小角度假設;文獻[22]研究了“主-從”拓撲形式下存在時滯的衛星姿態協同控制;文獻[23]基于反步法提出了航天器姿態時滯控制方法,在強連通拓撲的條件下使得系統是穩定的。

需要注意的是,在現有的文獻中采用SO(3)的姿態控制方法還比較少,且大多集中在個體飛行器,對于多飛行器SO(3)協同控制的研究還比較有限,同時沒有考慮存在時滯情況下的設計與穩定性分析問題。文獻[18]提出的方法不僅要求通信為雙向的,也很難直接應用于存在時滯的情形。為此,本文針對含有通信時滯的多航天器系統,在有向拓撲的環境下提出了基于SO(3)的姿態協同控制方法。由于SO(3)與傳統姿態描述不同,文中首先對SO(3)上的協同指令進行了研究,根據通信拓撲結構提出了旋轉矩陣形式的姿態指令。在此基礎上,利用SO(3)形式誤差設計標稱控制器,提出采用補償濾波器來處理系統中的時滯狀態,共同構造了協同控制器,證明了多航天器能夠實現姿態協同。文中使用包含5個航天器的控制系統對所提方法進行了仿真,仿真結果與理論分析相符,驗證了基于SO(3)協同控制方法的有效性。

1 多航天器姿態控制系統模型建立

1.1 航天器姿態運動SO(3)模型

在三維空間中,本體坐標系與慣性系之間的旋轉變換可以用一個正交變換矩陣R來表示,所有的正交變換矩陣構成了SO(3)群:

SO(3)={R∈R3×3|RRT=I3,detR=1}

(1)

任意姿態都對應一個矩陣R∈SO(3)。因此,航天器的姿態就可以用SO(3)中對應的元素R來表示。令Ω=[ω1ω2ω3]T,定義運算

(2)

為hat映射。hat映射的逆運算∨稱為vee映射,其將任意三維反對稱陣映射為三維向量,即

ω1ω2ω3]T

(3)

基于上述分析,建立航天器i的姿態運動方程為

(4)

1.2 航天器通信拓撲描述

2 基于SO(3)的姿態協同指令設計

(5)

(6)

(7)

在得到設計的姿態指令信號Rdi后,定義SO(3)中的相對姿態誤差和角速度誤差為

(8)

(9)

(10)

(11)

(12)

(13)

同時,根據SO(3)的性質可知,有如下關系成立:

(14)

(15)

3 多航天器協同控制器設計

3.1 SO(3)協同控制器

在完成姿態指令設計后,本節提出了基于SO(3)的航天器協同控制器以完成對指令的跟蹤,同時實現姿態一致。

根據式(9)和式(15),航天器i的誤差方程可以表示為

(16)

進而設計如下形式的姿態協同控制器:

Mi(t)=ui(t)+ufi(t)

(17)

(18)

式中

Ξi+Δi+ufi+ui=

-kRieRi-kΩ ieΩ i+Δi+ufi

(19)

(20)

于是,記Gi(s)=Fi(s)(I3-Fi(s))-1,最終得到補償控制器為

ufi=-Gi(s)(JiseΩ i+kRieRi+kΩ ieΩ i)

(21)

3.2 姿態協同穩定性分析

將補償濾波器Fi(s)表示成狀態空間形式可得

(22)

式中

k=1,2,3;b=[1 0]T;c=[1 0]T

Δi-kRiBReRi

(23)

式中

引理2[13]記函數

(24)

則Ψ(Ri,Rdi)的下界可表示為

(25)

下面給出關于協同穩定性的結論。

定理1考慮N個航天器組成的系統(4),其通信拓撲由L給出且通信存在時滯τi(i=1,2,…,N)。若拓撲包含生成樹,那么根據所設計的姿態協同指令式(10)～式(12)和控制器式(17),多航天器系統是穩定的且能夠實現姿態協同。

證明選取Lyapunov函數為

(26)

首先證明V1i的正定性。易知

(27)

(28)

記zi=[‖eRi‖‖eΩ i‖]T,結合引理2可知

(29)

(30)

V1i中的第3項的導數為

(31)

同時,由式(18)可知

(32)

(33)

式中,kδ、δi為某正常數。進一步通過式(17)、式(18)和式(33)可得

(34)

根據以上分析,V1i對時間t求導數可得

≤

(35)

將式(35)進行化簡,記

(36)

(37)

則有

≤-μ1‖eRi‖2-(k-κ3)‖xfi(t)‖2+

(38)

再選取Lyapunov函數V2i為

(39)

(40)

進而,對V2i求導數并進行化簡得到

(41)

式中

(42)

(43)

(44)

≤-μ1‖eRi‖2-μ2‖eΩ i‖2-(k-κ3)‖xfi(t)‖2-

(45)

(46)

(47)

(48)

(49)

證畢

注4通過航天器建模(4)和控制器(17)設計過程可以看出,提出的SO(3)協同控制方法允許各航天器的參數是不同的,即適用于航天器異構的情況。

4 多航天器協同控制仿真驗證

在本節中,考慮由5個航天器組成的系統,對所設計的協同控制方法進行仿真。各個航天器的參數和初始條件如表1所示。

表1 航天器參數和初始條件

初始姿態對應的R陣為

航天器之間的通信拓撲如圖1所示。對應的邊的權重為a14=1,a23=1,a32=0.3,a35=0.7,a41=0.5,a43=0.5,a51=1。通信時滯設置為0.1 s。由此可以通過式(10)～式(12)得到姿態協同指令。

圖1 航天器通信拓撲Fig.1 Communication topology between spacecraft

在姿態協同控制器中,選取kRi=5,kΩ i=12.5,Ffi=diag{10,10,10}。在協同控制系統設計與仿真的過程中均使用的是基于SO(3)的方法,采用選擇矩陣R對姿態進行描述。在圖2～圖4中為了便于結果呈現,將R轉換成俯仰、偏航、滾轉角度進行表示。由圖2～圖4可知,在各個航天器姿態初始值相差較大的情況下,仿真開始后能夠以較快的速度收斂到共同值,實現了姿態協同。

圖2 多航天器俯仰角變化曲線Fig.2 Illustration of the pitch angles of spacecrafts

圖3 多航天器偏航角變化曲線Fig.3 Illustration of the yaw angles of spacecrafts

圖4 多航天器滾轉角變化曲線Fig.4 Illustration of the roll angles of spacecrafts

為了具體描述協同誤差的收斂情況,在仿真中定義:

(50)

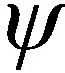
圖5 協同誤差和跟蹤誤差收斂曲線Fig.5 Illustration of the consensus and tracking errors

進一步為了說明控制輸入的變化,文中在圖6和圖7中以航天器4和航天器5為例,給出了其控制力矩曲線,其他航天器控制輸入與此相似。由仿真結果可知,提出的控制器保證了姿態協同和系統的穩定性,在時滯存在的情況下能夠滿足設計要求,基于SO(3)的姿態協同控制是有效的。

圖6 航天器4的控制輸入Fig.6 Control inputs of the 4th spacecraft

圖7 航天器5的控制輸入Fig.7 Control inputs of the 5th spacecraft

5 結 論

本文研究了多航天器系統的姿態協同問題,在考慮通信拓撲為有向圖且存在時滯的情形下,提出了基于SO(3)的協同控制方法。相比傳統俯仰、偏航和滾轉區分通道或四元數的表示形式,文中采用SO(3)中的旋轉矩陣建立了航天器姿態協同控制模型。進一步,利用相鄰航天器的狀態信息,給出了SO(3)相對姿態誤差的定義和協同指令設計方法。在此基礎上,采用濾波器對系統通信時滯進行了補償,設計了SO(3)協同控制器實現對指令的跟蹤,保證多航天系統姿態達到一致。提出的方法允許航天器是異構的,更符合實際的工程應用,而通過指定“主航天器”、加入特定跟蹤指令等方法,本文研究的協同控制方法也可以推廣到姿態指向協同和同步跟蹤地面點等具體應用情形。仿真結果驗證了提出的基于SO(3)的協同控制方法的有效性。