解三角形知識大闖關

■河南省洛陽市汝陽一高 張海濤

解三角形是初中解直角三角形問題的直接延伸,也是三角函數和平面向量知識考查的重要載體,同時也是解決三角形中計算問題及生產、生活實際問題的重要工具,具有重要的應用價值,屬于高考的必考內容。主要通過三組公式(正弦定理、余弦定理、面積公式),通過問題導學,激活知識構建的前后聯系。解決問題的基本方法主要是通過邊角互化,即“化角為邊(代數恒等變換),化邊為角(三角恒等變換)”來實現優化解題,要求對公式、定理靈活運用,能夠逆用、變形使用等,通過余弦定理建立三邊關系,通過正弦定理建立邊角關系,轉化為三角函數問題或者借助三角形的某一頂點的軌跡,借助圖形,如外接圓來解決。從角的思路解題較為煩瑣,但是具有通用性;從形的角度解題,通過臨界位置,可以求解最值;從三角、三邊之外的非基本元素,如高、中線、角平分線等入手,比較靈活,結合方程思想、化歸思想可以解決三角形有關的動態問題,如有關角、邊、面積、周長的范圍問題。總之,解三角形問題近年來試題內容豐富多彩,集知識的交匯性、綜合性于一體,極富挑戰性,值得我們重視。

下面,我們依據題目的特點把解三角形問題大致歸納為如下幾個類型,便于讓同學們做一題而知一類,觸類旁通,提高學習效率。

第一關：邊、角、周長、面積具體求值問題

(一)求邊。

試題點評：解法1是運用正弦定理“邊化角”,而使用正弦定理的一個基本條件是“齊次”,因此,結合條件a2-c2=2b得到b=就是非常自然的事情,然后再使用正弦定理并結合條件求出b;解法2則是運用余弦定理“角化邊”,結合題目所求“直奔主題”。本題還有很多求解方法,讀者可以自行嘗試。

(二)求角。

例2 已知在△ABC中角A,B,C的對邊分別為a,b,c,且2（a2-b2）=2accosB+bc,則A=。

解法1(化角為邊)：由余弦定理得a2+c2-b2=2accosB。

代入已知條件,得:2（a2-b2）=a2+c2-b2+bc,故a2-b2-c2=bc。

解法2(化 邊 為 角)：由2（a2-b2）=2accosB+bc及正弦定理可得:

2sinAsinCcosB+sinBsin C=2(sin2A-sin2C)=2sin(A+B)sin(A-B)=2sinCsin(A-B)。

因為sinC＞0,故2sinAcosB+sinB=2sin(A-B),sin B=-2sinBcosA,所以cosA=-,A=。

試題點評：解法1是觀察所求與條件發現可利用余弦定理消除角,得到邊的關系,再次利用余弦定理恰好求得角A;解法2則根據所給條件兩邊為齊次結構,恰好可以利用正弦定理邊化角,對恒等式左側利用兩角正弦的平方差公式sin2A-sin2B=sin(A+B)·sin(A-B)實現降次,結合和差公式逆用求得角A。

(三)求周長。

例3 在△ABC中,角A,B,C所對的邊分別為a,b,c,若b=5,C=60°,且△ABC的面積為5,則△ABC的周長為。

所以△ABC的周長為9+21。

試題點評：要求周長需先求a,c,觀察所給邊角及面積三個條件發現恰好可以求解a,進而根據知三求二利用余弦定理得到邊c,從而完成周長求解。

(四)求面積。

例4 在△ABC中,角A,B,C所對的邊分別為a,b,c,若A=,a=4,角A的平分線交邊BC于點D,其中AD=3,則△ABC的面積S△ABC=。

在△ABC中根據余弦定理可得:b2+c2-bc=112。②

聯立①②可得bc=48。故S△ABC=bcsinA =12。

試題點評：題目給出了含有邊的三個條件,但這三個條件是“分散”的,要想求出面積,如何將條件AD=33轉化成“有用”的條件是解題的關鍵。解法1是設法求出∠ADC的正弦值,再根據△ABC是△ABD和△ADC之和,應用正弦定理求解;解法2則是根據S=bcsin A,綜合利用題目△ABC所給條件求出bc,從而求出面積。

第二關：求解邊、角、周長、面積的范圍與最值及判斷三角形形狀問題

(一)求邊的范圍與最值問題。

例5 已知△ABC的內角A,B,C的對邊分別為a,b,c,且（a2+b2-c2）（acosB+bcosA）=abc,若a+b=2,則c的取值范圍為( )。

試題點評：觀察所給條件中的結構acosB+bcosA,根據射影定理得到其恰好為c,進而實現角化邊,自然想到利用余弦定理求解角C,再次利用余弦定理得c2=4-3ab,觀察條件a+b=2想到利用基本不等式求解最大值,結合三角形三邊關系求得周長范圍。

(二)求角的范圍與最值問題。

例6 在△ABC中,若tanA,tanB,tanC依次成等比數列,則∠B的取值范圍為。

解法1(余弦定理+基本不等式)：sinCcos2B。

解法2(正弦定理+余弦定理)：

由tan2B=tanAtanC及正弦定理得:

試題點評：解法1中,初看題目自然想到要進行切角化弦,得到sin2BcosAcosC=sinAsinCcos2B,兩邊角的名稱恰好互余,只能用正弦、余弦定理繼續化簡,發現b2=,確實復雜,繼續進行,再看目標是求角B的范圍,利用余弦定理將cosB轉化為a,c的齊次式,柳暗花明,利用基本不等式恰好得到其范圍,進而求得角B的范圍。

(三)求周長的范圍與最值問題。

例7 在銳角△ABC中,角A,B,C所對的邊分別為a,b,c,且c=1,A=2C,則△ABC的周長的取值范圍為。

(四)求面積的范圍與最值問題。

例8 在△ABC中,a,b,c為角A,B,C的對邊,若a2+b2+2c2=8,則面積的最大值為。

解法3：由題意和余弦定理得8=a2+b2+2(a2+b2-2abcosC)=3(a2+b2)-4abcosC≥2ab(3-2cosC)。

試題點評：本題難度較大,僅僅給出邊的關系,要求面積的最大值,結合面積公式包含的元素——兩邊及其夾角的正弦,自然想到通過通過兩個定理轉化為邊或角的函數,利用不等式性質求解其最大值,或者轉化為角的關系,利用定點與單位圓上點的連線的斜率的范圍求解。

(五)三角形形狀的判定問題。

A.銳角三角形 B.直角三角形

C.鈍角三角形 D.無法確定

由圖2中A可知，添加酶的試驗組中，辣椒堿、辣椒二氫堿和辣椒紅色素的含量均較空白組高。且由圖2中B可知，3種物質的含量隨酶添加量的增大而增大，在酶添加量為0.3%(W/W)時，辣椒堿、辣椒二氫堿的含量達到最大值。在酶添加量為0.2%(W/W)時，辣椒紅色素的含量達到最大。分析原因可能是，當酶添加量較低時，底物過量，酶解不完全，致使辣椒中的有效成分溶出率不高，隨著酶添加量的增加，酶解作用增加，辣椒中關鍵物質的溶出率也隨著增加，而當酶添加過量時，由于酶與底物的結合飽和，3種物質的含量不會繼續增長。

試題點評：判斷三角形的形狀應圍繞三角形的邊角關系進行思考,可用正、余弦定理將已知條件轉化為邊邊關系,通過因式分解、配方等方式得出邊的相應關系,從而判斷三角形的形狀,也可利用正、余弦定理將已知條件轉化為角與角之間的關系,通過三角變換,得出三角形各內角之間的關系,從而判斷三角形形狀。

第三關：多知識點融合問題

(一)求參數問題。

例10 在△ABC中,角A,B,C的對邊分別為a,b,c,已知sinA+sinB+λsinAsinB=0,且a+b=2c,則實數λ的取值范圍是。

解：由a+b=2c結合正弦定理可得sinA+sinB=2sinC。

(二)與向量結合的問題。

例11 若G為△ABC的重心,且AG⊥BG,則sinC的最大值為。

解法1(向量夾角+基本不等式)：

試題點評：解法1通過賦值,結合三角形法則及直角三角形斜邊中線性質及重心性質巧妙構造方程組,得到根據整體性把握,立刻會想到利用基本不等式去解決;解法2的解題思路殊途同歸,重在利用據數量積為0轉化得到結論再利用不等式解決。

(三)求比值問題。

解法2(余弦定理+余弦函數有界性)：

第四關：解三角形的實際應用問題

(一)求解高度問題。

圖1

例13 如圖1,飛機的航線和山頂在同一個鉛垂平面內,已知飛機所在處的海拔為20210m,速度為270m/s,飛行員先看到山頂的俯角為15°,經過100s后又看到山頂的俯角為30°,則山頂的海拔為。

圖2

答案：6710m

解析：如圖2。

AB=270×100=27

000

(m),在等腰三角形ABC中,BC=AB=27

000

試題點評：求解高度問題應注意:(1)在測量高度時,要理解仰角、俯角的概念,仰角和俯角都是在同一鉛垂面內,視線與水平線的夾角;(2)準確理解題意,分清已知條件與所求,畫出示意圖;(3)運用正、余弦定理,有序地解相關的三角形,逐步求得問題的答案,注意方程思想的運用。

(二)測量距離問題。

圖3

例14 如圖3所示,從氣球A測得正前方的河流的兩岸B,C的俯角分別為75°,30°,此時氣球的高度是60

m,則河流的寬度BC等于( )。

答案：C

圖4

試題點評：求解距離問題應注意:(1)選定或確定要求解的三角形,即所求量所在的三角形,若其他量已知則直接解;若有未知量,則把未知量放在另一確定三角形中求解。(2)確定用正弦定理還是余弦定理,如果都可用,就選擇更便于計算的定理。

(三)解決測量角度問題。

例15 甲船在A處觀察到乙船在它北偏東60°的方向,兩船相距akm,乙船正在向北行駛,若甲船的速度是乙船的3倍,則甲船應取北偏東θ方向前進,才能盡快追上乙船,此時θ=。

圖5

答案：30°

解析：如圖5所示,∠CAB=60°-θ,∠B=120°,設追上乙船的時間為x,則BC=x,AC=x,在△ABC中,根據正弦定理得即,解得sin(60°-θ)=,又60°-θ為銳角,所以60°-θ=30°,θ=30°。

試題點評：求解測量角度問題應注意:(1)明確方位角的含義;(2)分析題意,分清已知與所求,再根據題意正確畫出示意圖,這是最關鍵、最重要的一步;(3)將實際問題轉化為可用數學方法解決的問題后,注意正、余弦定理的“聯袂”使用。

第五關：能力提升專訓

2.如果不等式ksin2B+sinAsin C＞19sinBsinC對任意△ABC都成立,則實數k的最小值為。

解(正弦定理+三邊關系)：

解：設a,b,c分別為角A,B,C的所對的邊,由題意得b=c+1,a＞2。

所以△ABC的周長為:

4.在△ABC中,內角A,B,C的對邊分別為a,b,c,且BC邊上的高為取得最大值時,內角A的值為。

圖6

圖7

解：先考慮一般情況,如圖8所示。

設∠PAC=α,∠PAB=β,PA=a,其中α,β為常數,∠APC=x(x為變量)。

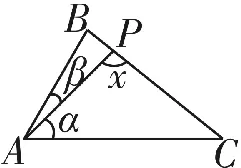
圖8

圖9

解法2(引入變量構造方程組)：如圖9,取D,E兩點,使AD=BD,作DE⊥AC于點E,設DE=3t,則CD=5t,CE=4t,AE=66t,AD=BD=15t。

解法3(利用正弦定理及積化和差公式)：

10.在△ABC中,ccosB+3bcosC=0,則角A的最大值為。

11.△ABC中,A,B,C成等差數列,a2+c2=kb2,則實數k的取值范圍是。

A.直角三角形

B.等腰三角形

C.等邊三角形

D.等腰或直角三角形

圖10

解法2：如圖11所示,AE為△ABC外接圓的直徑。

(1)D與O不重合,則AE⊥BC,△ABC為等腰三角形;

圖11

圖12

A.2.2 B.2

C.1.8 D.1.6