等差數列的一個性質及其應用
2018-09-28 05:54:38陜西省武功縣教育局教研室特級教師
中學生數理化(高中版.高二數學) 2018年9期
■陜西省武功縣教育局教研室 李 歆(特級教師)
同學們知道在等差數列學習中,有一個重要的性質:
已知{an}是等差數列,若m+n=p+q,則有am+an=ap+aq。
這個性質反映了等差數列第m項am、第n項an、第p項ap、第q項aq之間的等量關系,由此可以聯想,等差數列{an}前m項的和Sm、前n項的和Sn、前p項的和Sp、前q項的和Sq之間,是否也存在著某種等量關系呢?經過探究,得到如下一個性質:
性質:設Sm,Sn,Sp,Sq分別為等差數列{an}的前m項的和,前n項的和,前p項的和,前q項的和,且m+n=p+q,則有(p≠q)。
證明:設等差數列{an}的首項為a1,公差為d,則由等差數列的前n項和公式,可得
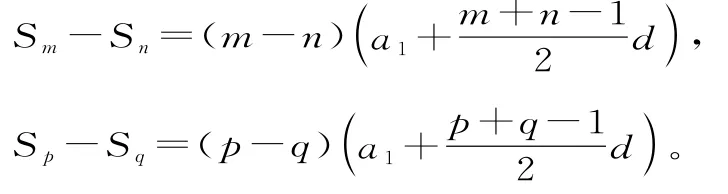
整理以上兩式,即得結論。
用上述結論解題,關鍵在于合理地選擇下標m,n,p,q。
例1 已知{an}為等差數列,a1=1,S5-S2=6,則S6=( )。
A.9 B.10 C.11 D.12

點評:由于a1=S1,且S1,S2,S5,S6的下標之間滿足關系:1+6=2+5,所以可以用性質求解。
例2 已知{an}為等差數列,a3+a4=8,則S5-S1=( )。
A.8 B.16 C.24 D.32
點評:從已知條件中求不出a1和d的值,只能得到a1和d的某個關系式,最后還需要將S5-S1轉化為含有這個關系,比較麻煩,但將已知條件a3+a4=8,轉化為S4-S2=8,用性質求解卻極為簡便。

點評:已知條件和所求問題中,出現了S2,S3,S4,S5,下標之間滿足關系式:2+5=3+4,可用性質解題。

點評:在此解法中,先引入了一個中間量S3,最后又聯立方程消去S3,既體現了“設而不求”的解題方法,同時又滲透了“方程思想”。
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
中等數學(2020年6期)2020-09-21 09:32:38
中等數學(2019年6期)2019-08-30 03:41:46
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02

