淺談三角形中的最值問題及解法
■重慶市鐵路中學校 何成寶
解三角形中的最值問題,在近幾年各類考試中頻繁出現,頗受命題者的青睞。這類問題的實質是將幾何問題轉化為代數問題,主要運用三角形的內角和定理、正余弦定理、面積公式、三角恒等變形、三角函數的性質,以及基本不等式等知識解題。下面舉例說明三角形中最值問題的類型及解法,供同學們參考。
一、已知角的等量關系
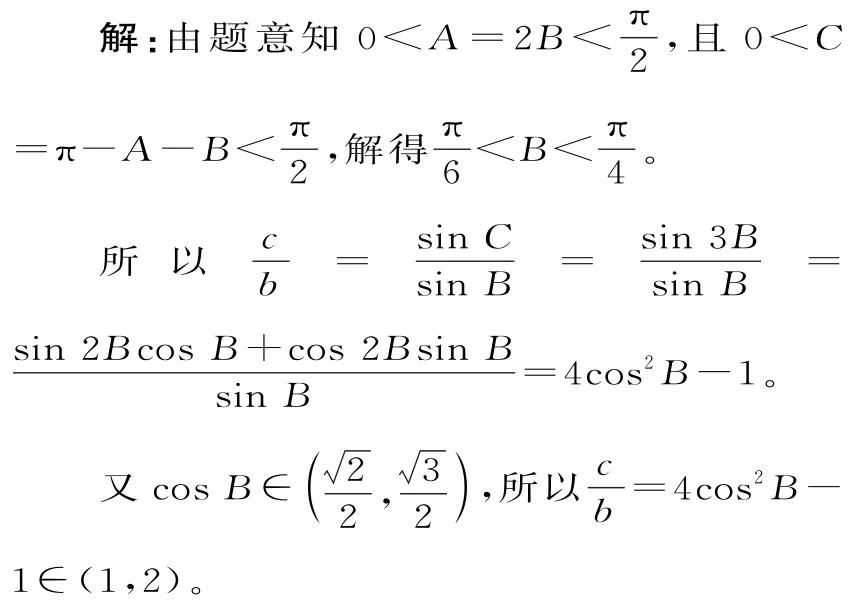
點評:①本題容易忽視“△ABC是銳角三角形”這個條件。②本題涉及三角形邊角之間的關系,考查邊角互化知識,化多元為一元,體現了解題的通性通法。
練習:在銳角△ABC中,A=2B,AC=1,則BC的取值范圍是。

二、已知一邊和該邊的對角
例2 在△ABC中,角A,B,C的對邊分別為a,b,c,且b=5,B=,求△ABC的周長的取值范圍。

點評:對三角函數式的處理常常借助于同角三角函數間的關系、誘導公式以及恒等變換式等實施變形,達到化簡、求值的目的。
練習:在△ABC中A,B,C所對的邊分別為a,b,c,且a=,A=,求△ABC的面積的最大值。

三、已知三邊的等量關系
例3 在△ABC中,a2+b2=c2+ab,若△ABC的外接圓半徑為△ABC的面積的最大值為。
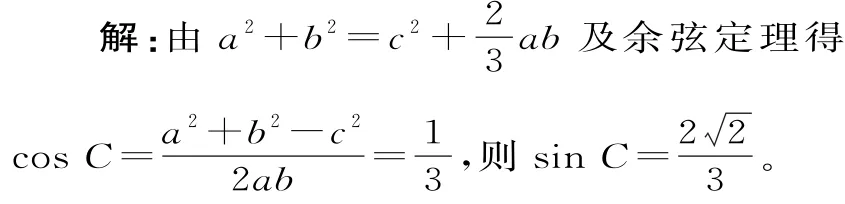
又由于c=2RsinC=4,所以c2=a2+b2-2abcosC ,16+,即ab≤12。
點評:先利用余弦定理求cosC的大小,再求出sinC的大小,然后利用三角形的面積公式結合基本不等式,求三角形面積的最大值。
練習:若△ABC的三邊a,b,c成等比數列,a,b,c所對的角依次為A,B,C,則sinB+cosB的取值范圍是。
解:由題設知b2=ac。

點評:本題將數列、基本不等式、三角函數、解三角形等知識結合起來,有利于提高同學們的綜合解題能力。
四、已知一邊和另兩邊的等量關系


點評:本題結合函數的知識,以同學們熟悉的三角形為載體,考查了三角形的面積公式、余弦定理等知識,是一道考查解三角形的好題。
練習:已知△ABC中,AB=2,AC=3BC,則△ABC面積的最大值是。解:設BC=x,則AC=3x。根據面積公式得:

五、已知向量的等量關系



