基于SPSS的西藏大學高等數學成績的方差分析

舒博爾 王思雪

【摘 要】對西藏大學理學院2017級非數學專業和工學院2017級信息工程專業2017——2018第二學期大學數學公共課“高等數學”的成績進行了方差分析，觀察不同性別、不同學院大學數學公共課的成績差異情況，發現其中存在的問題并提出有針對性的建議。

【關鍵詞】SPSS；西藏大學；高等數學成績；方差分析

在高等教育中，高等數學課程是非常重要的一門基礎課，也是西藏大學非常重視的一門大學數學公共課程。然而，高等數學的教學質量問題似乎并沒有因為它的重要性和校方的重視而提高。近年來，學生對該門課程的態度是敬而遠之，這也說明了學校和教師為提高高等數學教學質量所做的努力，并沒有達到預期的目的。那么，如何提高高等數學的教學質量呢？對此問題，國內外的學者和教育專家從影響高等數學教學質量的因素入手，通過調查問卷和統計分析的方法確定了學生主動性和教師業務能力這兩方面的原因，并給出了改進策略。但是這些研究成果都是針對高職高專和教學型本科院校，不適合教學研究型大學的實際狀況。鑒于此，本文以西藏大學理學院2017級非數學專業和工學院2017級信息工程專業2017——2018學年第二學期期末成績為樣本，從性別與專業這兩個因素進行方差分析，檢驗其對高數成績的影響顯著性，為新的管理體制與制度的制定奠定定量化的理論支撐。

一、成績的描述性分析

所用的分析軟件為SPSS21.0，首先將數據錄入到SPSS21.0軟件中，如果將成績作為觀察值，那么性別和專業是兩個因素。性別這一因素分為兩個水平，一個是男，記為1，一個是女，記為2。專業這一因素分為兩個水平，一個是理學院2017級非數學專業，記為1，一個是工學院2017級信息工程專業，記為2，則將2017級兩個學院不同專業190名學生的信息輸入到SPSS21.0中。

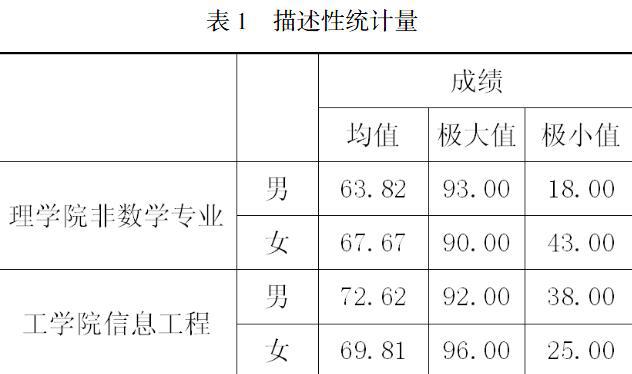
將數據輸入到SPSS21.0中之后，首先進行對成績進行描述性統計分析，利用分析——一般線性模型——單變量命令，得到各描述性統計量，如表1。

根據表1，得知理學院非數學專業學生男生成績最高為93，最低為18，平均分為63.82，女生成績最高為90，最低為43，平均分為67.67；工學院信息工程男生成績最高為92，最低為38，平均分為72.62，女生成績最高為96，最低為25，平均分為69.81。可以看出，對于理學院非數學專業，男生的最高分比女生高，而最低分比女生低，平均分也比女生低；對于工學院信息工程專業，男生的最高分比女生低，而最低分比女生高，平均分也比女生高；而就兩個學院不同專業來看，工學院信息工程專業學生高等數學成績最高分為96，比理學院非數學專業學生最高分93高出3分，而最低分為25卻比理學院非數學專業學生最低分18高7分，且工學院信息工程專業學生高等數學平均成績也明顯比理學院非數學專業學生高。那么不同專業、不同性別對成績的影響是否達到顯著程度呢？性別與專業兩個因素對成績這一觀察值有沒有交互影響呢？下面就通過方差分析的方法進行分析。

二、成績的兩因素方差分析

方差分析的目的在于了解性別和專業兩個因素對成績這一因變量取值是否有顯著性影響，文中因涉及兩個因素，所以使用兩因素方差分析方法。

（一）方差齊性檢驗

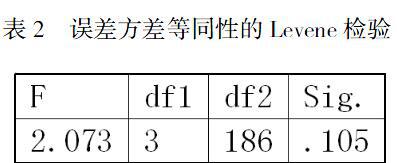
方差分析有個重要前提，那就是每組因變量的總體服從正態分布，且每組總體方差相等，因此先進行SPSS21.0的Levene檢驗，檢驗結果如表2所示。

從表2得知，對各組進行Levene檢驗后得到的P值為0.105，大于0.05的顯著水平，所以我們認為原假設成立，即各組的總體方差相等，即方差齊性，所以可以對成績進行兩因素方差分析。

（二）對成績進行兩因素方差分析

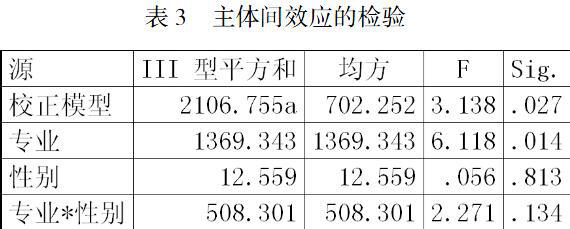
在SPSS21.0中對成績進行兩因素方差分析，首先分析主體間效應的檢驗，通過SPSS21.0軟件得到表3所示。

表3中顯示，該檢驗的顯著性等于0.027，小于0.05，因此所用的兩因素方差分析模型有統計學意義，上面提到的專業，性別和交互作用中至少有一個是對成績有影響。專業一欄的p值為0.014，說明專業這一因素對成績影響顯著。性別一欄對應p值為0.813，說明性別這一因素對成績有影響，但不顯著。專業*性別一欄的P值為0.134，大于0.05的顯著水平，所以專業與性別對成績無顯著的交互影響。

三、結論分析

對成績進行了兩因素方差分析，成績為因變量，專業和性別為自變量，結果顯示，專業對成績有顯著影響，工學院信息工程學生的高等數學成績（71.22）明顯要高于理學院非數學專業學生（65.75），差距為5.47分；性別因素也在某種程序上對成績有影響，男生的高等數學平均成績為68.22分，女生的高等數學平均成績為68.74，差距為0.52分。而與專業對性別無顯著交互影響。

【參考文獻】

[1]呂士寶.雙因素方差分析在數學成績分析中的應用[J].學周刊，2018（18）：79-80.

[2]柴偉文，曹黎俠，馬玉彥.基于數字特征的高等數學考試成績的方差分析模型[J].教育現代化，2018，5（14）：190-193+245.

[3]郭萍.單因素方差分析在數理統計中的應用[J].長春大學學報，2014，24（10）：1370-1373.