基于“古典概率”的發展背景,培養學生創新思維能力
廣州工商學院基礎教學部 李 萍
法國數學家龐加萊曾說:“如果我們想要預見數學的未來,那么適當的途徑是研究這門學科的歷史和現狀。”概率論產生于17世紀中葉,是研究偶然、隨機現象的規律的數學理論。早期的概率論是一種經驗的科學,作為一門經驗科學的古典概率論最直接地起源于一種相當獨特的人類行為思想的探索:人們對于“機會的游戲”(英語中的“game of chance”)的研究思考。所謂機會的游戲,是靠運氣取勝的一些游戲,如賭博、抽獎、彩票等等。
為了更清楚地了解古典概率的發展脈絡,介紹發展歷史上的一些重要事件,其中,1774年,拉普拉斯在“論概率”一文中給出了概率的定義:概率指的是合適情況的個數占所有可能發生的情況的個數的比例。1820年(第三版)出版的著作《分析概率論》,是古典概率論的金字塔,給出了概率的古典定義:若一實驗的可能結果為n個具有相等可能性的事件,而且其中m個是有利于事件A的發生,則事件A發生的概率P(A)是:

隨著實驗次數的增加,一個事件出現的頻率總在一個固定數的附近擺動,顯示出一定的穩定性。R.von米澤斯把這個固定的數定義為該事件的概率,這就是概率的頻率定義。
古典概率的定義并不是很難理解,并且古典概率的公式在實際應用時也是比較容易的,但是在實際教學中,多數教師是直接給出古典概率的定義、公式,大部分還停留在填鴨式教學模式上,導致學生對古典概率的本質理解不透徹,不知道哪一種隨機事件是古典概型,從而不知道何時使用古典概率的公式,這些都不利于激發學生的創新思維能力。
下面通過對實際生活中的一道古典概率題的幾種解法的討論來說明如何在求解古典概率的過程中,激發學生的創新意識,培養學生的創新思維能力。
例:10件產品中有4件次品,從中任取2件產品,已知其中有一件是次品,求另一件也是次品的概率。(對于這道題,會有多種不同解法,整理出以下幾種)
解法1:設A={另一件也是次品},因為10件產品中有4件次品,從中任取2件產品,顯然取到哪兩件產品都是等可能的,所以樣本空間中樣本點總數為,而另一件也是次品的基本事件總數為由古典概型概率的計算公式,得
解法2:設A1={已知其中一件產品為次品},A2={另一件產品為次品},
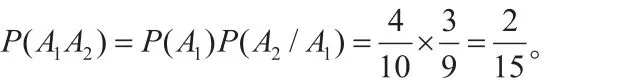
解法5:設A= {另一件產品也是次品}, 10件產品中有4件次品,從中任取2件產品,已知其中有一件是次品的樣本空間樣本點總數為,另一件也是次品的基本事件總數為,由古典概型概率的計算公式,得
上述答案中只有第4、5種解法是正確的,前三種解法都是錯誤的,那么為什么會出現這么多種錯誤的解法呢?原因還在于對題意不能正確地理解。
解法1的錯誤是把10件產品中有4件次品,從中任取2件,按常規計算得樣本空間總數為而沒有把題設條件“已知其中有一件是次品”考慮進去,從而把樣本空間中樣本點總數給擴大了。
解法2的錯誤是把題目中“已知其中有一件是次品”理解為抽取的第一件產品是次品,而把求“另一件產品也是次品”理解為在第一件產品是次品的條件下求第二件產品也是次品的概率。當然,這個題目用條件概率也是可以做的。
解法3的錯誤是把“已知其中有一件是次品,求另一件也是次品的概率”理解為抽取到的兩件產品都是次品的概率問題。
作為數學教師,在日常課堂教學中要經常地選擇一些發散性強的典型數學知識或問題,讓學生了解問題背景、知識背景,通過創設問題情境,形成創造氣氛,然后再通過問題解決,培養學生的創新思維能力。

