一類亞循環群同態個數的計算

張 良, 海進科

(1. 伊犁師范學院 數學與統計分院, 新疆 伊寧 835000； 2. 青島大學 數學與統計學院, 山東 青島 266071)

1 引言與預備知識

群的同態個數是群理論中的一個基本數量關系, 可以刻畫群的某些性質和結構, 目前已有許多研究結果. 例如: Frobenius[1]給出了n階循環群Cn到有限群G的同態個數滿足

Hom(Cn,G)≡0(mod(n,|G|)),

其中(n,|G|)表示n和|G|的最大公因數; Yoshida[2]推廣了文獻[1]的結果, 將循環群換成了有限交換群； Asai和Yoshida[3]猜想對任意有限群A和G, 均有Hom(A,G)≡0(mod(|A/A′|,|G|), 其中A′是A的換位子群, 并證明了在某些特殊情形該猜想成立. 文獻[4-5]計算了一些有限群到一般線性群的同態個數; 文獻[6]計算了一些有限群到一些經典群的同態個數; 文獻[6-11]分別計算了二面體群、 四元數群和模群等有限群之間的同態個數. 但對于一般亞循環群之間同態個數的研究目前尚未見相關文獻. 設n是正整數, 如果

(1)

則稱群Gn為4n階的亞循環群. 由文獻[12]知, 該類亞循環群存在. 本文計算該類亞循環群之間的同態個數, 并驗證該類亞循環群滿足Asai和Yoshida猜想. 本文考慮的群均為有限群,m,n≥2是正整數, 記Hom(Gm,Gn)是Gm到Gn的所有群同態構成的集合, |Hom(Gm,Gn)|是Gm到Gn的所有群同態個數； 記d=(m,n),m=m′d,n=n′d, 其中(m,n)是m,n的最大公因數,m′,n′是正整數. [m,n]表示m,n的最小公倍數. 其他記號參見文獻[12-13].

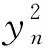
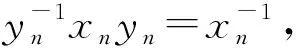
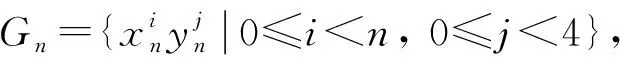
證明: 由群同態的定義及引理3可知結論顯然成立.

引理4設m,n≥2是正整數, 記d=(m,n),m=m′d,n=n′d, 其中(m,n)是m,n的最大公因數. 則(m′,n′)=1.

證明: 由最大公因數的性質可知結論成立.

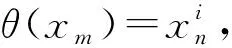
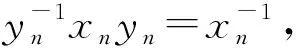
2 主要結果

定理1設m,n≥2是兩個奇數, 則|Hom(Gm,Gn)|=2+2n(m,n).

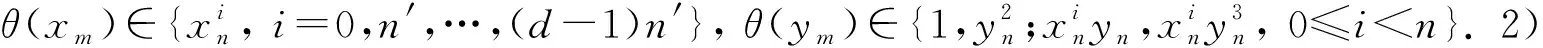
定理2設m>1是奇數,n是偶數, 則:

1) 當n≡2(mod 4)時, |Hom(Gm,Gn)|=8+2n(m,n);

2) 當n≡0(mod 4)時, |Hom(Gm,Gn)|=16+2n(m,n).

證明: 1) 當m是奇數且n≡2(mod 4)時, 分3步證明.

2) 當m是奇數且n≡0(mod 4)時, 分3步證明.

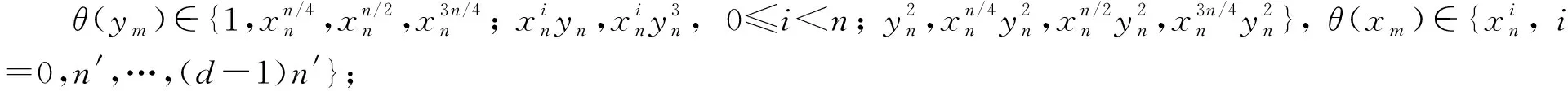
綜上可知定理2成立.

定理3設m是偶數,n≥1是奇數, 則|Hom(Gm,Gn)|=4+4n(m,n).

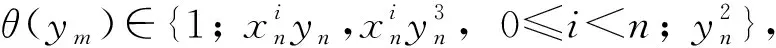
定理4設m,n是兩個偶數, 則:

1) 當n≡2(mod 4)時, |Hom(Gm,Gn)|=16+4n(m,n)；

2) 當n≡0(mod 4) 時, |Hom(Gm,Gn)|=32+4n(m,n).

證明: 1) 當m為偶數且n≡2(mod 4)時, 分5步證明.

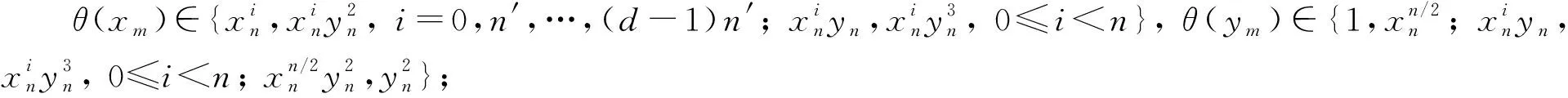
2) 當m是偶數且n≡0(mod 4)時, 分7步證明.

綜上可知, 定理4成立.

由定理1和定理4直接可得該類亞循環群的自同態個數滿足下列結論.

推論1設m≥2是正整數, 則:

1) 當m是奇數時, |End(Gm)|=2+2m2；

2) 當m≡2(mod 4)時, |End(Gm)|=16+4m2；

3) 當m≡0(mod 4)時, |End(Gm)|=32+4m2.

最后驗證該類亞循環群滿足Asai和Yoshida猜想.

推論2設m,n是兩個正整數,Gm,Gn分別為4m,4n階亞循環群, 則