L-Flou集范疇及其層表示

周 鑫, 劉 靜, 湯建鋼

(1. 伊犁師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 新疆 伊寧 835000; 2. 東北師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 長(zhǎng)春 130024;3. 伊犁職業(yè)技術(shù)學(xué)院 基礎(chǔ)部, 新疆 伊寧 835000)

模糊集[1]用于刻畫客觀事物的不確定性. 設(shè)X是一個(gè)非空集合, 集合X的模糊子集可由隸屬函數(shù)A:X→[0,1]刻畫, 其中:X稱為A的承載集, 記為K(A)=X; [0,1]稱為真值集. 為了使模糊集能刻畫更一般的事物, Goguen[2]引入了L-fuzzy子集的概念, 其真值集由比[0,1]更一般的完全分配格L代替.

由模糊集合的分解定理知, 一個(gè)模糊集對(duì)應(yīng)一族集合. 反之, 由模糊集的表現(xiàn)定理知, 一族集合可形成一個(gè)模糊集. Gentilhomme[3]定義了一種刻畫模糊集的非經(jīng)典集合——flou集的概念; 文獻(xiàn)[4]給出了L-flou集的概念及性質(zhì), 并得到了L-fuzzy集與L-flou集的格同構(gòu)關(guān)系. 文獻(xiàn)[5]研究表明,L-flou集可用集合套表現(xiàn), 使其表示模糊信息時(shí)既增強(qiáng)了模糊信息的表達(dá)精度, 又避免了單點(diǎn)隸屬度確定困難的問題. 基于此,L-flou集理論在處理信息等領(lǐng)域應(yīng)用廣泛.

本文利用范疇理論, 將真值集L視為范疇L, 給定元素的隸屬度視為范疇中的對(duì)象, 用態(tài)射刻畫不同隸屬度之間的關(guān)系, 給出L-fuzzy集范疇Set(L )與L-flou集合范疇Set(fL )的同構(gòu)關(guān)系, 并結(jié)合文獻(xiàn)[6-7], 得到了范疇Set(fL )同構(gòu)于賦予層結(jié)構(gòu)的集合范疇SetL(S H ).

1 預(yù)備知識(shí)

定義1[2]設(shè)X∈Ob(Set), 函數(shù)A: X→L稱為集合X的L-fuzzy子集, 也稱為L(zhǎng)-子集或L-集, 記做(X,A). 在承載集合X確定且不至引起混淆的情況下, 簡(jiǎn)記為A.

注1按點(diǎn)態(tài)方式定義集合X的所有L-fuzzy子集, 表示為FL(X)={A|A: X→L }=LX, 其構(gòu)成完備的Heyting代數(shù)[2,8].

定義2[4]設(shè)X∈Ob(Set), 若集值函數(shù)μ: Lop→P (X)滿足:

1) μ(0)=X;

則μ稱為集合X的L-flou子集, 記作(μ,X). 集合X的所有L-flou子集表示為

F lL(X)={μ: L → P (X)|μ滿足1),2)}.

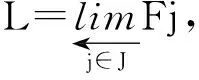
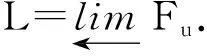
圖1 F上的余錐形Fig.1 Cocone on F

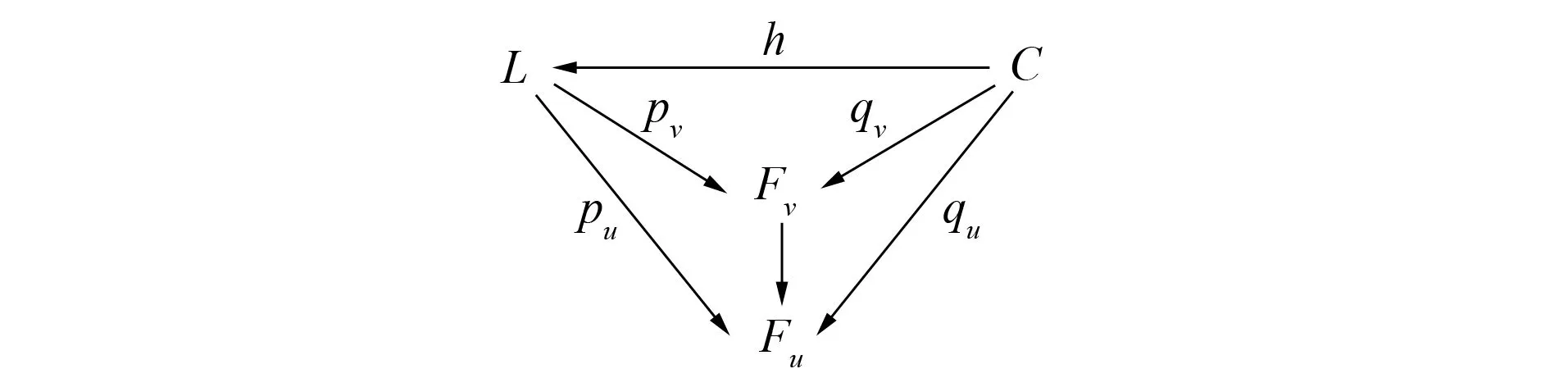
圖2 F的余極限Fig.2 Colimit of F

定義4[9]如果范疇C中任意J型圖都存在極限, 則稱C為完備范疇. 對(duì)偶地, 可定義余完備范疇.

定義5[10]設(shè)C是一個(gè)范疇, 取X∈Ob(C ), 定義范疇C/X如下：

1) 對(duì)象: 任意C∈C, 范疇C中態(tài)射f: C→X作為C/X的對(duì)象;

2) 態(tài)射: 對(duì)于f: C→X, g: D→X, 定義Hom(f,g)={h∈Hom(C,D)|f=gh};

3) 復(fù)合: 由范疇C中復(fù)合誘導(dǎo);

4) 單位: 1f=idX.

則稱范疇C/X為對(duì)象X上的切片范疇. 對(duì)偶地, 可定義余切片范疇X/C.

定義6[8]設(shè)C是一個(gè)完備范疇, L上的一個(gè)C-預(yù)層F是范疇Lop到范疇C的函子F: Lop→C, 則：

1) 對(duì)象間的對(duì)應(yīng): 若u∈Ob(L ), 則F(u)∈C;

2) 態(tài)射間的對(duì)應(yīng): 若v≤u∈Mor(L ), 則F(v≤u): F(u)→F(v)∈Mor(C ).

定義7[8]設(shè)F是L上的一個(gè)C-預(yù)層, {ui|i∈I}, {u=∨ui|i∈I}(ui∈L ), 如果

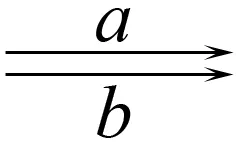
正合, 即態(tài)射e是態(tài)射a,b的等值子, 則稱F是L上的一個(gè)C-層.

注2特別地, 取范疇C為Set, 則可得集合范疇上的預(yù)層及層.

2 范疇Set(L )與范疇Set(fL )的同構(gòu)關(guān)系

定義8設(shè)L是一個(gè)完備格范疇, Set是集合范疇, 則L-fuzzy集合范疇Set(L )定義如下:

1) 對(duì)象: 序?qū)?X,A), 其中X∈Ob(Set), A: X→L為集合X的L-fuzzy子集;

2) 態(tài)射: 序?qū)?f,f*): (X,A)→(Y,B), 其中f: X→Y, f*: A→B由f誘導(dǎo)且滿足A≤B°f;

3) 復(fù)合: 集合映射的復(fù)合誘導(dǎo);

4) 單位: 對(duì)任意對(duì)象(X,A), 有1(X,A)=(1X,1A).

注3由定義3及文獻(xiàn)[11-12], 可定義范疇Set(L )中的極限及余極限等相關(guān)概念.

定義9設(shè)L是一個(gè)完備格范疇, Set是集合范疇, 則L-flou集合范疇Set(fL )定義如下:

1) 對(duì)象: 對(duì)(μ,X), 其中X∈Ob(Set), μ: L→P (X)為集合X的L-flou子集;

3) 復(fù)合: 若φ: (μ,X)→(ν,Y), ψ: (ν,Y)→(ω,Z), 則ψ°φ: (μ,X)→(ω,Z)滿足

(φ*°ψ*)°μ=(φ°ψ)*°μ≤ω;

4) 單位: 對(duì)任意對(duì)象(X,A), 有1(X,A)=(1X,1A).

注4可將L-flou集合范疇Set(fL )視為函子范疇, 即

其中X的冪集合P (X)可視為偏序范疇, 其對(duì)象為集合X的子集合, 態(tài)射為集合間的包含關(guān)系.

定理1設(shè)L是一個(gè)完備格范疇, Set是集合范疇, 則L-fuzzy集合范疇Set(L )同構(gòu)于L-flou集合范疇Set(fL ).

證明: 構(gòu)造從范疇Set(L )到范疇Set(fL )的函子F: Set(L)→Set(fL ), 證明其作用在對(duì)象類上同構(gòu)且局部單與局部滿. 設(shè)函子F: Set(L )→Set(fL ), 則：

1) 對(duì)象間的對(duì)應(yīng): 若A∈Ob(Set(L )), 則F(A)=μA∈Ob(Set(fL )), 這里μA(u)={x∈X|A(x)≥u, u∈L };

2) 態(tài)射間的對(duì)應(yīng): 若f*: A→B∈Mor(Set(L )), 則F(f*)=μf*: μA→μB∈Mor(Set(fL )).

首先證明F作用在范疇Set(L )的對(duì)象到范疇Set(fL )的對(duì)象上是同構(gòu)的. 對(duì)任意μA∈Ob(Set(fL )), 令A(yù)μ∈Ob(Set(L )), Aμ(x)=∨{v∈Ob(L )|x∈μ(v)}. 為簡(jiǎn)便, 記{v∈Ob(L )|x∈μ(v)}=Ix.

首先，對(duì)于城市居民來說，判斷他們與外來人口社會(huì)距離的大小其實(shí)很簡(jiǎn)單，那就是利益的重合。如果她們的利益與遷移人口沒有重合，也就是說他們的利益不會(huì)受到影響時(shí)，社會(huì)距離就比較小；相反，當(dāng)城市居民覺得自身的利益會(huì)受到外來遷移人口的影響而有所損失時(shí)，就會(huì)排斥遷移者，從而有著較大的社會(huì)距離。體現(xiàn)在本次研究中，就是那些有著更高的收入和主觀社會(huì)經(jīng)濟(jì)地位的城市居民與外來遷移人口的社會(huì)距離更近。因?yàn)橄鄬?duì)于外來遷移人口，他們有著無法比擬的競(jìng)爭(zhēng)優(yōu)勢(shì)，而那些收入較少、主觀社會(huì)經(jīng)濟(jì)地位低，再加上年齡較大的城市居民則更容易體會(huì)到來自外來遷移人口的競(jìng)爭(zhēng)，因此對(duì)他們有所排斥。

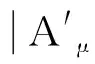
{x∈X|A(x)≥A(x0)=A′(x)≥A(x0)},

從而A′(x0)≥A(x0). 又{x∈X|A(x)≥A′(x0)=A′(x)≥A′(x0)}, 進(jìn)而A(x0)≥A′(x0), 故A′=A. 綜上, F是單的.

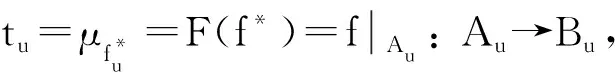
對(duì)任意v≤u∈Ob(L ), t對(duì)應(yīng)如圖4所示的分支之間的交換性. 由圖3的交換性可得圖4的交換性, 故t: μA→μB∈Mor(Set(fL )).

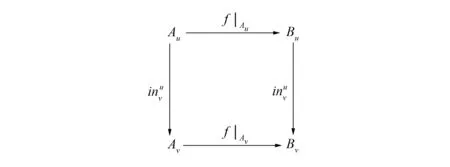
圖3 交換圖Fig.3 Commutative diagram

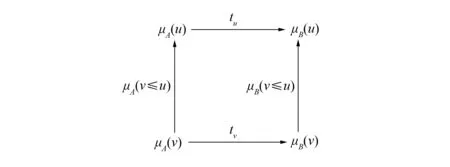
圖4 自然變換t的u,v分支Fig.4 Components u,v of natural transformation t

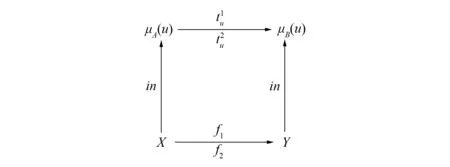
圖5 自然變換t的u,0分支Fig.5 Components u,0 of natural transformation t

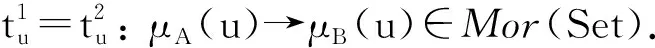
A1,μ=∨{v∈Ob(L )|x∈μA(v)=A2,μ},

故f1*=f2*.

2) 證F局部滿. 令

Aμ(x)=∨{u∈Ob(L )|x∈μA(v)},

Bμ(x)=∨{u∈Ob(L )|f(x)∈μB(v)},

可得

故(f,f*): (X,A)→(Y,B)∈Mor(Set(L )).

綜上, 函子F是從范疇Set(L )到范疇Set(fL )的同構(gòu)函子.

3 L-子對(duì)象與層

定義10[9]設(shè)C是一個(gè)完備范疇, 如果對(duì)任意Z∈Ob(C )及f,g: Z→X∈Mor(C ), 由if=ig, 有g(shù)=h, 則稱i: X→Y∈Mor(C )為單態(tài)射.

考慮(X′,i), 其中X′∈Ob(C ), i: X′→X∈Mor(C )是單態(tài)射.

定義11[9]如果存在f: X′→X″∈Mor(Set), 使得j°f=i成立, 則(X′,i)≤(X″,j). 若g: X″→X′∈Mor(Set), 使得i°g=j,j°f=i, 則稱(X′,i)與(X″,j)等價(jià), 記作(X′,i)～(X″,j).

定義12[9]序?qū)?X′,i)在等價(jià)關(guān)系～下的等價(jià)類稱為X的子對(duì)象. 在不混淆的情形下, 用(X′,i)表示X的一個(gè)子對(duì)象, 其中i: X′→X是單態(tài)射.

命題1[9]設(shè)X∈Ob(C ), X的所有子對(duì)象構(gòu)成的范疇記作Sub(X), 則：

1) 對(duì)象: X的子對(duì)象(X′,i)；

2) 態(tài)射: f: (X′,i)→(X″,j), 且i=j°f;

3) 復(fù)合: 對(duì)于f: (X′,i)→(X″,j), g: (X″,j)→(X?,k), 有g(shù)°f: (X′,i)→(X?,k), 且i=k°(g°f)；

4) 單位: 1f= id(X′,i).

定義13設(shè)X∈Ob(C ), X的L-子對(duì)象是指函子μ: L→Sub(X)滿足:

1) μ(0)=X;

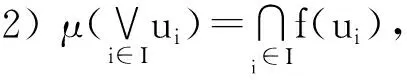
注6當(dāng)X∈Ob(Set)時(shí), X的L-子對(duì)象即為X的L-子集.

定義14[6]設(shè)X∈Ob(Set), 函子F: Lop→Sub(X)是Sub(X)層, 則稱F是X上的一個(gè)層結(jié)構(gòu), (X,F )稱為賦予層結(jié)構(gòu)的集合.

定義15賦予層結(jié)構(gòu)的集合范疇SetL(S H )定義如下：

1) 對(duì)象: 賦予層結(jié)構(gòu)的集合(X,F )；

2) 態(tài)射: (X,F ), (Y,G)賦予層結(jié)構(gòu)的集合, 態(tài)射(f,t): (X,F )→(Y,G)中f: X→Y∈Mor(Set), t: F→G是自然變換;

3) 復(fù)合: (f,t)°(g,s)=(f°g,t°s);

4) 單位: 1(X,F )=(1X,1F).

定理2設(shè)L是一個(gè)完備格范疇, 則賦予層結(jié)構(gòu)的集合范疇SetL(S H )同構(gòu)于L-flou集合范疇Set(fL ).

證明: 由文獻(xiàn)[6]知, 賦予層結(jié)構(gòu)的集合范疇SetL(S H )同構(gòu)于L-fuzzy集合范疇Set(L ). 再由定理1可得結(jié)論.