左截?cái)嘤覄h失數(shù)據(jù)下分位數(shù)差的估計(jì)
荀 立, 崔世崇, 朵 蘭
(長(zhǎng)春工業(yè)大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 長(zhǎng)春 130012)
左截?cái)嘤覄h失(LTRC)數(shù)據(jù)在生物醫(yī)學(xué)、 工程壽命試驗(yàn)、 勞動(dòng)力經(jīng)濟(jì)和保險(xiǎn)精算等領(lǐng)域應(yīng)用廣泛. 對(duì)于這類數(shù)據(jù), 由于觀測(cè)到的數(shù)據(jù)不完全, 因此一般采用乘積限方法估計(jì)感興趣變量的分布函數(shù). 分布函數(shù)乘積限估計(jì)的反函數(shù), 稱為乘積限分位函數(shù). 兩個(gè)分位數(shù)的差稱為分位數(shù)差, 分位數(shù)差也可表示感興趣分布的離散程度, 比標(biāo)準(zhǔn)差更穩(wěn)健. 對(duì)于中位數(shù)對(duì)稱的兩個(gè)分位數(shù)差, 可以用來分析感興趣分布的對(duì)稱程度.
在右刪失數(shù)據(jù)下, 文獻(xiàn)[1]基于Kaplan-Meier乘積限研究了分位數(shù)差的估計(jì)及其漸近性質(zhì); 文獻(xiàn)[2]利用光滑經(jīng)驗(yàn)似然方法得到了分位數(shù)差的置信區(qū)間. 對(duì)于LTRC數(shù)據(jù), 文獻(xiàn)[3-4]討論了分位剩余壽命的差和比的統(tǒng)計(jì)推斷問題; 文獻(xiàn)[5]基于Tsai-Jewell-Wang(TJW)乘積限, 研究了分位數(shù)差的估計(jì)及其大樣本性質(zhì); 文獻(xiàn)[6]進(jìn)一步計(jì)算了分位數(shù)差估計(jì)的強(qiáng)收斂速度和均方收斂速度. 由于TJW乘積限估計(jì)是階梯函數(shù), 因此對(duì)應(yīng)的乘積限分位函數(shù)也是階梯函數(shù). 如果總體分位函數(shù)連續(xù), 則用連續(xù)函數(shù)估計(jì)連續(xù)的總體分位函數(shù)更易表達(dá)感興趣變量的性質(zhì). 因此, 文獻(xiàn)[7]通過對(duì)乘積限分位函數(shù)進(jìn)行光滑處理, 提出了光滑分位函數(shù).
本文通過對(duì)文獻(xiàn)[7]的光滑分位函數(shù)做差, 得到總體分位數(shù)差的一個(gè)光滑估計(jì), 利用經(jīng)驗(yàn)過程的相關(guān)理論, 研究光滑分位數(shù)差估計(jì)的相合性、 漸近正態(tài)性等大樣本性質(zhì). 進(jìn)一步, 在均方誤差的意義下, 與TJW 乘積限分位函數(shù)的差進(jìn)行比較. 數(shù)值模擬結(jié)果表明: 在均方誤差意義下, 當(dāng)窗寬的取值低于0.05或高于0.25時(shí), 根均方誤差比出現(xiàn)負(fù)值, 即此時(shí)的光滑估計(jì)沒有統(tǒng)計(jì)優(yōu)越性; 當(dāng)窗寬在0.05~0.25內(nèi)取值時(shí), 光滑分位數(shù)差的估計(jì)效率比乘積限分位數(shù)差的估計(jì)效率高, 但光滑分位數(shù)差犧牲了估計(jì)的無偏性, 而且由于核函數(shù)的性質(zhì), 光滑分位數(shù)差估計(jì)仍是總體分位數(shù)差的漸近無偏估計(jì).
1 預(yù)備知識(shí)

其中Z(n)=max{Z1,…,Zn}.



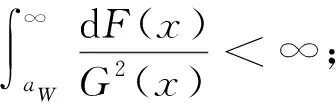
(H2)k(·)是[-1,1]上的概率密度函數(shù), 對(duì)于整數(shù)r≥2, 有
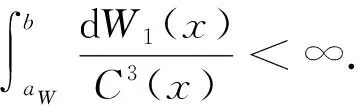
例1設(shè)F(x)=1-e-x,H(x)=1-e-x,G(x)=1-e-2x,k(x)=I[-1,1](x)/2, 則有:
1)W(x)=1-e-2x,aG=aW>0,bG=bW=∞, 進(jìn)而有e-aW<1. 由于(1-y2)-2在[0,e-aW]上是連續(xù)、 有界、 單調(diào)遞增的函數(shù), 所以
2)k(x)為[-1,1]上的概率密度函數(shù), 且r=2.
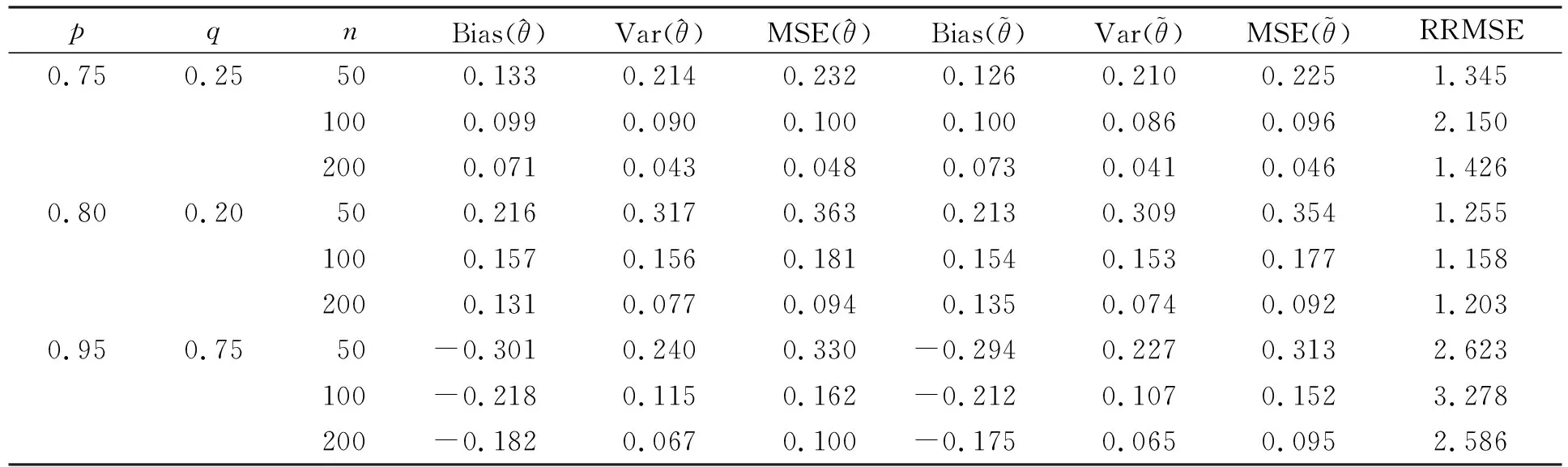
命題1[9-10]若aG≤aW, 對(duì)某些b 其中: 2) 對(duì)λ>0,ε>0,C(z)≥ε及某個(gè)常數(shù)K, 有 命題2[11]?ε>0,F在[Q(p1)-ε,Q(p2)+ε]上兩次連續(xù)可導(dǎo), 0 (1) 證明: 由命題2, 有 由命題1及文獻(xiàn)[10]中推論2.2知, 因?yàn)閒(Q(p))>0和f(Q(q))>0, 所以 對(duì)某個(gè)ξ1,ξ2: 0≤ξ1,ξ2≤1, 有 其中Q(r)(·)為Q(·)的r階導(dǎo)函數(shù). 由條件(H2), 有 其中 (2) 因?yàn)?/p> 由條件(H2)和中心極限定理, 有 其中式(2)成立. 由定理1的證明, 有 從而結(jié)論得證. 其中:kf(·)為一個(gè)核函數(shù); {an}n≥1是一個(gè)正的窗寬列, 當(dāng)n→∞時(shí), 有an→0,nan→∞. 情形1) 50%刪失率和50%截?cái)嗦? 其中F(x)=1-e-x,H(x)=1-e-x,G(x)=1-e-2x; 情形2) 30%刪失率和25%截?cái)嗦? 其中F(x)=1-e-x,H(x)=1-e-3x/7,G(x)=1-e-30x/7. 選用高斯核函數(shù), 窗寬列為hn=…,0.05,0.08,0.10,0.12,0.15,0.18,0.20,0.22,0.25,…, 水平(p,q)=(0.75,0.25),(0.80,0.20),(0.95,0.75), 樣本容量n=50,100,200, 重復(fù)模擬500次, 計(jì)算兩個(gè)分位數(shù)差估計(jì)的根均方誤差比 其中估計(jì)的偏差、 方差和均方誤差分別記為Bias(·),Var(·)和MSE(·). 從偏差、 方差和均方誤差三方面比較兩個(gè)估計(jì)的效率, 其中根均方誤差比表示均方誤差意義下光滑估計(jì)提高的效率. 在上述兩種不同刪失率和截?cái)嗦氏? 窗寬分別為hn=0.05,0.15,0.25的數(shù)值模擬結(jié)果分別列于表1~表6. 表1 刪失率為50%、 截?cái)嗦蕿?0%、 窗寬為0.25的數(shù)值模擬結(jié)果 表2 刪失率為30%、 截?cái)嗦蕿?5%、 窗寬為0.25的數(shù)值模擬結(jié)果 表3 刪失率為50%、 截?cái)嗦蕿?0%、 窗寬為0.15的數(shù)值模擬結(jié)果 由表1可見: 兩個(gè)估計(jì)的偏差、 方差和均方誤差幾乎都隨樣本容量的增大而減小; 光滑估計(jì)的偏差普遍大于乘積限分位數(shù)差估計(jì)的偏差, 因?yàn)楣饣椒奚斯烙?jì)的無偏性; 但光滑估計(jì)是漸近無偏的; 光滑分位數(shù)差估計(jì)的方差和均方誤差都比乘積限分位數(shù)差估計(jì)值小, 表明此時(shí)在方差和均方誤差意義下, 光滑方法提高了估計(jì)效率; 根均方誤差比表示估計(jì)效率提高的比值, 例如, 樣本容量為50的四分位差θ(0.75,0.25)的兩個(gè)估計(jì), 光滑方法將估計(jì)效率提高了1.609%, 對(duì)于更大的分位數(shù)差θ(0.80,0.20)和尾部分位數(shù)差θ(0.95,0.75)也有類似結(jié)果. 表2中分位數(shù)差θ(0.80,0.20)的兩個(gè)估計(jì)的根均方誤差比出現(xiàn)負(fù)值, 表明此時(shí)乘積限分位數(shù)差估計(jì)比光滑分位數(shù)差估計(jì)更有效, 光滑方法不具有統(tǒng)計(jì)優(yōu)越性. 表4的刪失率和截?cái)嗦逝c表3不同, 但得到了與表3類似的結(jié)果, 表明在適當(dāng)選擇的窗寬下, 不同的刪失率和截?cái)嗦蕦?duì)估計(jì)效率的提高無影響. 表5的結(jié)果類似表1, 對(duì)于刪失率為50%、 截?cái)嗦蕿?0%、 窗寬為0.05的情形, 仍然有光滑分位數(shù)差估計(jì)的效率高于乘積限分位數(shù)差估計(jì)的結(jié)果. 表6的結(jié)果類似表2, 表明窗寬為0.05時(shí), 光滑分位數(shù)差的估計(jì)效率并不比乘積限分位數(shù)差估計(jì)的效率高. 表4 刪失率為30%、 截?cái)嗦蕿?5%、 窗寬為0.15的數(shù)值模擬結(jié)果 表5 刪失率為50%、 截?cái)嗦蕿?0%、 窗寬為0.05的數(shù)值模擬結(jié)果 表6 刪失率為30%、 截?cái)嗦蕿?5%、 窗寬為0.05的數(shù)值模擬結(jié)果 上述結(jié)果表明: 窗寬高于0.25或低于0.05時(shí), 根均方誤差比出現(xiàn)負(fù)值, 此時(shí)光滑分位數(shù)差沒有統(tǒng)計(jì)優(yōu)越性; 當(dāng)窗寬在0.05~0.25內(nèi)取值時(shí), 根均方誤差比大于0, 說明此時(shí)光滑分位數(shù)差估計(jì)比乘積限分位數(shù)差估計(jì)具有更高的效率. 注1本文根據(jù)文獻(xiàn)[7]的光滑分位函數(shù)定義總體分位數(shù)差的估計(jì)量, 并與文獻(xiàn)[5]定義的乘積限分位數(shù)差估計(jì)比較估計(jì)效率, 所有理論證明均在截?cái)嘧兞俊?壽命變量、 刪失變量相互獨(dú)立的條件下進(jìn)行. 對(duì)于壽命變量與刪失變量相依的情形, 根據(jù)文獻(xiàn)[12], 產(chǎn)生長(zhǎng)度偏差右刪失(LBRC)數(shù)據(jù), 考慮LBRC數(shù)據(jù)下樣本分位數(shù)差的估計(jì). 用本文方法, 在均方誤差意義下, 選擇適當(dāng)?shù)拇皩? 得到類似估計(jì)效率的改善結(jié)果列于表7~表11. 表7 刪失率為50%的LBRC數(shù)據(jù)下窗寬為0.25的數(shù)值模擬結(jié)果 表8 刪失率為30%的LBRC數(shù)據(jù)下窗寬為0.25的數(shù)值模擬結(jié)果 表9 刪失率為50%的LBRC數(shù)據(jù)下窗寬為0.15的數(shù)值模擬結(jié)果 表10 刪失率為30%的LBRC數(shù)據(jù)下窗寬為0.15的數(shù)值模擬結(jié)果 表11 刪失率為50%的LBRC數(shù)據(jù)下窗寬為0.05的數(shù)值模擬結(jié)果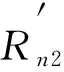

2 主要結(jié)果

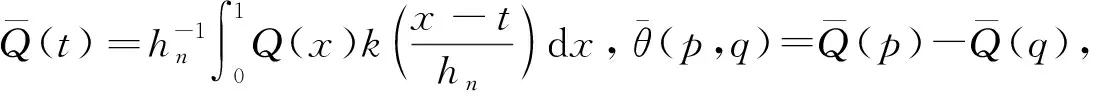






3 數(shù)值模擬與分析