基于時變增益ESO的多航天器SO(3)姿態協同控制

馬鳴宇， 董朝陽， 王青， 周敏

(1. 北京航空航天大學航空科學與工程學院, 北京 100083； 2. 北京電子工程總體研究所， 北京 100854；3. 北京航空航天大學自動化科學與電氣工程學院, 北京 100083； 4. 航天系統仿真重點實驗室 北京仿真中心， 北京 100854)

多航天器姿態協同是指通過設計恰當的協同控制律，利用航天器之間的信息交互使得各航天器姿態保持一致。在航天器控制領域，姿態協同具有廣泛的應用前景。多顆小衛星通過對衛星間的相對姿態進行協調，可以協同工作完成復雜的任務，具有成本低、研制周期短、應用方式靈活等優點[1]；在航天器交會對接、衛星捕獲等航天作業中，姿態協同也是一項關鍵技術，具有重要的研究意義[2-3]。因此，多航天器系統的協同控制問題得到越來越多的重視和研究[4-6]。

對于單個航天器的姿態控制問題，國內外學者采用自適應控制[7]、魯棒控制[8]、滑模控制[9]等多種方法進行了研究，取得了豐富的研究成果。在上述方法中，航天器的姿態大多采用的是歐拉角、四元數[10]或羅格里德參數模型[11]，在姿態運動范圍較小時可以取得良好效果，但仍存在一定的局限性。歐拉角模型在姿態角全局范圍變化時會出現奇異，導致基于這種方法設計的控制器也只適用于某個范圍內；采用四元數進行姿態表示的方法能夠避免奇異，但其與旋轉矩陣的映射不具有唯一性，用于控制時可能導致姿態散開，引起系統性能下降[12]；羅格里德參數模型同樣存在非全局與不唯一性。為了解決這些問題，文獻[13-14]提出了基于特殊正交群(Special Orthogonal Group，SO(3))的姿態建模與控制方法。SO(3)與旋轉矩陣是一一對應的，滿足姿態描述的全局性，相比傳統區分通道分別設計的方法更為統一，且不存在奇異問題。針對個體控制問題，SO(3)方法已經取得了一定的研究和應用成果。文獻[14-15]采用旋轉矩陣對航天器姿態進行建模，克服了姿態展開現象。文獻[16]詳細討論了單剛體的SO(3)姿態跟蹤控制問題，保證了系統的全局指數穩定性。

另外，在實際復雜的環境中，航天器系統不可避免地會受到干擾，而干擾會造成系統的穩定性能和協同效果下降。文獻[17-18]分別考慮了存在執行器安裝偏差和不確定性情形，提出了航天器魯棒控制方法，屬于對干擾的被動抑制。針對干擾的主動抑制控制，以擴張狀態觀測器(Extended State Observer, ESO)為核心的自抗擾控制方法近年來得到越來越多的關注。ESO將系統的不確定性和干擾等效為總干擾，以其作為擴張狀態進行實時估計，進而在控制器設計中可以針對系統的總干擾進行補償，提高系統的抗干擾能力。ESO的穩定性分析相對復雜，目前主要基于Lyapunov理論開展。文獻[19]證明了可以通過嚴格構造Lyapunov函數完成對常值增益的線性ESO的收斂性分析。而對于非線性ESO則需要假設Lyapunov函數存在[20]，不便于控制器設計和穩定性分析。因此在后續研究中，線性ESO已經得到了一定的實際應用[21-23]。但需要注意的是，線性常值增益ESO在初值和系統初值不一致時，經常會出現峰化現象(peaking phenomenon)[24-25]，對系統造成不利影響。

相比單個航天器，多航天器控制系統更為復雜[26]。而對于多航天器系統的SO(3)建模、ESO設計以及協同控制問題，目前研究還比較有限。除了個體動力學外，航天器之間的通信拓撲也會對系統的整體行為產生影響。在多航天器SO(3)控制中，需要根據拓撲結構設計恰當的SO(3)形式的協同指令。同時，由于SO(3)模型中姿態采用矩陣而非向量表示，因此針對SO(3)模型的ESO也需要重新設計和分析。

考慮到上述問題，本文將SO(3)姿態描述引入到多航天器系統，結合航天器之間的有向通信拓撲建立其協同控制模型。在此SO(3)模型上設計了一種時變增益ESO對系統的總干擾進行估計，在保證觀測誤差收斂的同時，削弱常值ESO的峰化現象。進一步，利用相鄰航天器的信息構造了SO(3)形式的協同控制指令，并設計了對應的協同控制器，從理論上證明了閉環系統的穩定性，所提出的方法能夠實現干擾情形下多航天器系統的有效協同。以5個包含不同干擾和不確定性的航天器系統進行了仿真，驗證了理論分析結果。

1 多航天器姿態模型建立

1.1 航天器姿態SO(3)模型

在三維空間中，姿態代表了航天器本體坐標系與慣性坐標系之間的旋轉關系，而坐標系之間的旋轉變換可以用一個正交變換矩陣R來表示，所有的正交變換矩陣構成了SO(3)群：

SO(3)={R∈R3×3|RRT=I3,detR=1}

(1)

任意姿態都與特定矩陣R∈SO(3)一一對應。因此，可以考慮采用SO(3)中對應的元素R來表示航天器的姿態。令Ω=[ω1ω2ω3]T，定義運算

(2)

為hat映射。hat映射的逆運算∨稱為vee映射，其將任意三維反對稱陣映射為三維向量，即

(3)

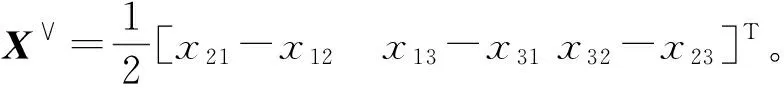
(4)

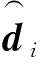
對式(4)進行展開后處理可得

(5)

(6)

對于干擾di，有如下假設[19-20]。

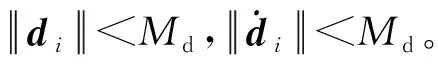
1.2 多航天器通信拓撲描述

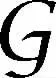
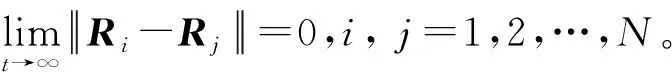
2 線性時變增益ESO設計

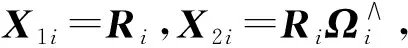
(7)

(8)

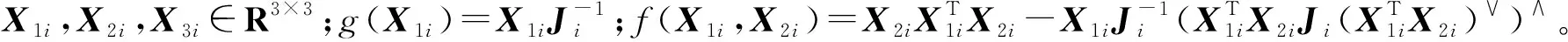
對于式(8)所示系統，考慮設計以下形式的ESO：

(9)

式中：Lki(t)=diag{lki(t),lki(t),lki(t)}，lki(t)為時變增益系數，k=1,2,3。

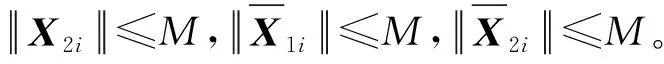
(10)

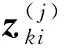
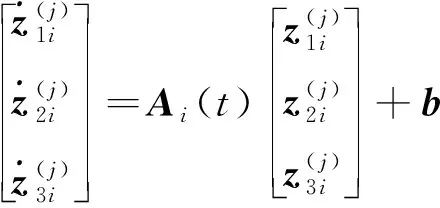
(11)

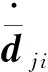
為了分析系統式(11)的穩定性，將其轉換為標準型：

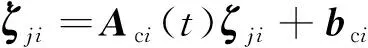
(12)

式中：

其中：aki(t)為與lki(t)有關的函數，且滿足以下假設。

假設3aki(t)有界且三階連續可導，k=1, 2,3。

(13)

同理，與系統式(12)對應的可控性矩陣為

(14)

則系統式(11)到系統式(12)的坐標變換矩陣為

(15)

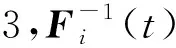
(16)

(17)

由Fi(t)、bi和bci的表達式以及式(17)中的第1個式子可以得出：

(18)

由式(18)可知，lki(t)能夠表示為aki(t)的函數，即可以通過設計aki(t)來保證系統式(12)穩定，進而保證ESO的穩定性。在確定合適的aki(t)后，ESO的參數也隨之確定。于是，考慮與系統式(12)對應的PD特征值和SD特征值分別為ρki(t)和μki(t)[25,27]，定義：

T0i(t)=T1i(t)=1

(19)

(20)

T3i(t)=

(21)

則有如下關系成立：

(22)

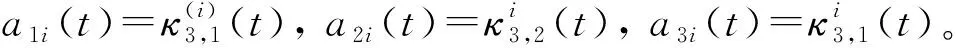
引理1設ρki(t)為實數且滿足如下條件:

1)ρki(t)有界且三階連續可導；

2) 由式(19)～式(22)得到的aki(t)滿足假設3；

3) 存在常數c>0，使得ρki(t)≤-c<0。

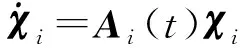
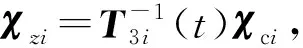
(23)

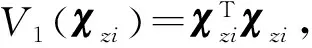
(24)

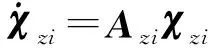
考慮χci和χi系統的狀態轉移矩陣分別為Φχci(t,t0)和Φχi(t,t0)，同理可得

(25)

(26)

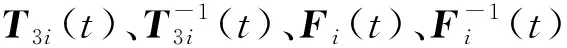
(27)

(28)

從而證明了χi和χci是指數穩定的。

證畢

在此基礎上，關于觀測誤差的穩定性有如下定理成立。

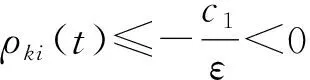
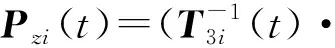
Azi(t)χzi

(29)

式中：

Azi(t)=

(30)

由此可知：

(31)

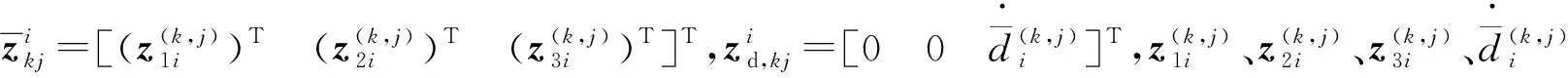
(32)

易知存在常數c2>0，使得

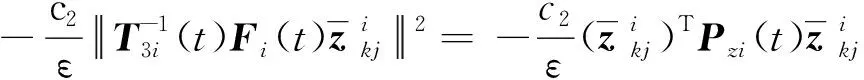
(33)

再根據Pzi(t)的性質可知，存在正常數c3、c4和c5使得：

(34)

從而有

(35)

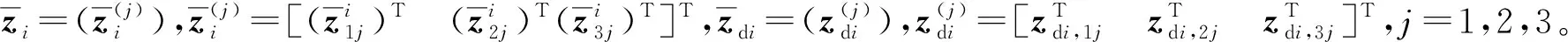
(36)

(37)

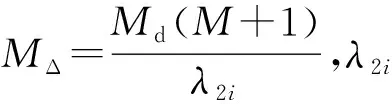
將式(37)代入式(36)，則有

(38)

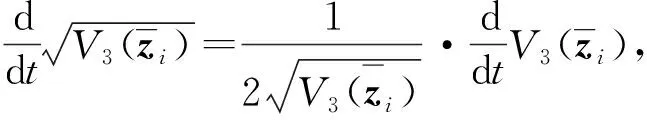
(39)

最終得到

(40)

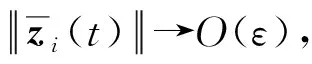
證畢

注1定理1在引理1的基礎上分析了時變增益ESO的收斂性。若ρki(t)取1/ε的同階量，則觀測誤差有界且趨于ε的同階量。同時，在ρki(t)確定后，通過式(18)和式(22)可以計算得到ESO增益lki(t)。

3 SO(3)協同控制器設計

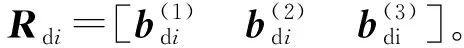
(41)

(42)

(43)

在姿態指令信號Rdi的基礎上，定義SO(3)中的相對姿態誤差和角速度誤差分別為

(44)

(45)

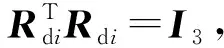
(46)

根據式(45)和式(46)，航天器i的誤差方程可以表示為

(47)

(48)

4 閉環系統協同控制穩定性分析

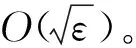
證明選取閉環系統的Lyapunov函數為

(49)

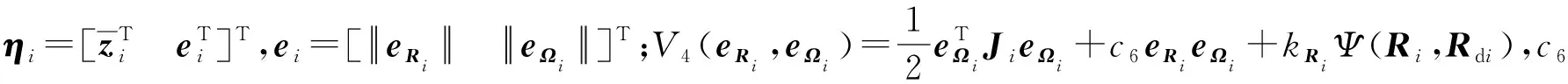
首先證明V4的正定性。易知

(50)

(51)

(52)

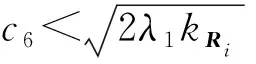
(53)

進一步，考慮式(49)中Ψ(Ri,Rdi)對時間t的導數：

(54)

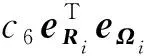
(55)

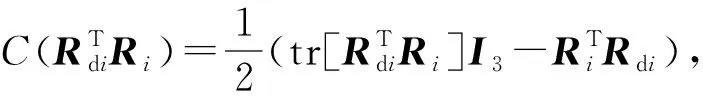
結合式(54)、式(55)對V5(ηi)求導可得

(56)

式中：

(57)

同時，根據前述的分析可知：

(58)

進一步，根據Young不等式，有

(59)

(60)

將上述結果代入式(56)中可得

(61)

式中：

(62)

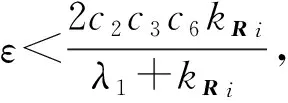
(63)

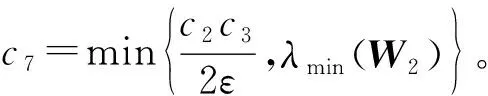
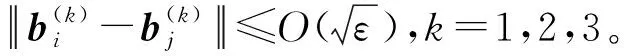
(64)

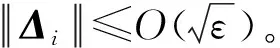
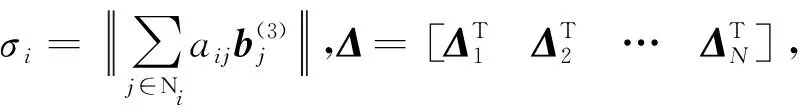
(65)

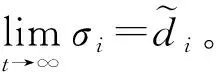
(66)

(67)

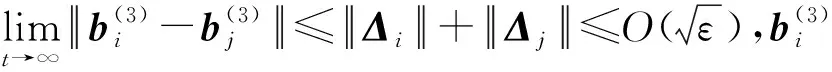
證畢

注2通過航天器模型式(4)和控制器式(48)設計過程可以看出，本文提出的SO(3)協同控制方法允許各航天器具有不同的總體和控制參數，即適用于航天器異構的情況，有利于本文方法在工程中的應用。

5 仿真驗證

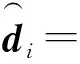
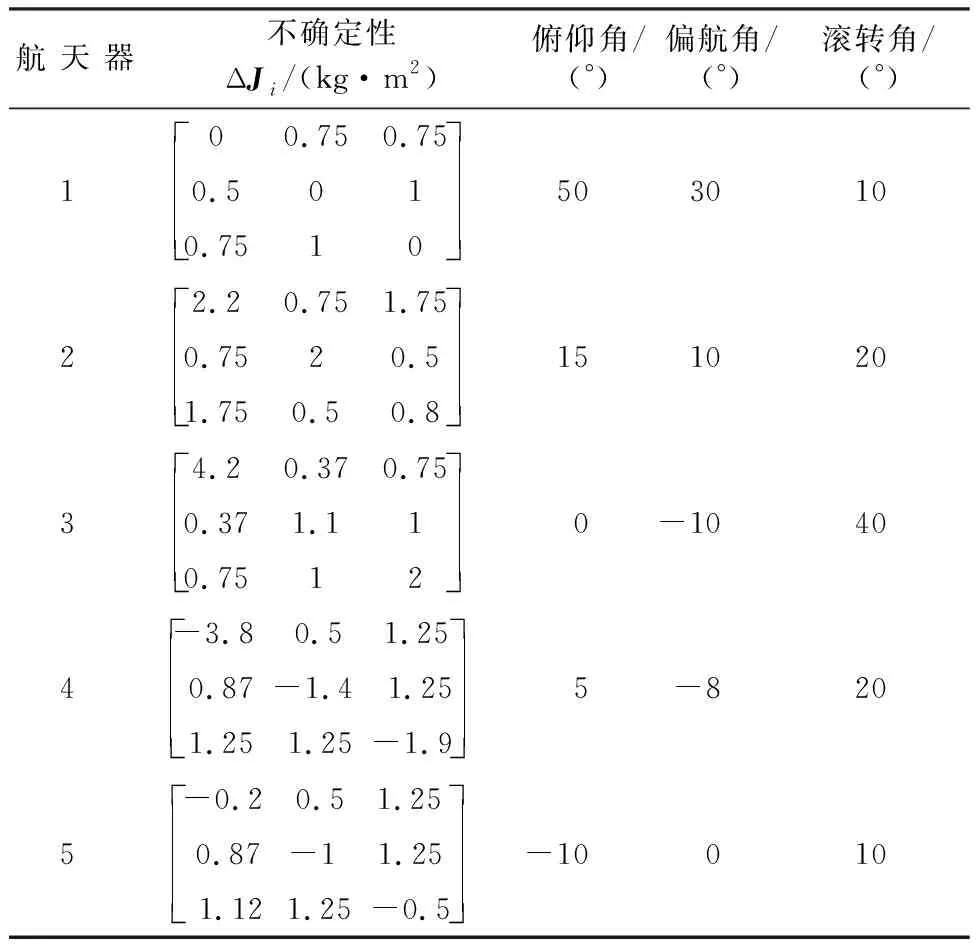
表1 航天器初始條件和參數

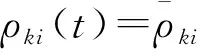
在協同控制器設計與仿真中，均采用R矩陣對航天器姿態進行描述，并基于SO(3)方法完成上述過程。為了便于結果呈現，本文在仿真結果圖中將R轉換為姿態角度進行表示。圖2給出了多個航天器的俯仰、偏航、滾轉角度隨時間變化曲線。可以看出，在存在干擾的情況下，多航天器系統能夠以較快的速度實現穩定的協同，控制效果良好。

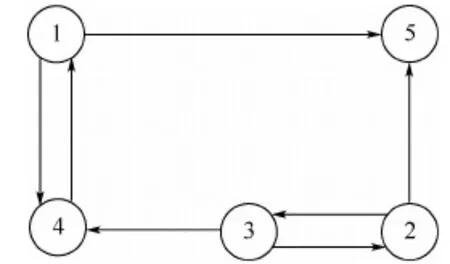
圖1 航天器通信拓撲Fig.1 Communication topology of spacecraft

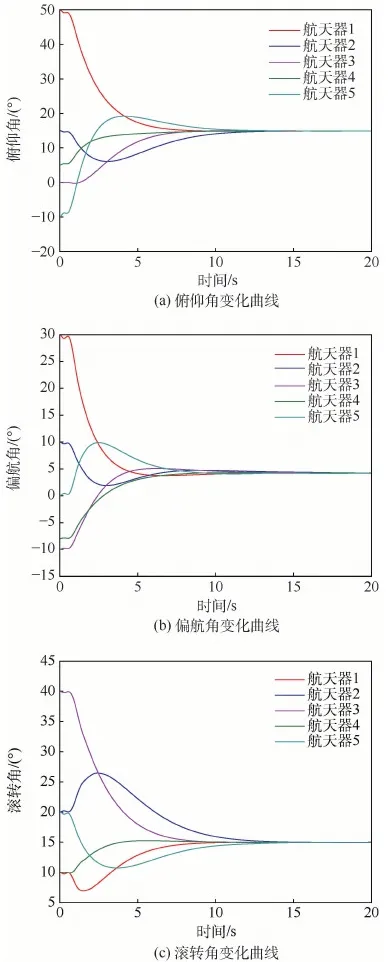
圖2 多航天器姿態角變化曲線Fig.2 Variation curves of attitude angles of multiple spacecraft

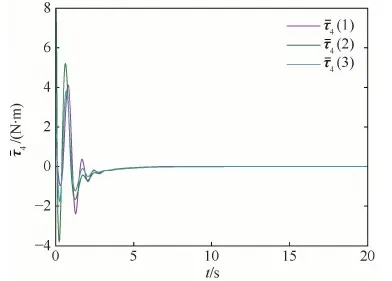
圖3 考慮干擾補償的控制力矩(航天器4)Fig.3 Control moment with disturbance compensation (Spacecraft 4)

進一步，為了定量描述各航天器姿態協同收斂情況，對比說明本文基于SO(3)方法的控制效果，定義：

(68)

式中：qi=ri-r1，ri=[φiψiγi]T，φi、ψi和γi分別為航天器的俯仰角、偏航角和滾轉角。

根據Q的定義可知，若Q趨于0，則表示多航天器實現了姿態協同。在相同初始條件與ESO參數的情況下，文獻[10]采用四元數模型，文獻[11]使用羅格里德參數。從圖5可以看出，文獻[10]方法和文獻[11]方法的Q值收斂到1°的時刻分別為10.87 s和7.26 s，而本文方法為5.88 s，驗證了本文方法的有效性和快速性。

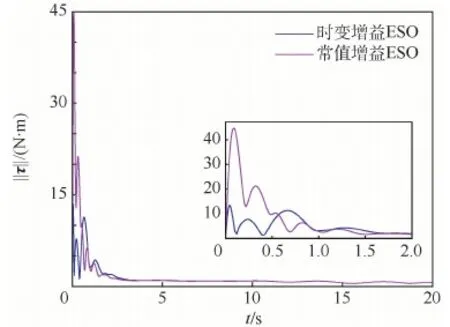
圖4 控制力矩范數對比曲線Fig.4 Comparative curves of norms of control moment

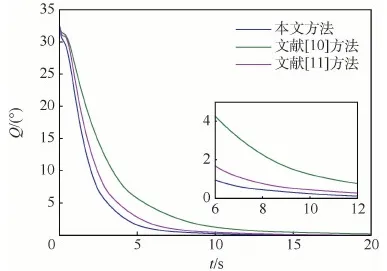
圖5 不同方法Q值變化對比曲線Fig.5 Comparative curves of Q with different methods

6 結 論

本文針對存在干擾情形下的多航天器系統，對其協同控制問題進行了研究。

1) SO(3)能夠從整體的角度對姿態進行描述，結合有向通信拓撲建立了多航天器SO(3)控制模型，并以此提出了相應的控制策略。基于SO(3)方法的協同控制是可行的。

2) 模型不確定性和外部干擾可以等效為系統的總干擾。在此情形下，設計了適用于SO(3)模型的線性時變增益ESO，所提出的時變增益ESO能夠完成對干擾的有效估計。相比常值增益ESO，時變增益ESO可以削弱峰化現象，降低了對控制力矩大小的需求。

3) 設計了SO(3)形式的協同指令，結合ESO可以對干擾進行觀測并在控制器中補償，保證干擾情形下多航天器的協同控制效果。本文給出了穩定性證明過程。

4) 仿真算例結果表明，多航天器系統能夠實現穩定協同，驗證了本文方法的有效性和快速性。