飛機結構拓撲優化方法研究

□ 李英磊 □ 曹宗杰

中國人民解放軍空軍航空大學航空作戰勤務學院 長春 130022

1 研究背景

隨著航空事業的發展，綜合性能更高的航空器才能適應現代戰爭的需求，例如飛機要有良好的氣動性能、較少的材料損耗、較長的使用壽命［1］，且維修方便。目前，要求航空器在研發設計生產中具有結構輕量化、布局智能化、強度最優化的特點［2-5］。

結構優化設計在航空科技領域中廣泛采用的方法主要有尺寸優化、形狀優化和拓撲優化三種［6］。尺寸優化的主要對象是桿件截面積、板殼厚度等，形狀優化的主要對象是結構外觀形狀或者孔洞形狀，拓撲優化則是研究材料分布問題［7］。

拓撲優化設計是機械、電子、力學、控制、仿真、材料、先進制造技術等多學科的交叉耦合，廣泛應用于建筑、機械、兵器科學、飛機制造、載人航天、探月工程等重大領域［8-10］。材料科學和制造工藝的迅猛發展為這種設計方法的實現提供了保障，目前拓撲優化方法已達到實用階段，具有完整的設計體系。

2 拓撲優化分類

拓撲優化是一種在初始拓撲結構未知條件下，尋找材料空間最佳傳力路徑，設計滿足約束條件的最優材料布置形式和結構輕量化的優化方法。拓撲優化按照研究對象的不同，可分為離散結構拓撲優化與連續體結構拓撲優化兩類，筆者研究的飛機結構拓撲優化設計多為連續體結構拓撲優化。筆者重點對比研究目前在飛機結構拓撲優化設計中應用的幾類較常見的方法。

3 飛機結構拓撲優化主要方法

現如今，連續體拓撲優化技術已建立了多準則、多學科和多目標優化設計的基本架構，并在飛機實際結構減重設計中得到應用［11］。

目前常用的連續體拓撲優化方法有均勻化拓撲優化法、變密度拓撲優化法、漸進結構拓撲優化法、變厚度拓撲優化法、獨立連續映射拓撲優化法、水平集函數拓撲優化法［12］。

3.1 均勻化拓撲優化法

1988年，均勻化拓撲優化法作為第一種系統的連續體拓撲優化方法被發表，意味著連續體拓撲優化方法由理論研究轉為實踐應用。均勻化拓撲優化法借助微結構的思想，把較易于理解的尺寸優化概念用于拓撲優化中，即把難度較大的拓撲優化求解問題轉化為難度較小的尺寸優化求解問題。因為在尺寸優化中已知靈敏度，設計修改就非常便捷了，可以在考慮極少影響因素的情況下直接對有限元模型作出對應修改。當用參數方程定義結構形狀時，計算靈敏度與形狀靈敏度的關系可以等價為孔洞尺寸與微小實體結構體積的關系。均勻化拓撲優化模型為：

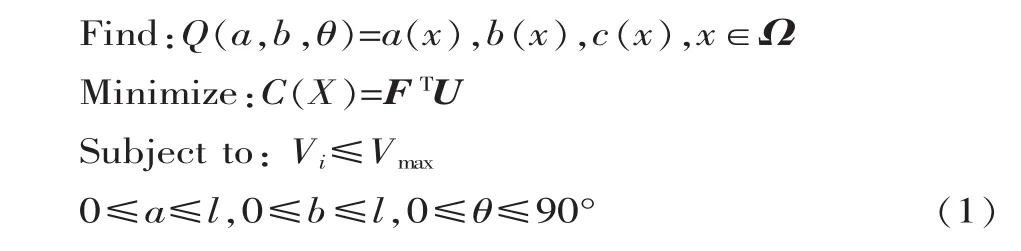
式中：a、b為微小孔洞邊長；l為微小孔洞最大孔洞尺寸；θ為微小孔洞角度；Ω為設計區域；C（X）為結構整體柔度；F結構載荷向量；U為結構節點位移向量；Vi為結構拓撲優化后的體積；Vmax為保留結構最大體積。

3.2 變密度拓撲優化法

1993年，在均勻化拓撲優化法的基礎上，誕生了變密度拓撲優化法。變密度拓撲優化法又稱偽密度拓撲優化法，偽密度的含義是，假設構成結構的材料密度與材料的某一個或幾個物理參數存在函數關系，材料的偽密度可在區間［0，1］之間取值［13］。當拓撲優化模型的偽密度值在［0，1］之間任意連續取值時，若單元處為空孔，則求解后單元的偽密度為0。若單元處為實體，則求解后單元的偽密度為1。若偽密度在0.5附近，則引入冪指數懲罰項對中間值進行懲罰，使其更好地偏向0或1端［14］。變密度拓撲優化模型為：

式中：xi為第i個設計變量；K為結構的整體剛度矩陣；V0為結構的初始體積；f為體積分數；xmin為設計變量所能取得的最小值；xmax為設計變量所能取得的最大值。

3.3 漸進結構拓撲優化法

1993年提出的漸進結構拓撲優化法，其原理為逐步刪除無效與低效率材料來達到拓撲優化的目的［15］。通常，應用漸進結構拓撲優化法時去除材料可采用兩種方法，一種是對應力、應變能量密度函數的彈性模量做調整，另一種是對低應力、低應變能量密度的材料空間做刪減。雙向漸進結構拓撲優化法是在漸進結構拓撲優化法的基礎上得來的，這一方法在刪除低效材料時，采用移除低靈敏度實體單元和增加高靈敏度空單元的方法，實現高應力區域周圍材料的增減［16］。這一方法以簡單設計區域為研究起點，以應力為約束條件，以結構最小質量為優化目標，可以大大減化有限元問題分析過程，并大幅提高計算效率。漸進結構拓撲優化模型為：

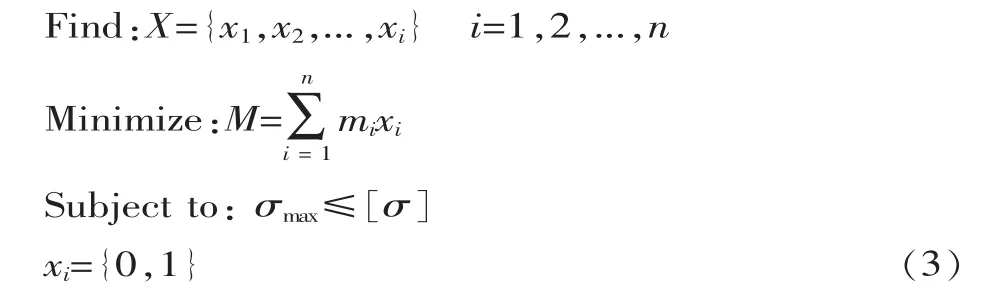
式中：M為總質量；mi為第i個單元的質量；σmax為單元最大應力；［σ］為許用應力。

3.4 變厚度拓撲優化法

1994年，變厚度拓撲優化法首次提出，并應用于薄殼結構分析的拓撲優化問題。顧名思義，變厚度拓撲優化法中的優化變量即為單元厚度，其基本思想為若單元厚度是均勻不變的，可以把復雜連續的拓撲優化變量問題簡化為厚度大小問題。拓撲優化后，可以得到帶有空孔且厚度均勻的平面薄板或平面殼體結構，使用單元厚度閾值進行限定，單元厚度將朝著實體或者空孔進化，最終完成結構的拓撲優化。變厚度拓撲優化模型為：

式中：hi為第i個單元的厚度；V為結構體積；Si為第i個單元的面積；hmax為單元厚度所能取得的最大值。

3.5 獨立連續映射拓撲優化法

獨立連續映射拓撲優化法是在1996年提出的，它摒棄了常用的以結構單元尺寸、面積、厚度和密度等單元特性為設計變量的思想，創新引入變量參數概念來表示單元實體與空心，并且這一變量參數與單元特征無關。

建立獨立連續映射拓撲優化模型，需要用到階躍函數、磨光函數、跨欄函數、過濾函數，用于實現在［0，1］區間上的離散-連續/求解-離散過程。

獨立連續映射拓撲優化法從分布在［0，1］上的由離散變量組成的階躍函數開始優化，取磨光函數逼近階躍函數。因為磨光函數是連續函數，所以采取磨光函數可以盡可能逼近0或1的拓撲變量特性，可使階躍函數連續化，完成離散-連續的過程。

選擇相匹配的優化設計算法，依據待求問題的數學模型與某一閾值的關系，對連續體拓撲優化問題進行求解。

定義階躍函數的逆映射為跨欄函數，磨光函數的逆映射為過濾函數，可將映射在［0，1］區間上的連續變量的優化結果反映至離散的最優設計變量，完成連續-離散的過程。

以結構質量為目標函數，以應力、頻率、位移等為約束條件，獨立連續映射拓撲優化模型可表示為：

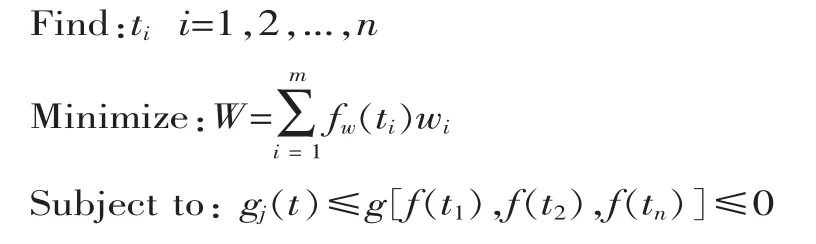
式中：ti為表征第i個單元有無的拓撲變量；W為總質量，wi為第 i個單元的質量； gj（t）為位移、應力、頻率等參數的約束方程；tmin為變量所能取得的最小值。

3.6 水平集函數拓撲優化法

水平集函數拓撲優化法是常見的數值優化方法之一。在2000年，水平集函數拓撲優化法作為處理等應力結構優化的一種有效方法，引入結構拓撲優化中，并且逐步改進應用至高邊界分辨率剛度結構的拓撲優化求解問題領域。水平集函數拓撲優化法把二維或三維結構對應取三維或四維的水平集函數，用零水平集來表示，這樣結構在邊界應力大處向外擴張，即增加材料，在應力小處向內收縮，即刪除材料，這一過程可由水平集函數的變化求解直觀反映。水平集函數φ＝φ（x，t）可表示為：

式中：S為設計區域幾何邊界，即零等值線或面；D為優化過程中結構的改變構型。

以水平集函數φ（x）為設計變量，以整體柔度為目標函數，水平集函數拓撲優化模型可表示為：

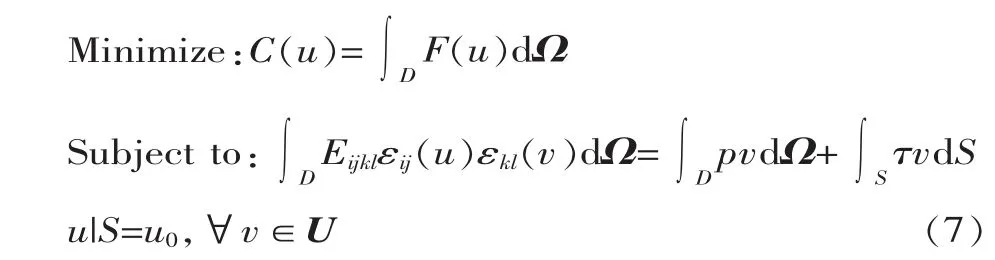
式中：C（u）為水平集設計區域的結構整體柔度；F（u）為結構受力；Eijkl為不同材料的楊氏模量；εij、εkl為不同材料的應變張量；p為體積力；τ為邊界載荷；u為位移；u0為初始位移；v為虛位移。

4 拓撲優化方法特點

傳統的設計過程中，工程師依靠自身經驗或借鑒原有型號飛機結構，初步設定每個元件尺寸大小和位置分布，再通過模擬試驗收集數據，計算校核設計方案的可行性，這種方法往往需要大量煩瑣工作才能達到設計要求。因此，傳統的設計過程一方面會更多地注重結構的強度和壽命等安全性因素，造成減重效果并不理想；另一方面過多依賴工程師個人主觀經驗，會造成一定程度的人力與財物浪費，拖延研發周期，同時缺乏嚴謹的設計準則和依據［17］。

飛機結構拓撲優化設計方法可以較好解決以上問題，以基本力學理論和有限元原理建立數學模型，借助計算機輔助設計理論與計算輔助制造軟件完成對設計要求的設定、運算和分析布置，為新型飛機結構設計定型和已定型飛機結構減重優化提供精確、規范、有利用價值的設計參考方案。

均勻化拓撲優化法通過尺寸的變化來達成結構體的增減，最終完成拓撲優化過程。這一方法為拓撲優化的經典方法，原理成熟，常用于較好地處理病態材料分配問題。

變密度拓撲優化法通過引入偽密度概念，在假設材料密度可變的條件下探究密度與物理屬性間的非線性關系，并以此建模［18］。常用的插值模型有基于人工材料模擬密度基礎提出的以正交各向同性材料指數為懲罰函數的各向同性材料懲罰模型，以及插值函數以有理函數形式建立的材料屬性合理近似模型兩種，實際應用中以各向同性材料懲罰模型較多［19］。

漸進結構拓撲優化法的核心思想是滿應力準則，假設結構中各部分的應力大小均完全相等且接近安全極限。滿應力準則可以保證在拓撲優化迭代中，結構始終保持良好的力學性能，因此在工程實踐中研究與應用廣泛。

變厚度拓撲優化法以厚度為設計變量，數學模型較為簡單且易求解，處理二維平面的拓撲優化問題非常方便。這一方法針對的主要是平面彈性體、薄板和殼體等二維結構，對三維實體結構不適用。

獨立連續映射拓撲優化法使離散變量經過多次映射運算，轉化為求連續變量問題。這一方法得到的模型連續光滑，求解速度和效率均顯著提高，但因為映射方法的求解數值不穩定，在求解邊界處較易形成鋸齒狀、棋盤格現象。

水平集函數拓撲優化法能較好地滿足連續體優化的需求，但局限性也很明顯，初始值依賴性強，每迭代一次需重新計算水平集函數，且在二維問題求解時不能生成孔，邊界優化收斂速度遠慢于其它優化方法，運算時間長。水平集函數拓撲優化法被引入拓撲優化領域較晚，是一種較新型的優化方法，但受上述原因影響，這一方法目前在工程實踐中應用較少。

拓撲優化方法求解時易發生四類影響數值計算結果的問題：棋盤格、多孔材料、網格依賴、局部極值。當出現棋盤格和多孔材料現象時，對可制造性影響較大。當出現網格依賴現象時，對可靠性影響較大。局部極值問題則會引起無全局最優解或無工程可行解［20］。棋盤格和網格依賴現象總是同時出現、同時消失。上述拓撲優化方法各有利弊，表1為拓撲優化方法的對比。

5 總結

介紹了拓撲優化的主要方法和優缺點，總結了拓撲優化模型。針對各方法的應用范圍和特點加以歸納整理。結構拓撲優化在解決工程實際問題中是常用的設計方法，使用拓撲優化設計方法參與飛機的各個結構件乃至整個飛機的結構布局設計，對減輕飛機質量、降低制造成本、節省材料、減少環境和噪聲污染等都有很大作用。

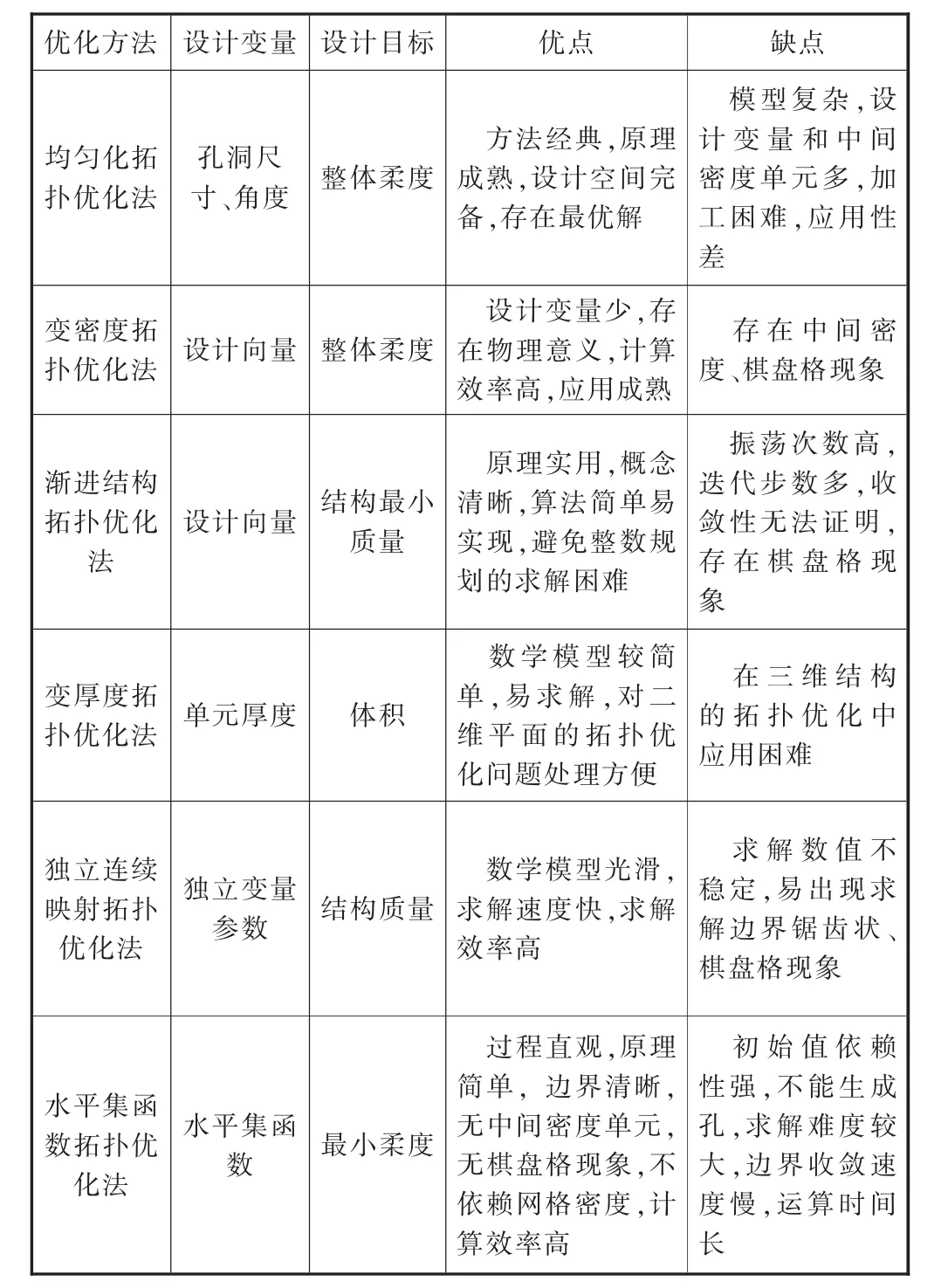
表1 拓撲優化方法對比