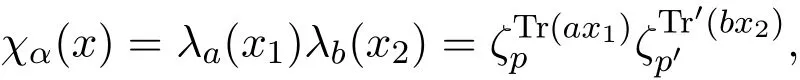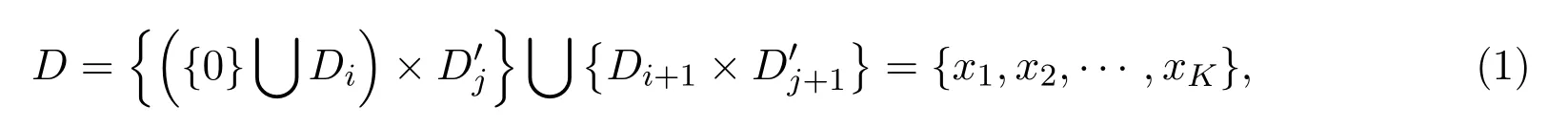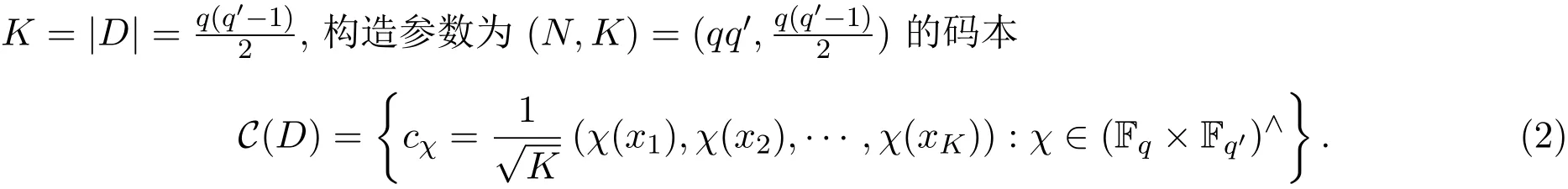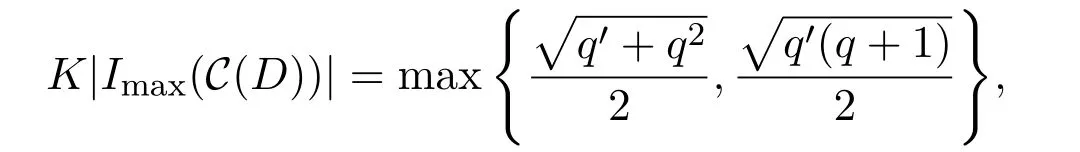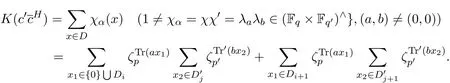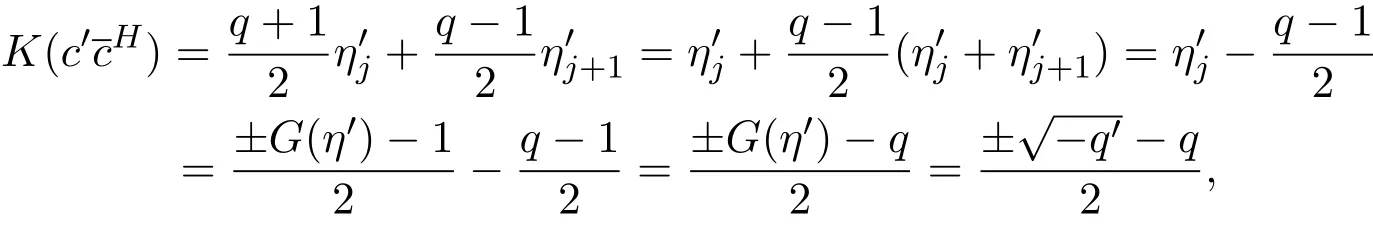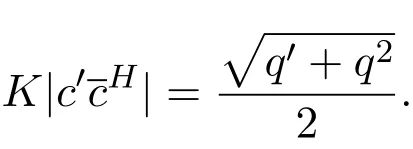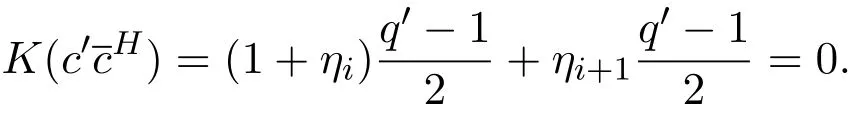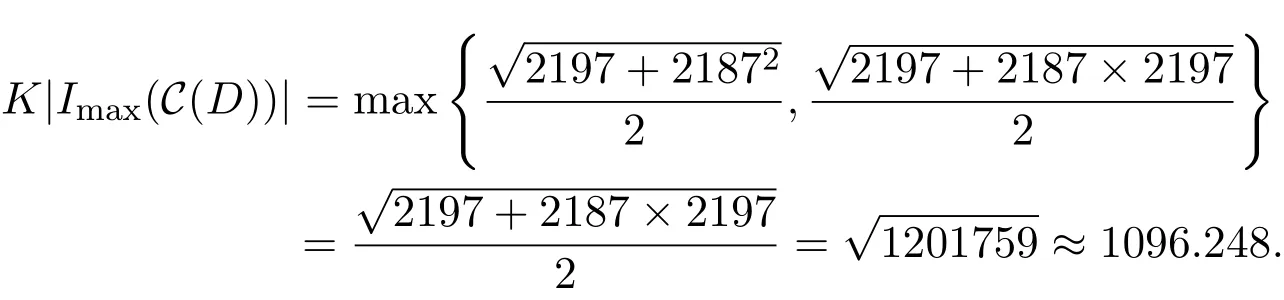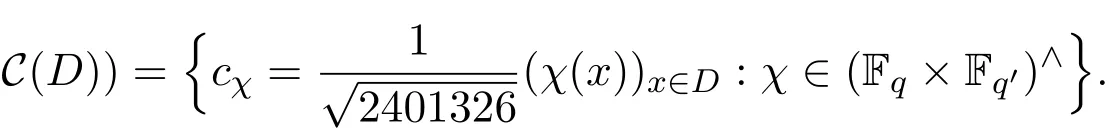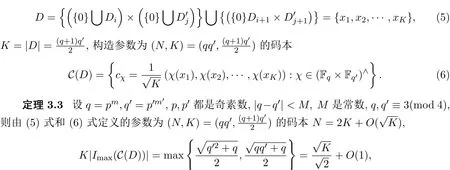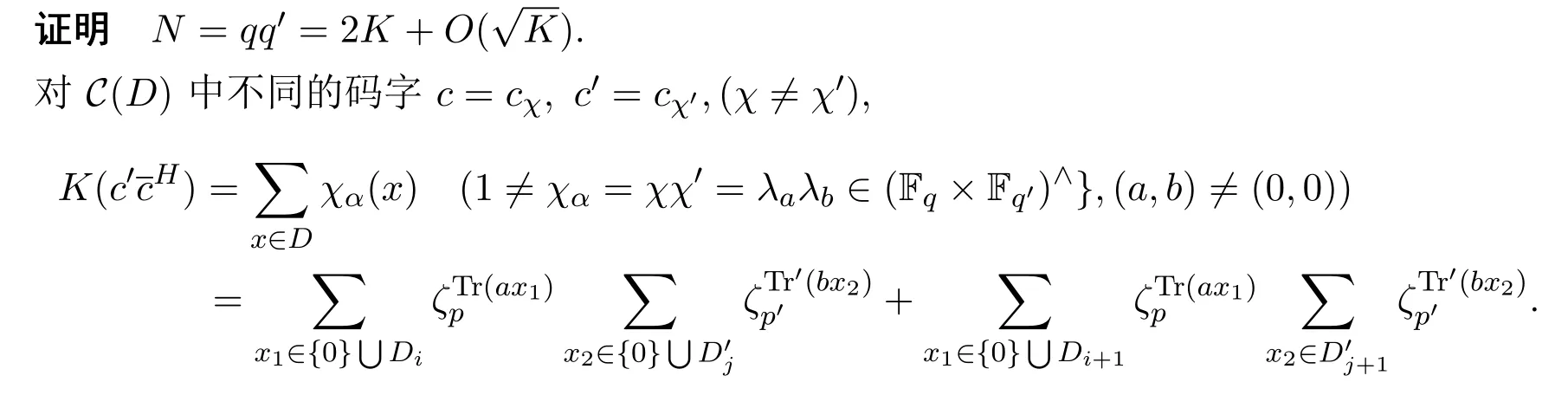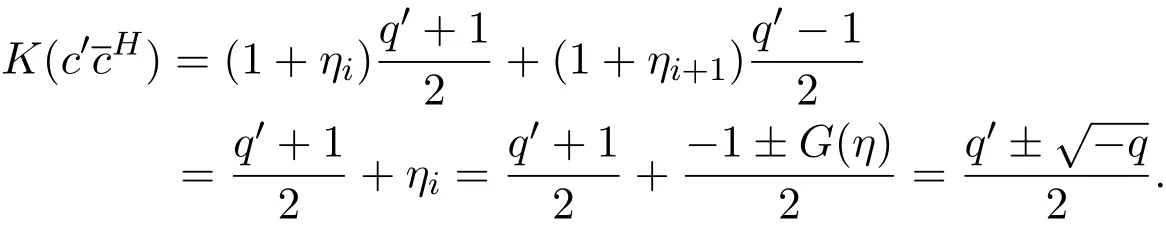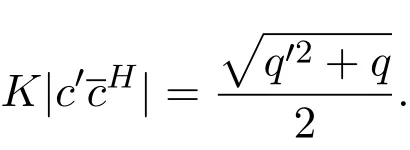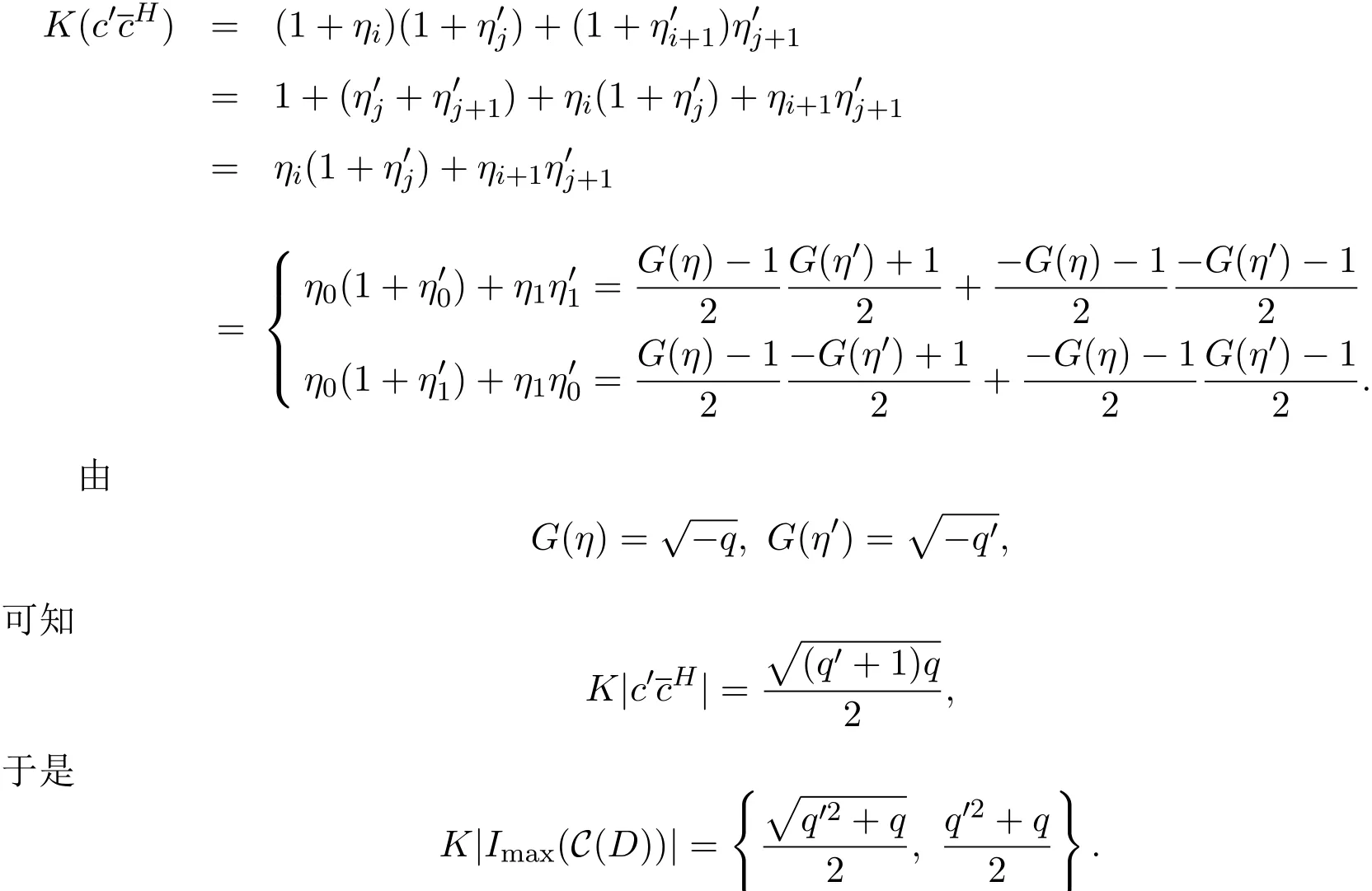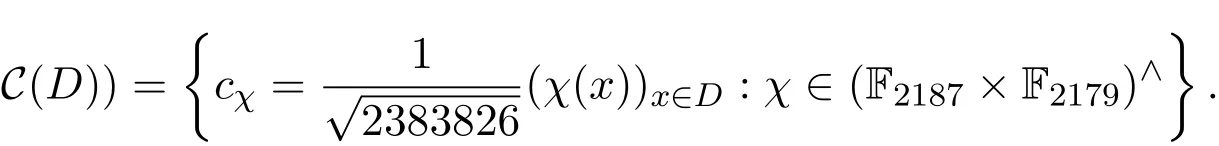幾類近似達到Welch界碼本的構(gòu)造
張愛仙,何春燕,吉喆
(西安理工大學(xué)數(shù)學(xué)系,陜西 西安 710048)
1 引言
設(shè) CK是 K 維復(fù)向量空間,u=(u1,u2,···,uK),v=(v1,v2,···,vK)∈ CK,定義 u,v的厄米特(Hermitian)內(nèi)積為

當(u,u)=1時,稱u是單位向量.
定義 1.1 設(shè)N>K,一個參數(shù)為(N,K)的碼本(codebook)C是指CK中N個單位向量構(gòu)成的集合 C={c1,c2,···,cN}.
當1≤i?=j≤N 時,ci和cj的互相關(guān)值定義為|(ci,cj)|.碼本C的最大值定義為
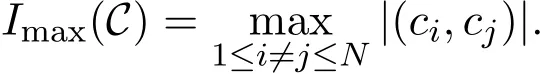
Imax(C)的值很小的碼本C,即具有低相關(guān)值的碼本C在分頻多址通信中有著重要的應(yīng)用,它們用來區(qū)分不同用戶發(fā)出的信號.近年來,碼本在量子通信,編碼理論,填充,密碼學(xué)中也有廣泛的應(yīng)用[1-4].
引理 1.1[5]對于參數(shù)(N,K)的碼本,有

這就是著名的Welch界,用Welch界來衡量碼本的好壞,達到Welch界的碼本,稱為是最佳的.但目前絕大多數(shù)最佳的碼本都是基于交換群上的差集合構(gòu)造的,構(gòu)造差集合是組合數(shù)學(xué)中的一個困難問題,并且由于差集合的參數(shù)(v,k,λ)之間要滿足k(k?1)=λ(v?1),所以有很多差集合不存在性的結(jié)果,也就是說很多參數(shù)的最佳碼本是不存在的.
2 預(yù)備知識
文獻[6]中作者考慮用幾乎差集合構(gòu)造近似最佳的碼本.下面給出近似最佳碼本的定義及本文中要用到的有限域上的分圓類,高斯和,高斯周期等概念和相關(guān)結(jié)果.
定義 2.1[7]一個參數(shù)為(Nn,Kn)的碼本系列Cn(n=1,2,···)叫作是近似最佳的,是指當n→∞時滿足以下兩個條件:
(1)存在常數(shù)c,0 (2)存在正常數(shù) c′,使得 引理 2.1[7]碼本系列C是近似最佳的是指如果存在常數(shù)c>1滿足以下兩個條件: 令 p是素數(shù),q=pm,Fq是 q個元素的有限域,=Fq{0}是 q?1階循環(huán)群.Tr:Fq?→Fp是有限域上如下定義的跡映射: 下面給出本文中將會用到的高斯和的幾個性質(zhì). 引理 2.2[8-9](1)當 χ=1(平凡特征),G(χ)=?1.當 χ?=1, 其中χ=χ?1是χ的共軛特征. (2)令q=pm,p≥3,χ是Fq的二次特征,則 是Fq上的e階分圓類.關(guān)于分圓類更詳細的性質(zhì),可參見文獻[10].Fq上的e階高斯周期定義為 高斯周期與高斯和有如下關(guān)系,設(shè)χ是Fq上的e次特征,χ(α)=ζe, 設(shè) q=pm,q′=p′m′,p,p′都是奇素數(shù).本節(jié)考慮群 Fq×Fq′上近似最佳碼本的構(gòu)造,其中q,q′→∞,|q?q′| 其中 Tr′:Fq′?→ Fp′是跡映射. 構(gòu)造 1 考慮加法群Fq×Fq′中如下子集合: 從而碼本C(D)近似達到Welch界,是近似最佳碼本. 對 C(D) 中不同的碼字 c=cχ,c′=cχ′,(χ ?= χ′), (1)當 a=0,b?=0 時, 其中η′是Fq′的2次高斯周期,由引理2.2及高斯和的正交性=?1可得上式.于是 (2)當 a ?=0,b=0 時, (3) 當 a ?=0,b ?=0 時, 例 3.1 取 Fq×Fq′=F2187×F2197=F37×F133,α,β分別是 Fq,Fq′的本原元,取子集合D為 構(gòu)造參數(shù)為(N,K)=(4804839,2401326)的碼本 由定理3.1可知, Welch界為 構(gòu)造 2 考慮加法群Fq×Fq′中如下子集合: 從而碼本C(D)近似達到Welch界,是近似最佳碼本. 證明 證明過程與定理3.1類似. 例 3.2 取Fq×Fq′=F1331×F1327=F113×F1327,1327是素數(shù),α,β 分別是F1331,F1327的本原元,取子集合D為: 構(gòu)造參數(shù)為(N,K)=(4804839,2401326)的碼本 由定理3.2可知, Welch界為: 注 3.1 文獻[11]中作者考慮了分圓類并兩個零元素和四個零元素的情形,下面討論分圓類并三個零元素作為子集合的情形. 構(gòu)造 3 考慮加法群Fq×Fq′中如下子集合 從而碼本C(D)近似達到Welch界,是近似最佳碼本. (1)當 a=0,b?=0 時, 其中η′是Fq′的2次高斯周期,由高斯和的正交性可知=?1. (2)當 a ?=0,b=0 時, 于是 (3) 當 a ?=0,b ?=0 時, 例 3.3 取 Fq×Fq′=F2187×F2179=F37×F2179,2179是素數(shù),α,β分別是 F2187,F2179的本原元,取子集合D為 構(gòu)造參數(shù)為(N,K)=(4765473,2383826)的碼本 由定理3.3可知, Welch界為: 從而碼本C(D)近似達到Welch界,是近似最佳碼本.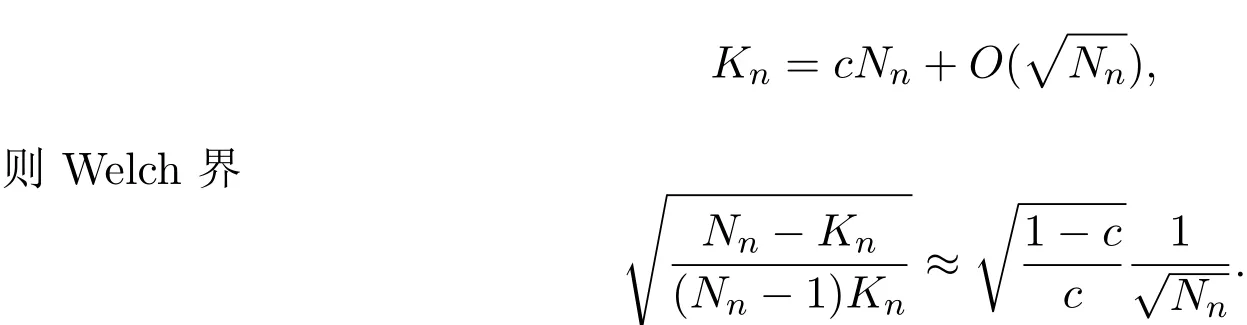
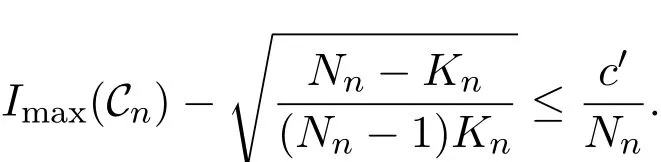
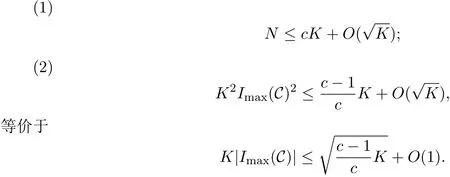
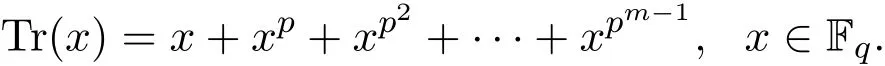
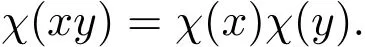
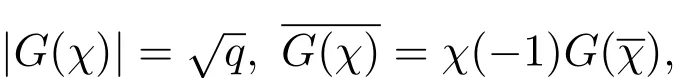
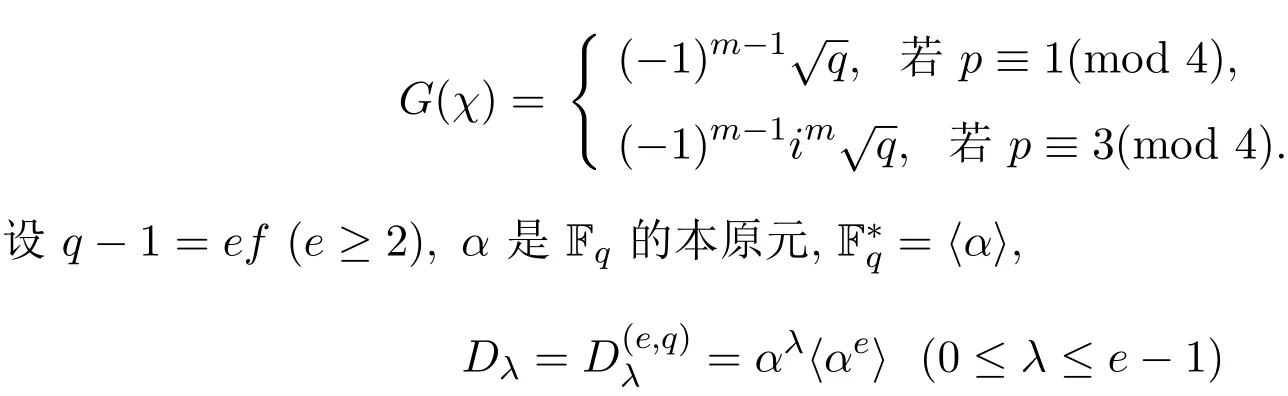
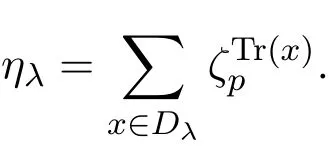
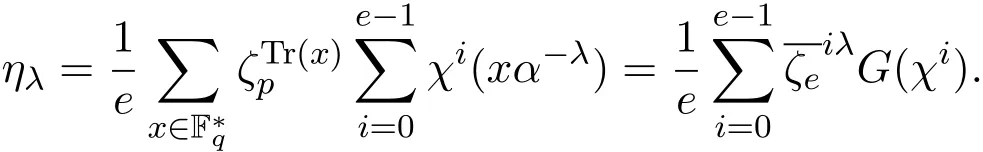
3 近似最佳碼本的構(gòu)造