LCLC補償型電場耦合式無線電能傳輸系統特性分析

余江華，孫巖洲，張笑林，韋延方

（河南理工大學 電氣工程與自動化學院，焦作 454000）

0 引言

無線電能傳輸（Wireless Power Transfer，WPT）技術是指不通過直接的電氣連接將電能從電源側傳輸到負載側的一種新型電能傳輸方式，可使用電設備擺脫傳統的線纜束縛，在一些特殊的場合有著美好的應用前景[1]。基于電場耦合式電能傳輸（Electrical-field coupled power transfer，ECPT）技術作為無線電能傳輸技術之一，采用金屬薄板作為發射電極和拾取電極，通過極板間建立的高頻電場作為載能介質，實現電能的無線傳輸，具有電磁干擾性小，耦合機構靈活性高的特點[2～5]。目前該技術已在植入式醫療器械和電動汽車等近距離傳輸場合得到應用[6,7]。由于ECPT系統中耦合機構的等效耦合電容值較小，耦合容抗大，需要對系統的耦合機構進行諧振補償[8]，目前ECPT技術多采用LC串聯諧振補償網絡[9]，采用該種補償方式存在補償電感體積過大以及系統對諧振頻率的魯棒性較差等問題。

文獻[10,11]將LCLC補償網絡運用到ECPT系統中，在有效解決上述問題的同時也使ECPT系統的傳輸功率和效率產生了質的飛躍[12]。經研究發現，由于該補償網絡階數較高，參數變化時對系統輸出功率和效率有著較大的影響，然而對于一個ECPT系統來說，相關參數特別是耦合電容、負載和諧振頻率等具有較大的變化特性。為了得到雙邊LCLC對稱補償型ECPT系統中易變參數對系統輸出特性的影響規律。本文通過電路理論建立LCLC對稱補償型ECPT系統的等效電路模型，分析了耦合機構的等效電容、旁路并聯電容、負載和頻率變化時對系統輸出功率和效率的影響規律，所得結果可為LCLC對稱諧振型ECPT系統的設計和調試提供參考。

1 系統建模

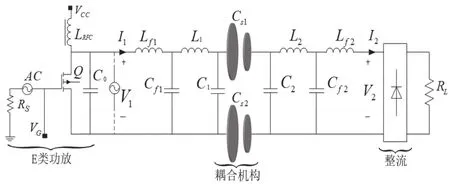
圖1 系統等效拓撲電路圖

所設計的完整ECPT系統電路如圖1所示，采用E類功率放大器作為系統的高頻電源；耦合機構作為ECPT系統的核心部件，由兩對銅制薄板構成；為減小系統的諧振補償電感量，發射極板側和接收極板側并聯旁路電容C1和C2；由于本文主要分析LCLC對稱諧振型補償網絡，為簡化分析電路，將E類功放等效為輸入電壓源V1，負載側獲取電壓等效為V2；耦合機構等效為集總電容CS1和CS2。

在理想情況下耦合機構等效集總電容CS1和CS2的表達式為：

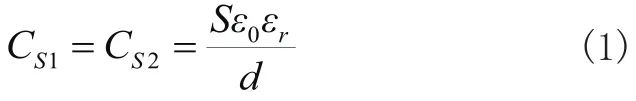
式中S為耦合極板有效耦合面積，d為耦合間距，（8.85×10-12）為真空介電常數，為所選電介質的相對介電常數。

系統兩邊采用對稱式結構設計，對應位置上元器件參數取值相等，即Lf1=Lf2、Cf1=Cf2、L1=L2、C1=C2；等效耦合電容CS1、CS2串聯成總耦合電容CS，CS與C2串聯后再與C1相并聯為電容Ch；Lf1和Cf1在角頻率ω下發生諧振；L1與Ch發生諧振的同時也要與Cf1發生諧振；各元器件相互關系表達式[10,11]為：

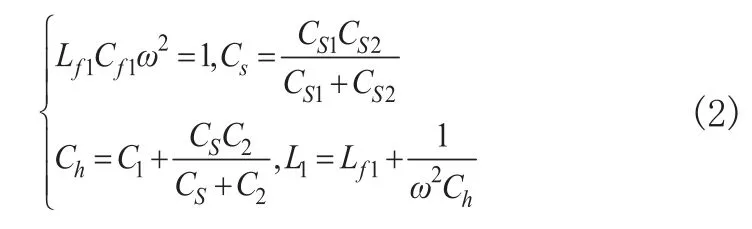
等效電源V1與I2關系表達式，等效負載電壓V2與I1的關系表達式以及輸出功率的表達式為：

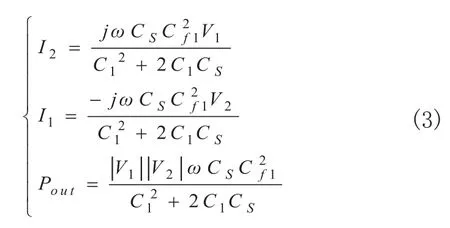
根據電路理論可知±j可以看成旋轉因子，即輸出電流I2超前輸入電壓V190度，輸入電流I1滯后輸出電壓V290度，輸入側電壓電流同相位，輸出側電壓電流同相位，且與負載性質無關。

由于系統的補償網絡階數較高，為進一步簡化分析電路，應用電路星三角聯結等效變換理論將圖1轉化為圖2所示的等效電路圖。

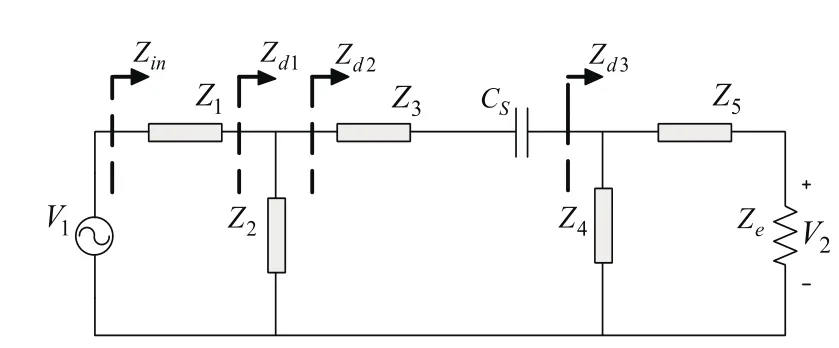
圖2 星三角變換等效電路

系統采用對稱式設計，對應位置上元件參數取值相等，經過星三角理論變換后對應位置上等效阻抗依然相等，即Z1=Z5、Z2=Z4，等效阻抗表達式為：

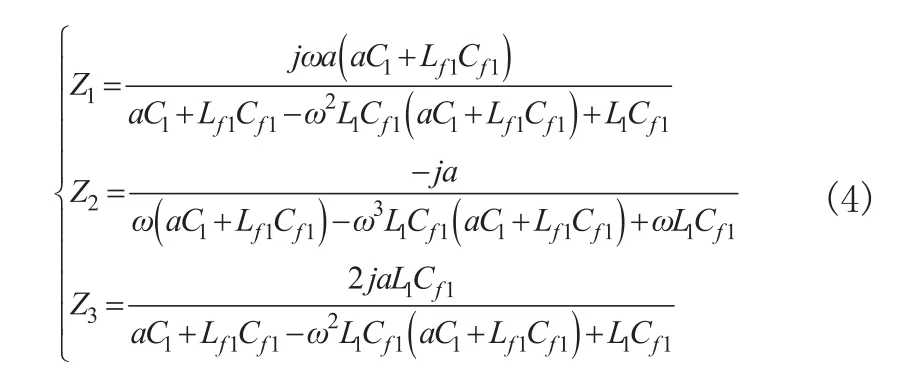
式中a=Lf1+L1-ω2Lf1L1Cf1。

各級等效阻抗表達式Zd1、Zd2、Zd3的表達式為：

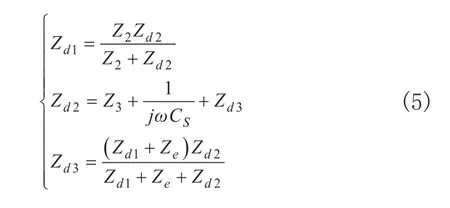
采用阻抗變換原理建立等效電路圖2的電壓增益模型為：

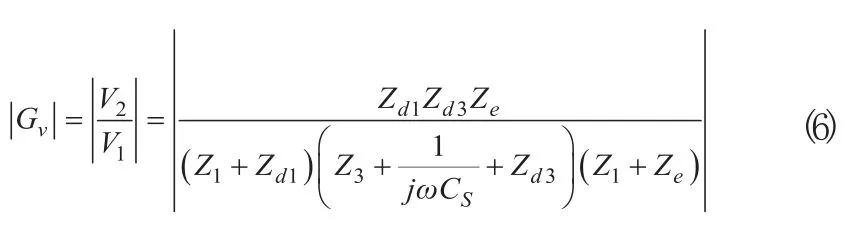
將式(4)、式(5)代入式(6)可得關于參數Z1、Z2、Z3、Ze、ω、CS的電壓增益表達：

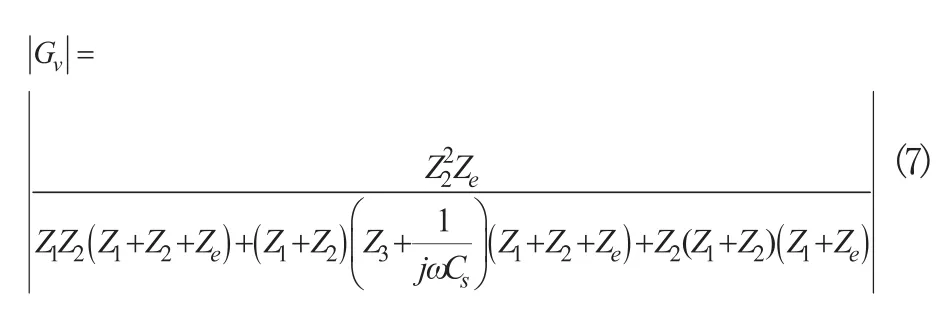
圖2中系統輸入阻抗Zin的表達式為：

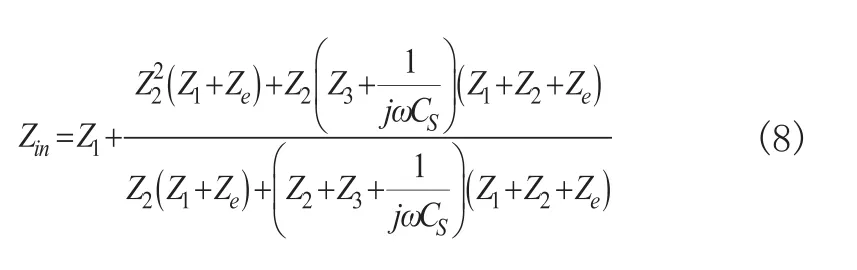
系統輸出功率和效率的表達式為：

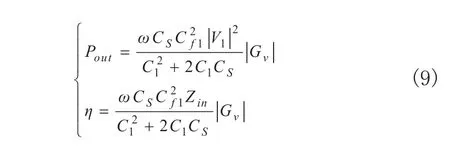
式中|Gv|和Zin取值如(7)、式(8)所示。

2 系統傳輸特性分析

本文設計的系統模型傳輸功率30W，負載50Ω，電源和負載側電壓幅值均取值55V，耦合機構等效電容200pF，旁路并聯電容設定為500pF，系統頻率設定為13.56MHz。通過式(2)和式(3)可計算系統其他元件參數，具體參數取值如表1所示。

表1 系統參數及元件值

以表1參數為基礎，通過MATLAB仿真分析系統的頻率f、等效耦合電容CS、旁路電容C1和負載Ze變化時對系統輸出功率Pout和效率η的影響規律。

2.1 輸出功率、效率隨頻率的變化規律

其他參數為設計值時，改變系統的頻率，得到系統輸出功率和效率隨頻率的變化規律如圖3所示。

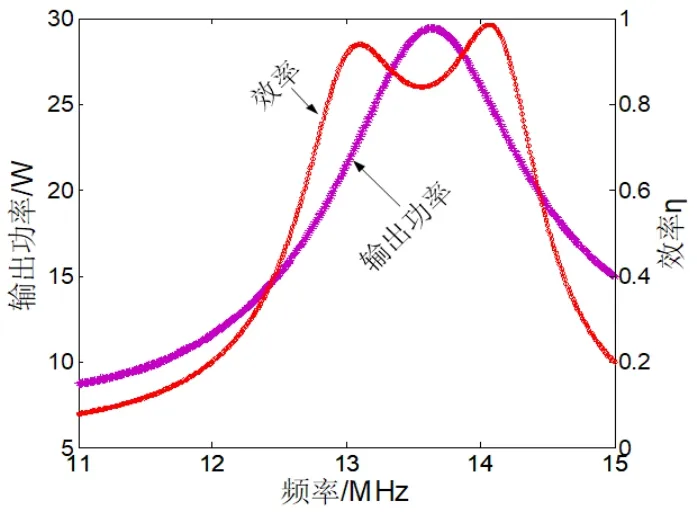
圖3 輸出功率、效率隨頻率的變化規律

由圖3可知輸出功率隨著頻率的增大先增大后減小，在諧振點達到最大值，頻率的減小相對于頻率的增加對輸出功率的影響更為顯著；系統效率在諧振頻率點的兩側取得最大值，LCLC對稱補償型ECPT系統存在頻率分裂現象，在調試過程中，可適當的增加或降低系統頻率，以獲取最優的系統傳輸效率。

2.2 輸出功率、效率隨等效耦合電容和旁路并聯電容的變化規律

在實際應用中，ECPT系統的耦合極板很難保證精確對位，相對位置易發生變化，使兩對耦合極板之間發生交叉耦合，在引起耦合機構等效電容變化的同時，也會造成旁路并聯電容值發生改變。

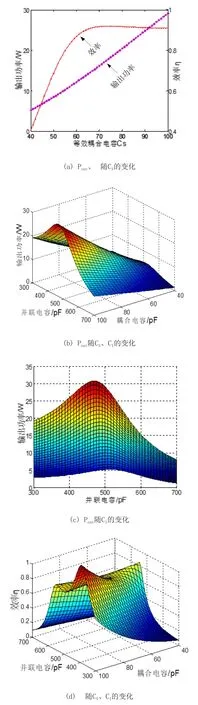
圖4 Pout、η隨C1、CS的變化規律

由圖4(a)可知隨著耦合機構的等效電容減小系統輸出功率減小。系統效率在等效耦合電容值減小到設計值的60%時才開始大幅下降，即系統效率對等效耦合電容的變化具有較高的魯棒性；由圖4(b)可知當等效耦合電容值降低時，交叉耦合引起的旁路并聯電容增大會進一步降低系統的輸出功率；通過視角改變法可由圖4(b)得到圖4(c)，由圖4(c)可知當旁路并聯電容減小時，系統輸出功率先增大后減小且可取到最大值；由圖4(d)可知系統的旁路并聯電容大于或小于設計值時，系統效率均先增大后再減小且都可取得最大值；綜合圖4(c)和圖4(d)可知，當旁路并聯電容減小時，系統的輸出功率和效率都可取得最大值，即在系統的設計和調試過程中可在理論值的基礎上適當的減小旁路并聯電容的值，不僅有利于減小交叉耦合帶來的影響，也可使系統的輸出功率和效率均達到最優。

2.3 輸出功率、效率隨負載的變化規律

其他參取值為系統的設計值，系統的負載Ze分別取值為R，RL，RC。圖5示出三種負載變化時對系統輸出功率和效率的影響規律。

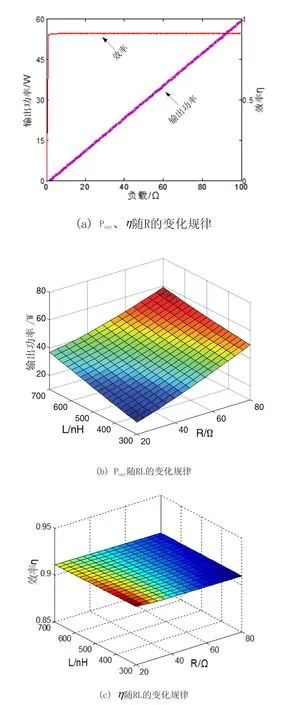
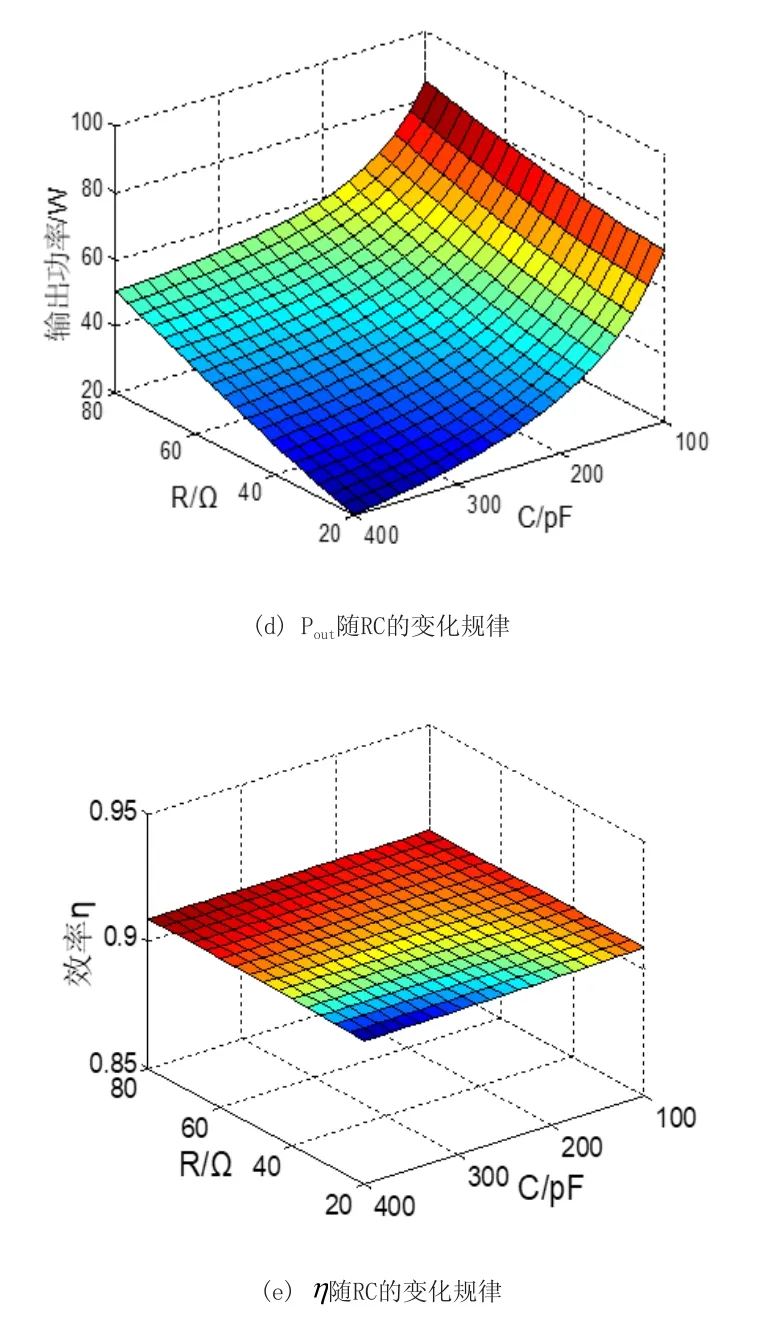
圖5 輸出功率和效率隨負載的變化規律

由圖5(a)、圖5(b)和圖5(d)可知系統的負載呈阻性、感性或容性時，系統的輸出功率均隨著負載的等效阻抗增大而增大；由圖5(a)、圖5(c)和圖5(e)可知系統的輸出效率不隨負載的變化而變化，系統對負載的變化具有較高的穩定性。

3 實驗

為驗證上述系統的輸出特性，搭建如圖6(a)所示的實驗電路，并省略整流模塊。采用高頻高效的E類功率放大器為系統提供高頻電能，能夠實現輸出功率30W，帶寬2MHz；采用4塊半徑為49mm的銅板作為耦合極板，可獲得最大耦合電容200pF。實驗參數在系統設計參數（表1）的基礎上根據分析所得的輸出功率最優原則選擇頻率13.56MHz，等效耦合電容為200pF，旁路并聯電容C1(C2)為450pF，負載為50Ω，測得在輸出功率最優原則下負載側的電壓幅值為50.4V，如圖6(b)所示。

因實驗條件有限，通過測量負載側獲取的電壓幅值估算輸出功率的變化趨勢。當負載分別取值25Ω、50Ω和75Ω時測得負載側電壓幅值隨頻率和等效耦合電容的變化規律如圖7所示，由圖7(a)可知隨著頻率的增大，系統取3種負載時輸出電壓幅值均先增大后減小，基本都在諧振頻率點達到最大輸出電壓。在同一頻率下，負載等效阻抗越大，輸出電壓幅值越高。由圖7(b)可知，在三種負載下系統的輸出電壓幅值隨著等效耦合電容量的減小而減小，與圖4仿真獲得的變化趨勢基本一致。

圖6 ECPT實驗電路及最佳參數時電壓波形

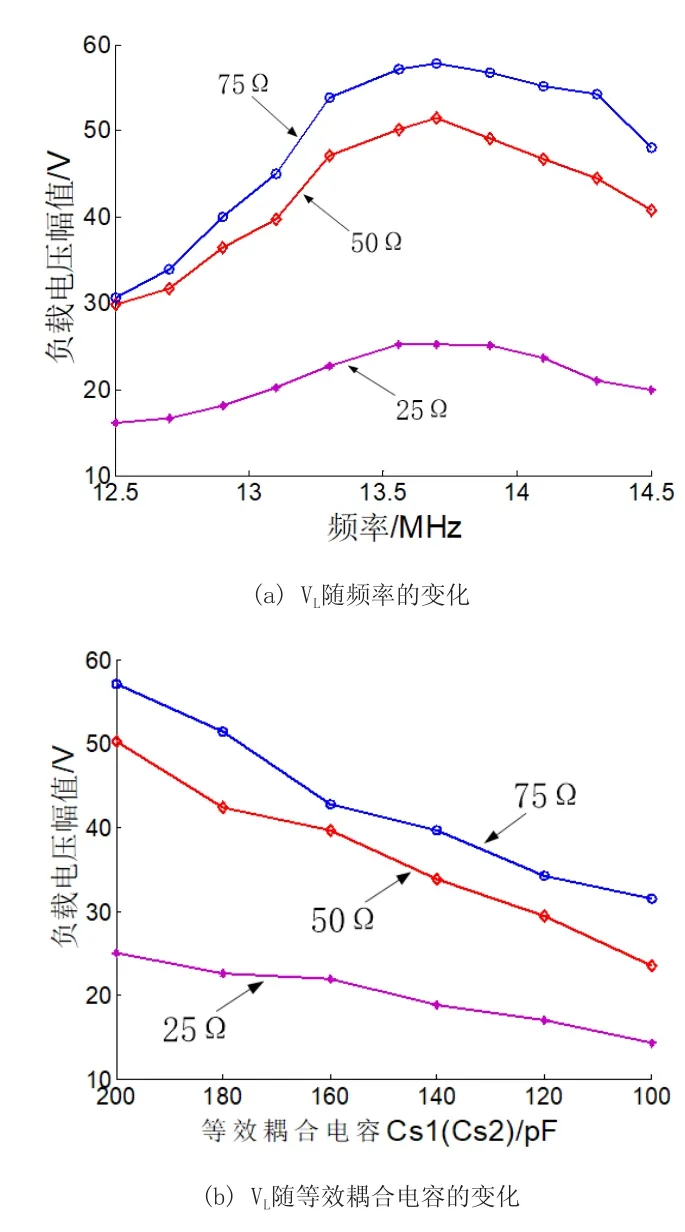
圖7 VL隨頻率和等效耦合電容的變化規律

4 結束語

針對雙邊LCLC對稱補償型ECPT系統的輸出特性易受影響，而在實際應用中耦合機構的等效電容、旁路電容、負載和頻率等參數又易發生變化的問題。通過電路理論建立系統的等效電路模型，采用MATLAB仿真分析系統的傳輸功率和效率與系統的等效串聯電容、旁路并聯電容、負載和系統頻率的變化規律。結果表明，由于存在頻率分裂現象，系統在設計諧振頻率值的兩側達到最優輸出效率。當等效耦合電容的變化范圍小于系統設計值的40%時，系統可保持較高的輸出效率。旁路并聯電容小于設計值時，不僅有利于減小交叉耦合帶來的影響，也可使系統的輸出功率和效率均達到最優。系統的輸出功率隨負載的等效阻抗增加而增加，系統效率不隨負載變化而變化。在LCLC對稱補償型ECPT系統的設計和調試過程中可綜合調整系統頻率、耦合電容、并聯電容、負載使系統的輸出功率和效率取得最佳。