一種線性電路狀態空間模型的提取方法
丁家峰,梁 健,李新梅,丁一鵬,趙 巖
(中南大學 物理與電子學院,長沙 410012)
0 引言
電路的動態分析是電路分析的重要組成部分,是了解電路系統動態復雜行為的重要手段。對電路進行動態分析,常常使用節點分析法和狀態變量法。節點分析法是早期用于處理電路直流分析而建立起來的方法,后來經過發展常被用于電路的動態分析中[1]。使用節點分析法對電路進行動態分析時,一般使用數值積分法將儲能元件如電容、電感等效為電流源與電阻的并聯或串聯,從而在每一個時刻點將電路等效為電阻網絡進行求解[2,3]。由于無法得到任意時刻的電路狀態,近年來,對節點分析法研究僅限于如何加速求解過程,很少涉及電路理論本身[4]。
狀態變量法是分析電路的有力工具,其最早應用于控制系統分析,后來被廣泛運用到電路網絡的動態分析中。狀態變量法對系統進行分析的關鍵是提取出系統的狀態方程。狀態方程是用一組狀態變量和輸入信號共同描述的微分方程組。狀態變量一般是系統內部的量,在線性網絡中,一般選取電容電壓和電感電流作為系統狀態變量[5]。使用狀態變量法分析電路,相比其他的分析方法,具有如下優點:1)無論是線性電路還是非線性電路,只要找出合適的狀態變量,都可以使用狀態變量法進行分析[6];2)只要得到電路在某個時刻t0的一組狀態變量,就可根據狀態方程得出任一時刻t(t>t0)的電路狀態;3)使用狀態變量法對電路進行分析,最終都會得到一組一階微分方程,其十分便于利用計算機進行求解。因此,狀態變量法常常被用于系統的建模和分析中[7]。但是系統狀態方程的提取不是一個簡單的問題,傳統的以電容電壓和電感電流作為狀態變量的提取方法一般通過復雜的網絡分析得到標準形式的狀態方程,其過程包含了復雜的網絡圖論理論[8]。這種方法列寫狀態方程十分復雜,有時甚至不能得到標準形式的狀態方程。為了使用狀態變量法分析電路方便研究工作,人們提出了一些非標準形式的狀態空間模型[9,10],最常用的就是基于系統傳遞函數的狀態空間模型。根據系統傳遞函數提取系統狀態方程的問題被稱為傳遞函數的實現問題。如果選取的狀態變量不同,根據傳遞函數可以得到不同的狀態方程。每個狀態方程被稱為傳遞函數的一個實現,其中能控規范形和能觀規范形是最基本的兩種實現[11]。這類狀態方程與標準的狀態方程的不同之處在于其不能保證選取的狀態變量為電容電壓或者電感電流,甚至有可能是一個不存在物理意義的量。但這類狀態方程十分便于對系統進行描述與分析,特別是在控制系統理論中運用十分廣泛,一般可以根據這類狀態方程去構造真實的物理系統,對其提取方法進行研究是一件十分有意義的事情[12]。要想獲得這類狀態方程,就必須先得到系統的傳遞函數。對于簡單的電路和系統,其傳遞函數可以通過計算直接得到,但復雜電路和系統的傳遞函數較難求取,往往只能通過實驗或者擬合的方式得出,這給狀態方程的提取帶來了困難。
為了解決復雜電路和系統求取傳遞函數中存在的困難,方便得到傳遞函數的狀態空間實現,本文提出了一種適用于線性電路的狀態空間模型提取方法。該方法將電路復頻域分析方法和改進節點法相結合,使用符號運算求解出線性系統的傳遞函數,通過傳遞函數提取出單輸入——單輸出系統的能控規范形和能觀規范形兩種基本實現。
1 線性系統的狀態空間描述
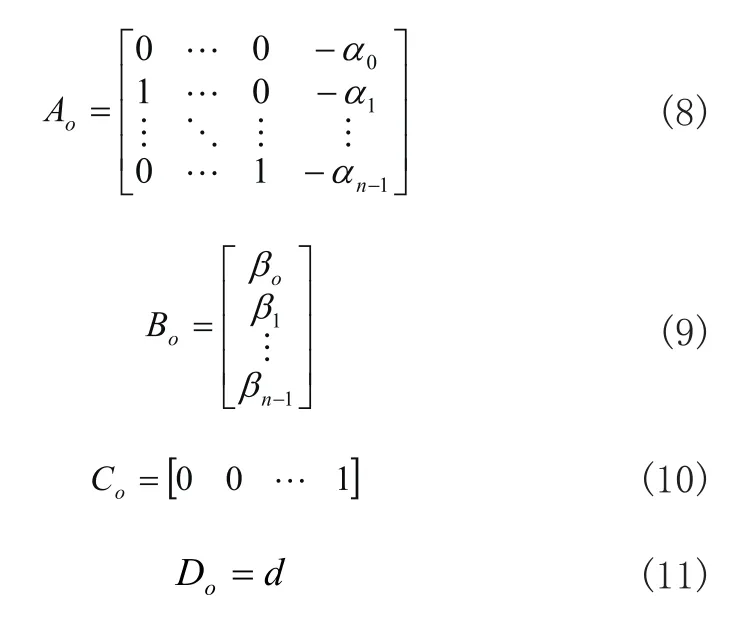
單輸入——單輸出系統的狀態空間描述可表示為:
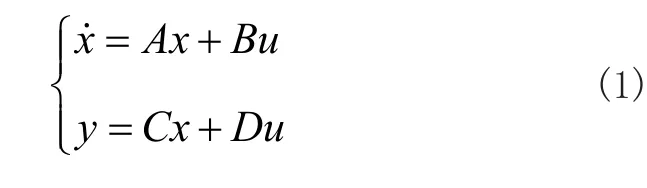
其中,x為狀態變量,u為系統輸入,y為系統輸出,A為系統矩陣,B為輸入矩陣,C為輸出矩陣,D為耦合矩陣。在傳遞函數的多種狀態空間實現中,能觀規范形實現和能控規范形實現為最基本的兩種實現方式。
考慮物理可實現的單輸入——單輸出系統的傳遞函數:
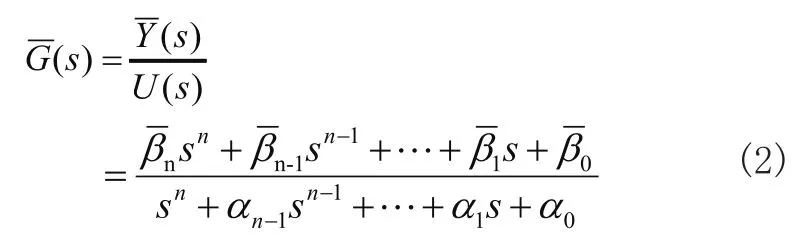
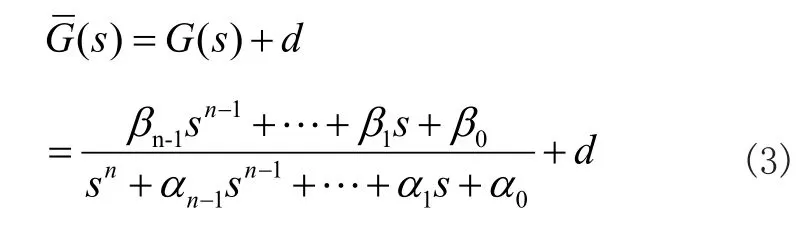
其中,G(s)為嚴真情形,d為直接輸入分量。根據傳遞函數,可得出單輸入——單輸出系統的能控規范形的系數矩陣為:
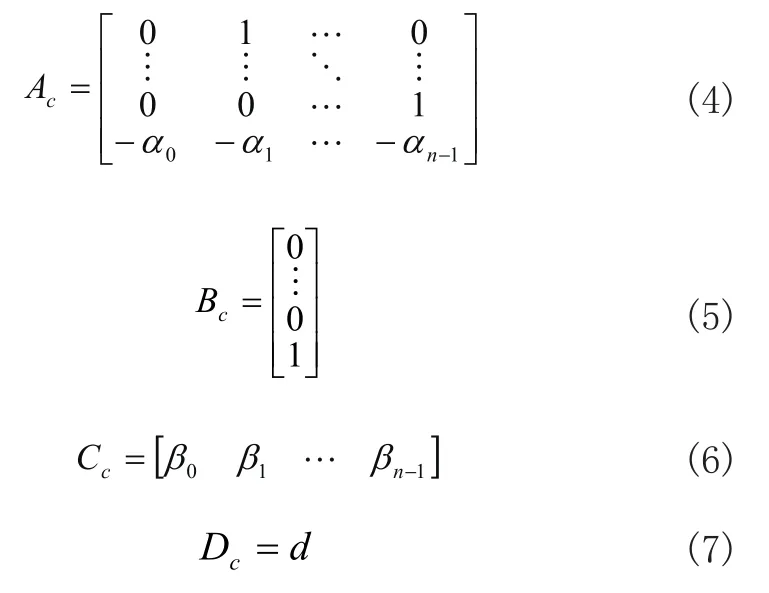
單輸入——單輸出系統的能觀規范形的系數矩陣為:
2 算法分析與設計
觀察系統規范形實現的系數矩陣可知,如果已取得系統的傳遞函數,可將傳遞函數變換出嚴真情形,提取出分子和分母多項式的系數,根據這些系數便可構成系統規范形實現的系數矩陣。因此,如何提取系統狀態方程的問題可以轉變為如何求取系統傳遞函數的問題。根據傳遞函數,我們用算法實現了單輸入——單輸出系統的能控規范形實現和能觀規范形實現這兩種基本狀態空間模型的提取,其算法流程圖如圖1所示。
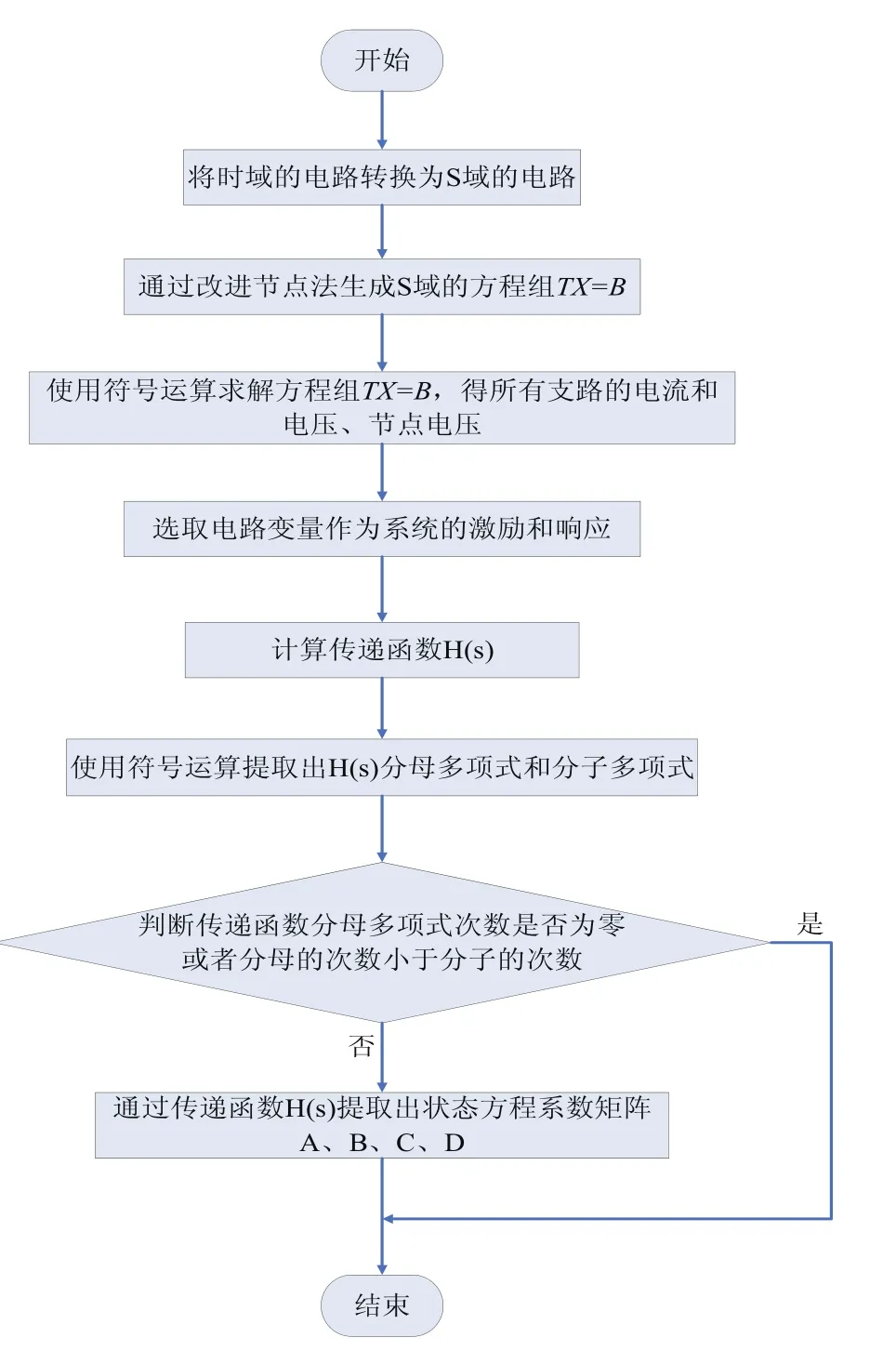
圖1 算法流程圖
2.1 基于線性電路復頻域方法的電路元件參數分析
在電路分析領域,通常把系統輸入稱為激勵,記作f(t),把系統輸出稱為響應,記作y(t),系統傳遞函數可以表示為:

其中Y(s)和F(s)分別為零狀態下y(t)和f(t)的拉普拉斯變換。根據式(12)可知,要想得出系統的傳遞函數,必須先求出系統激勵和響應的拉普拉斯變換。本文使用線性電路復頻域分析的方法求出電路網絡激勵與響應的拉普拉斯變換。
在線性電路復頻域分析中,常常使用元件的S域模型,將時域的電路轉換為S域的電路;再根據基爾霍夫定律對S域電路列線性方程組進行求解,便可得到各個電路變量的拉普拉斯變換。由于拉普拉斯變換的線性性質,基爾霍夫定律在S域下的形式和時域下的形式相似,可以簡單表示為:對于任一節點,對任一回路,。根據元件的電壓與電流的時域關系和拉普拉斯變換的性質,可以得出各個元件的S域電路模型。
對于電阻元件,其電壓電流的時域關系為u(t)=Ri(t),兩邊取拉普拉斯變換,可得到電阻元件的S域關系形式為U(s)=RI(s)。因此,電阻的S域電路模型如圖2所示。
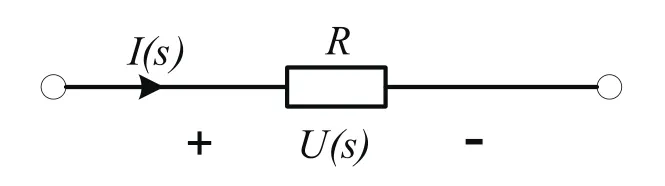
圖2 電阻S域電路模型
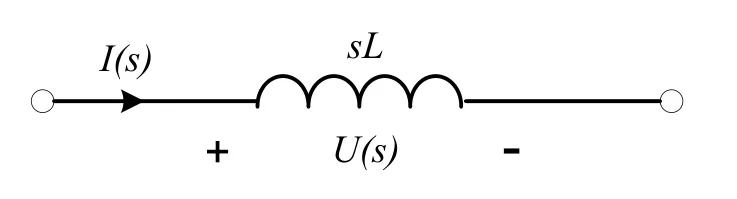
圖3 電感S域電路模型
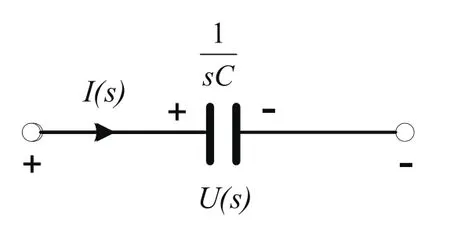
圖4 電容S域電路模型
對于電源元件,S域下的關系式為時域下關系式的拉普拉斯變換。其他的線性元件也可以根據拉普拉斯變換的性質得到S域的電路模型。
由上述可知,在時域中,電感及電容的電壓與電流之間的微分關系,在S域中變成了線性關系。因此,時域中的電路微分方程組,在S域中變成線性代數方程組,求解這個方程組,可以得到電路中有關電流和電壓的拉普拉斯變換,再根據激勵和選取的響應(已求得)的拉普拉斯變換,按式(12)求得響應與激勵之間的傳遞函數。那么,使用怎樣的方法在計算機環境下生成S域電路線性代數方程組?本文采用的是改進節點法。
2.2 基于改進節點法的電路網絡矩陣生成
改進節點法是常用的建立電路代數方程組的方法,其具有方便、快速等優點。許多仿真軟件如Spice使用了改進節點法建立代數方程組。
改進節點法的基本思想是將元件分為了三類。第一類是可用復電導描述的元件,包括電阻、電感和電容,它們的復電導分別為1/R、1/sL和sC;第二類是不能使用復電導描述的元件,主要包括獨立電流源和各種受控源;第三類元件為獨立電壓源。改進節點法根據三類不同元件對生成的代數方程組的貢獻,將元件貢獻填入代數方程組中,最終生成代數方程組TX=B。在這一過程中,第一類元件應最先被處理,這類元件的貢獻是構建出最基本的系數矩陣T,此時解向量X為節點電壓。第二類元件和第三類元件的處理順序可以任意選擇,其中獨立電流源主要對右端向量B有貢獻,各類受控源和獨立電壓源對系數矩陣T、右端向量B以及解向量X皆有貢獻[13]。
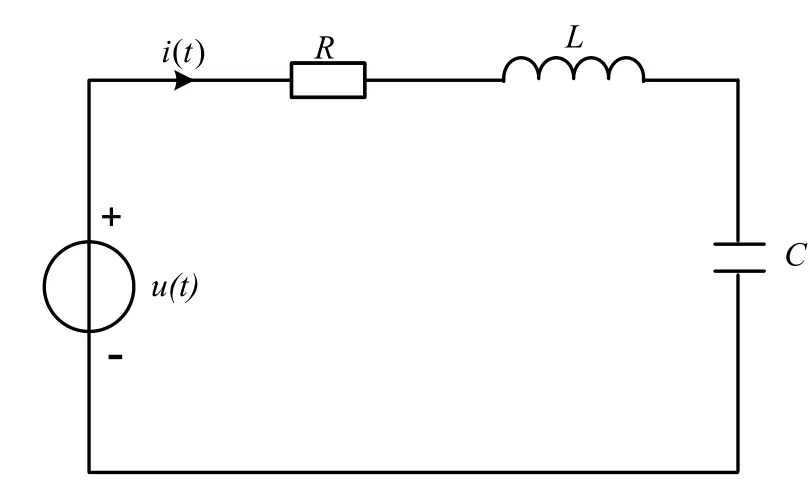
圖5 時域電路圖
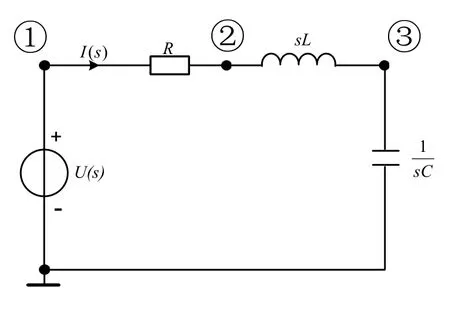
圖6 S域電路圖
RLC時域電路以及其在S域下的電路模型分別如圖5和圖6所示。使用改進節點法處理圖6電路生成的代數方程組TX=B為:
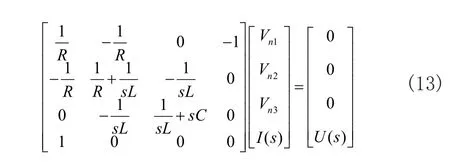
其中,Vn1、Vn2、Vn3為節點電壓,I(s)為流出電壓源的電流,s為拉普拉斯變換符號。由于生成的代數方程組中,含有符號變量s,所以需要使用具有符號運算功能的工具進行求解。
2.3 代數方程組的求解與狀態方程的提取
使用改進節點法生成代數方程組TX=B后,應使用具有符號運算功能的工具求解代數方程組。本文在MATLAB平臺上對算法進行了實現,MATLAB具有強大符號運算功能。當將代數方程組TX=B求解完成后,解向量X為節點電壓和非第一類元件支路電流的拉普拉斯變換表達式。由使用者確定電路系統激勵和響應,根據已求出的解向量,求出系統激勵和響應的拉普拉斯變換表達式,再根據式(12)求出單輸入——單輸出系統的傳遞函數。
假設得到的系統傳遞函數為:
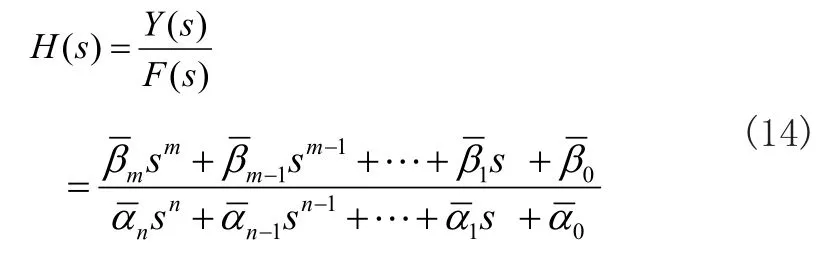
使用符號運算,分別將傳遞函數分子多項式Y(s)、分母多項式F(s)的系數向量提取出來,其中有:
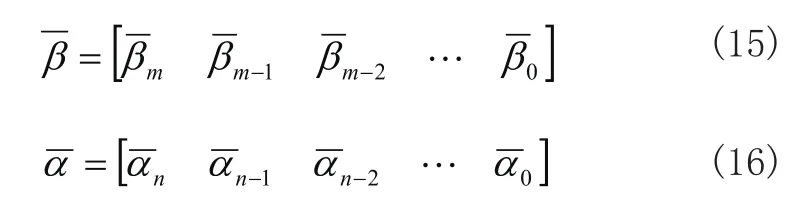

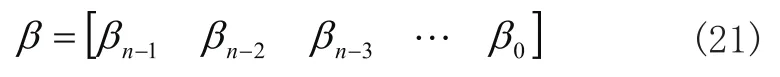
因此:
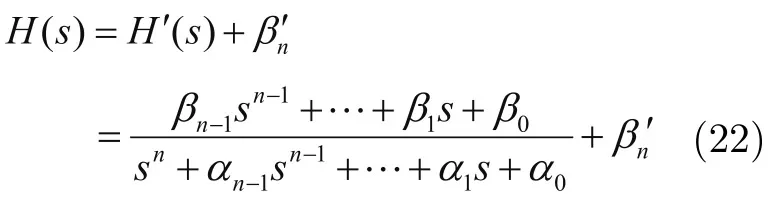
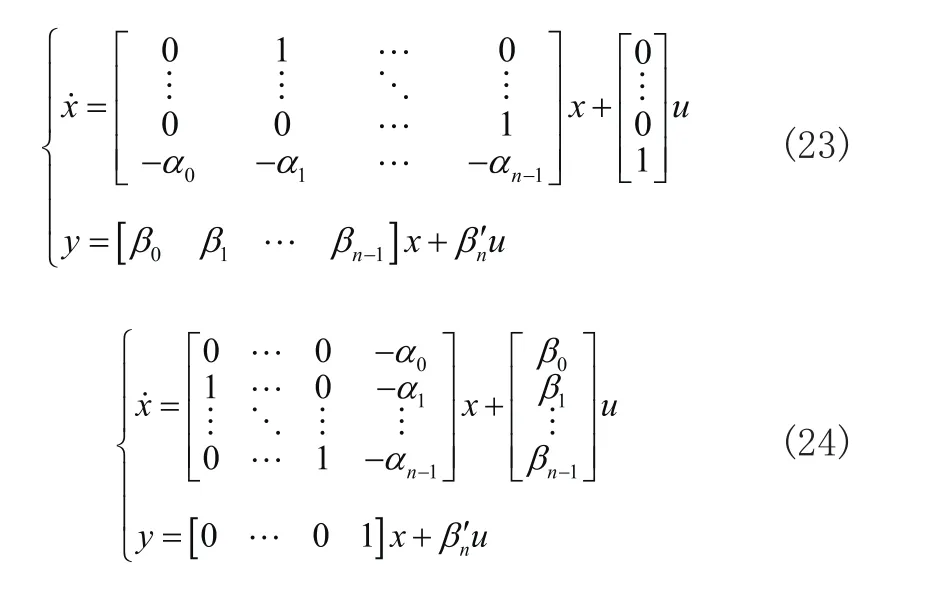
3 算例與分析
本文使用上述方法在MATLAB平臺上實現了狀態空間模型提取系統。圖7為提取系統的運行界面,該系統采用固定格式的描述文件對電路網絡進行描述。圖8為提取系統的運行流程圖,該系統讀取電路網絡描述文件進行分析,求解出系統傳遞函數,通過傳遞函數提取出電路系統的能控規范形實現和能觀規范形實現的系數矩陣。下面通過算例來說明如何使用該系統提取出狀態空間模型。
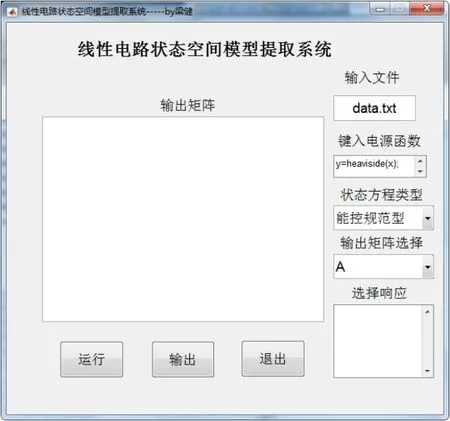
圖7 系統運行界面
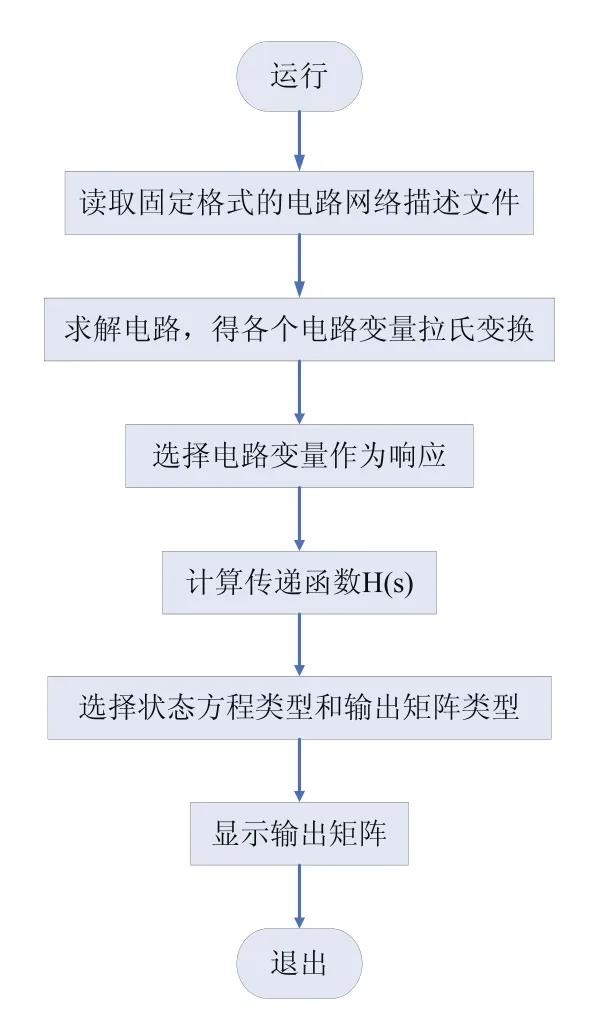
圖8 提取系統運行流程
圖9所示的算例電路較為復雜,元件E、H和G分別表示受控源VCVS、CCVS和VCCS,其傳遞函數較難直接求取,從而影響了狀態空間模型的生成。電路中包含著受控源、純電容回路和純電感割集,使用傳統的圖論提取方法較難提出狀態方程[5]。使用提取系統對圖9電路進行分析,填入電路拓撲描述文件和電源函數,點擊“運行”按鈕,便可生成代數方程組TX=B。使用符號運算求解代數方程組,得到所有節點電壓、支路電壓和支路電流的拉氏變換。
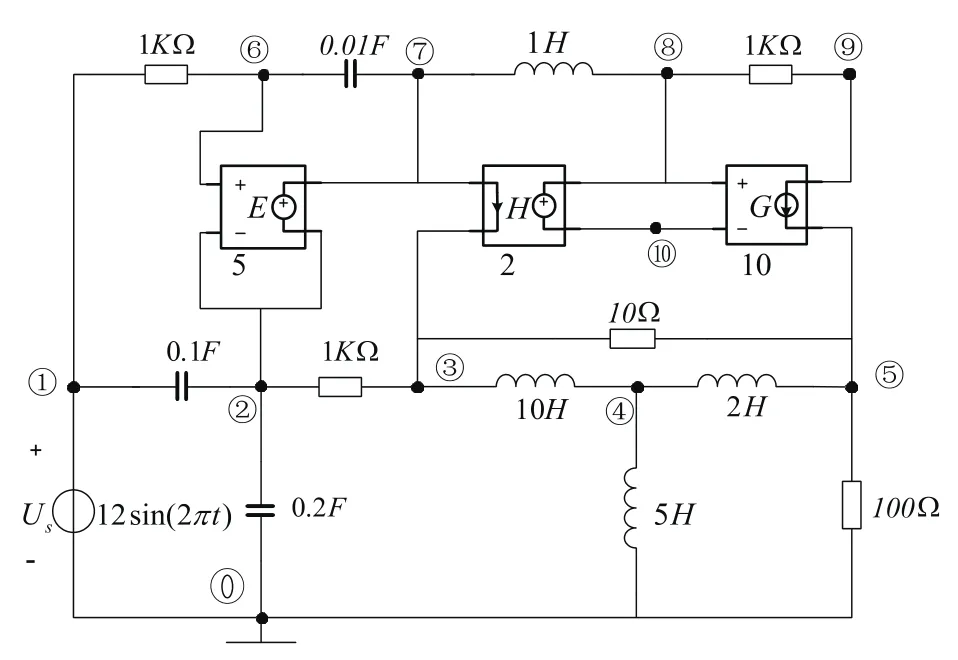
圖9 算例電路(電源頻率1Hz)
選取電壓源電壓作為激勵,節點5的電壓作為響應。節點5電壓的拉氏變換為:
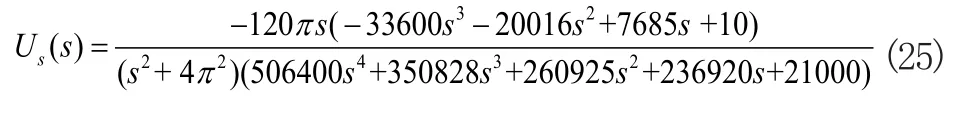
對式(25)進行反拉普拉斯變換,可得到節點5點電壓時域函數的近似表示為:
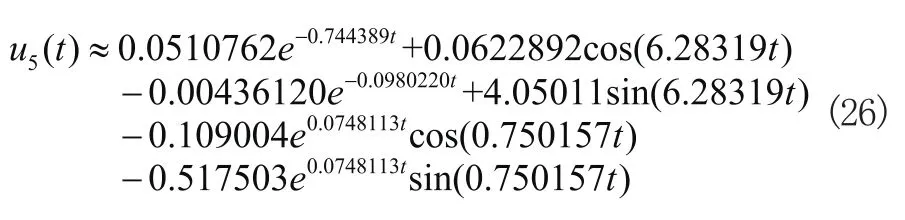
根據式(26)所繪出節點5電壓波形和使用Pspice軟件對電路進行仿真的結果的對比如圖10所示,其中Pspice在仿真過程中的最大步長為5ms。圖中的誤差曲線為,可以看出兩條曲線基本一致,誤差Δ保持在6×10-5以內,充分表明了所得到節點5電壓的拉普拉斯變換表達式是正確無誤的。
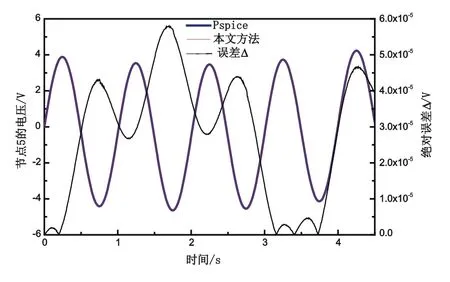
圖10 節點5電壓計算結果
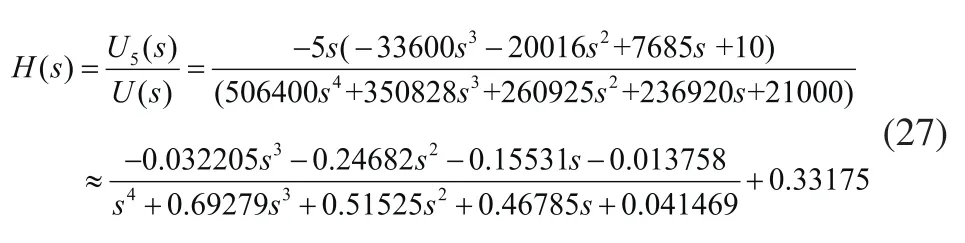
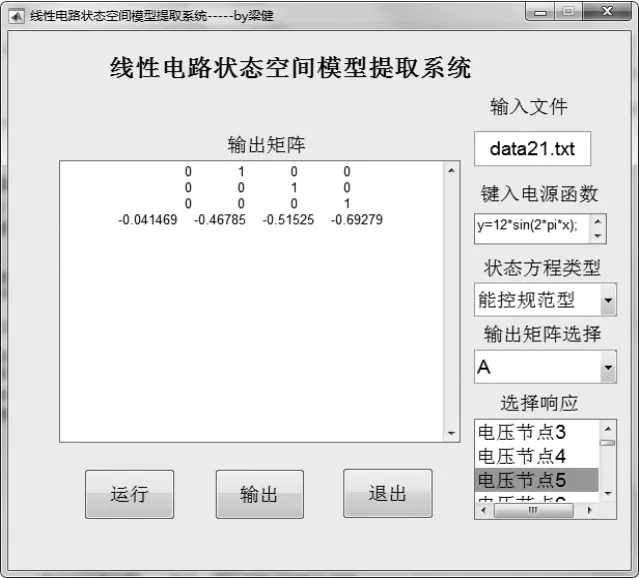
圖11 算例運行結果
根據傳遞函數和系統規范型實現的關系,由式(27)可得系統的能控規范型實現和能觀規范型實現分別如式(28)和式(29)所示。在提取系統上,選擇電壓節點5作為響應,點擊“輸出”按鈕,可得到算例運行結果如圖11所示。圖11中的輸出矩陣為能控規范形實現的系數矩陣A。通過將式(28)的系數矩陣A與圖11中的輸出矩陣對比可知,提取系統的運行結果是準確可靠的。

4 結束語
本文提出了一種適用于線性電路系統的狀態空間模型自動提取方法,能夠提取出能控規范形和能觀規范形兩種基本的狀態空間模型。該方法采用頻域分析法和改進節點法,解決了復雜電路的傳遞函數難以直接求取的問題。在MATLAB平臺上實現了提取系統,通過實例表明,該提取系統操作簡單、運行結果準確可靠,為線性電路的分析提供了有力工具。

