歸一化分割算法在路網劃分中的敏感度分析

陶黎明， 盧守峰， 江勇東

(長沙理工大學 交通運輸工程學院, 湖南 長沙 410114)

針對復雜的交通網絡拓撲關系和現實交通荷載分布，路網的子區劃分為交通管理與控制提供了思路。通過路網劃分來提取系統內部具有強關聯性的子區，服務于交通狀態的把握和子區信號的控制，從而提高交通運行效率。目前，基于各種理論路網劃分方法的研究取得了一些成果，但缺乏對于劃分方法本身特性的客觀認識，導致對其特性了解不全面和應用不充分。Walinchus[1]提出交通控制子區的概念以來，路網劃分的相關研究一直備受關注。其中，對于各種劃分方法的應用研究集中在交通信號控制子區[2-3]。在區域交通狀態分析方面，Geroliminis[4-5]等人研究了路網平均密度與平均流量相關性，并提出了能反映區域交通網絡狀態特性的宏觀基本圖(macroscopic fundamental diagram，簡稱MFD)概念。利用實測數據創建宏觀交通基本圖已成為研究的熱點。盧守峰[6]等人對利用線圈檢測器數據和出租車GPS數據創建的宏觀交通基本圖進行了研究。Geroliminis[7-8]等人通過對實測數據和模擬數據創建宏觀交通基本圖進行研究，發現：交通網絡中車輛密度的空間分布是影響MFD離散度和形狀的關鍵因素。為了得到更準確的MFD， Ji[9]等人基于路網劃分的思路，提出利用歸一化分割(Normalized cut，簡稱為Ncut)方法進行路網劃分，將交通網絡劃分為車輛密度分布均質性較高(即密度方差較小)的子區。

歸一化分割屬于譜聚類算法的一種，最早應用于圖像的分割[10]。該方法通過相似度函數計算權重后建立Laplace矩陣，并通過求解系統特征函數進行劃分對象的聚類[11]。在實際應用中，由于不同的相似度函數具有其自身的特性，聚類結果往往會依賴于相似度函數[12]。歸一化分割算法應用于路段密度屬性劃分路網時，其相似函數對路網密度分布的變化不敏感，導致路網在不同密度分布時的劃分結果都相同。為創建性能良好的MFD，作者擬對劃分路網的歸一化分割算法進行研究，對其相似函數利用懲罰系數法進行敏感度分析，為該算法的應用提供參考。

1 歸一化分割算法簡介

在歸一化分割中，先將交通網絡作為無向圖G，路段作為節點。其中，每個節點i具有對應的密度di屬性[9]。建立的鄰接矩陣{a(i,j)} (只有0或1 2個值)代表的是每對路段之間的相鄰關系。當a(i,j)=1時，表示路段i和j相連，反之亦然。為了保證路網的空間連接，將路段之間的有效值定為1，同時，定義路段i和j之間的權重相似度函數w(i,j)，其表達式為：

(1)

(2)

(3)

其中：Ncut(A,B)的最小化和Nassoc(A,B)的最大化2個目標可以被同時實現。兩者遵循的約束為：

Nassoc(A,B)=2-Ncut(A,B)。

(4)

準確求解Ncut是一個多項式非確定性的問題，但可通過求解實值域上的特征值系統，有效逼近離散解。歸一化分割的計算思想來自譜方法，其在劃分城市交通信號控制網絡小區中也得到應用[3]。歸一化分割的步驟為：

1) 給定一個從運輸網絡中建立的無向圖，并對連接路段的鄰接矩陣設置權重w(i,j)，得到矩陣C，作為2個路段之間相似性的度量。

2) 建立節點權重的Laplace矩陣F(設對角矩陣D，對角線權重為行或列權重的和F=D-C)。

3) 對矩陣系統D-0.5FD-0.5求解特征值，選取第二小特征值，并求取對應特征向量。

4) 從小到大對特征向量進行排序，根據向量是否大于0將路網劃分為2部分。

在歸一化分割過程中，為了評估和比較不同劃分后的聚類情況，引入評價指標[8]：

(5)

式中：K為區域全部子區的數目；NA和NB均為子區內路段的數量。

此外，評估簇A內的路段聚類情況的計算公式為：

(6)

NSNK(A,B)=min{NSK(A,M)|M∈

Neighbor(A)}。

(7)

其中：Neighbor(A)為空間上與集群A相鄰的子區。在該指標中，NSK(A,A)表示的是集群內的相似度，NSK(A,B)表示的是不同集群之間的相似度。如果2個集群在空間上不相鄰，即使它們的路段車道密度很接近，也會被成功分區，因此，只要測量該子區與其相鄰子區之間的相似度。又由于A可能有多個相鄰子區，因此選擇與A最相似的一個進行對比計算。整體分區的評價利用全部子區NSK(A)的平均值ANSK來評估。

(8)

式中：C為劃分的子區集合；K為子區的數量。

ANSK越小，表明劃分越理想。NSK評估度量可以等價地用集群中的路段車道密度方差和平均密度來表示，其計算式為：

NSK(A,B) =var(A)+var(B)+

(uA-uB)2。

(9)

式中：uA為子區A的路段平均密度；uB為子區B的路段平均密度。

同時，可以得到：

(10)

在式(10)中，相鄰不同子區的平均密度差越大，評價的子區內部方差越小，則NSK越小，表明該子區劃分效果越好。由于一個具有較小方差和NSK的集群可能伴隨著一個具有較大方差和NSK的相鄰子區，因此，整區劃分的評價用NSK的平均值來評估。也可以使用集群的總方差來評估整區劃分的質量，其計算式為：

(11)

歸一化分割算法的優勢有：①歸一化分割是基于圖論的分割算法，圖像的線條和色彩與路網的路段荷載具有相同的關系特征；②該分割方法可以避免劃分出大小迥異的路段集群，同時，可以產生節點規格相近的子區；③它可以實現感知性的編組，即利用圖形最主要、最明顯的成分對全局進行分割提取；④可保證劃分的路段集群在空間上緊湊連續；⑤該分割算法在路網劃分中可以有效實現。

2 敏感度分析

2.1 懲罰系數量級對劃分結果的影響

為了研究歸一化分割對于路網密度變化的敏感性，本研究基于浙江紹興柯橋城區道路的車牌照數據進行了路網劃分試驗。由CUPRITE模型[13]計算得到路段密度，其單位為輛/m。該模型在道路上、下游車輛數據統計上已得到深入驗證，并被廣泛應用。初始路網和一次初始劃分的結果如圖1所示。

圖1 初始路網和一次劃分結果Fig. 1 Initial road network and first division result

初始路網由39個交叉口和62條路段構成，區域面積約7.36 km2。將1 d中6∶10-21∶50的時段取10 min為間隔，提取了94個時間間隔，并基于密度方差最大的第70個時段(17∶40-17∶50)路網密度進行了一次分割。對所有時間段進行劃分后，發現94次劃分結果完全相同。但1 d中的不同時段，路網的道路密度方差是有明顯變化的，如圖2所示。

圖2 路網密度方差與時間的變化Fig. 2 The change of network density with time

對歸一化分割中的相似度函數添加了懲罰系數α，將相鄰路段相似度權重w(i,j)設計為 exp(-α(di-dj)2),并通過調整其數量級，對劃分結果進行了研究。最初劃分中的密度單位取輛/m，(di-dj)2的數量級為10-4。通過依次調整α，將α設為100～104，當α=103，即α(di-dj)2的數量級為10-1時，劃分結果出現了變化,如圖3所示。

圖3中，橫坐標代表94個時間段，縱坐標為路段編號，白色和黑色表示對應編號隸屬于的不同子區。比較不同α數量級下的劃分效果，可以發現：當相似度函數的量級過小時，其對路網密度的分布不敏感，劃分結果固定。同時，當路網劃分結果出現變化時，密度方差較大的早、晚高峰時段子區的臨界路段波動很大，劃分效果對密度分布變化的敏感度加強。表明：歸一化分割的劃分效果對權重指數的數量級存在依賴。為了進一步對比不同α量級下相似函數對密度分布的敏感性，驗證其指數對數量級的依賴，同樣，基于第70個時段下的路網密度，進行了具體劃分并計算了相應評價指標。不同α數量級下的路網具體劃分如圖4所示。

圖3 不同α數量級下的路段子區分布Fig. 3 The distribution maps of the road section under different orders of magnitude alpha

從圖4中可以看出，不同α數量級下的劃分結果均不同。同時，計算得到劃分子區的評價指標見表1。

圖4 不同α數量級下的路網具體劃分Fig. 4 Specific division diagrams of road network with different orders of magnitude alpha

懲罰系數車輛密度平均值/(輛·m-1)方差/(輛2·m-2)子區相似度路段數/條總方差/(輛2·m-2)相似度平均值100,101,102 (子區1)0.039 1 3.25×10-40.928 9 330.020 320.936 5 100,101,102 (子區2)0.032 4 3.31×10-40.944 0 29--103 (子區1)0.039 2 3.35×10-40.958 2 320.020 290.935 6 103 (子區2)0.032 5 3.19×10-40.913 0 30--104 (子區1)0.038 9 3.02×10-40.754 2 480.019 160.793 0 104 (子區2)0.026 0 3.33×10-40.831 7 14--

從表1中可以看出，當劃分結果出現變化后，隨著α數量級的增加，子區內路段的密度、方差、總方差及相似度平均值均降低了。劃分效果的優化表明：歸一化分割的相似函數對路網中路段密度的分布敏感度提高了，驗證了其劃分結果對相似度函數的指數量級存在依賴。這對于歸一化分割算法在不同應用中具有實際參考價值。

2.2 相似函數圖像分析

為了分析權重對相似函數圖形的影響，α取100,103,105和107, 分別繪制了函數exp(-αx2)的圖像，如圖5所示。

從圖5中可以看出，歸一化分割算法的相似度函數在初始α=100時，其函數在變量較小時斜率絕對值過小，對于變量的變化不敏感，導致其在劃分應用中對于不同密度分布情況結果相同。但隨著懲罰系數量級的增加，函數圖像逐漸變窄變陡，變量對應的斜率絕對值變大，對不同變量的感知力增強，使得不同密度方差下的子區劃分產生了差異。當α=107時，函數圖像僅在0附近很小的區間有值，其他均趨于0。這與實際試驗中利用Matlab求解矩陣系統特征向量時出現無效值錯誤相吻合。因此，在應用歸一化分割算法時，其劃分結果對相似函數的指數量級存在著依賴。量級過小，會導致其對劃分對象屬性變化不敏感；量級過大，會帶來求解困難。經試驗驗證，在MFD創建的路網劃分應用中，其相似度函數的指數-α(di-dj)2的整體量級控制在100到101比較合適，即懲罰系數α取104～105。

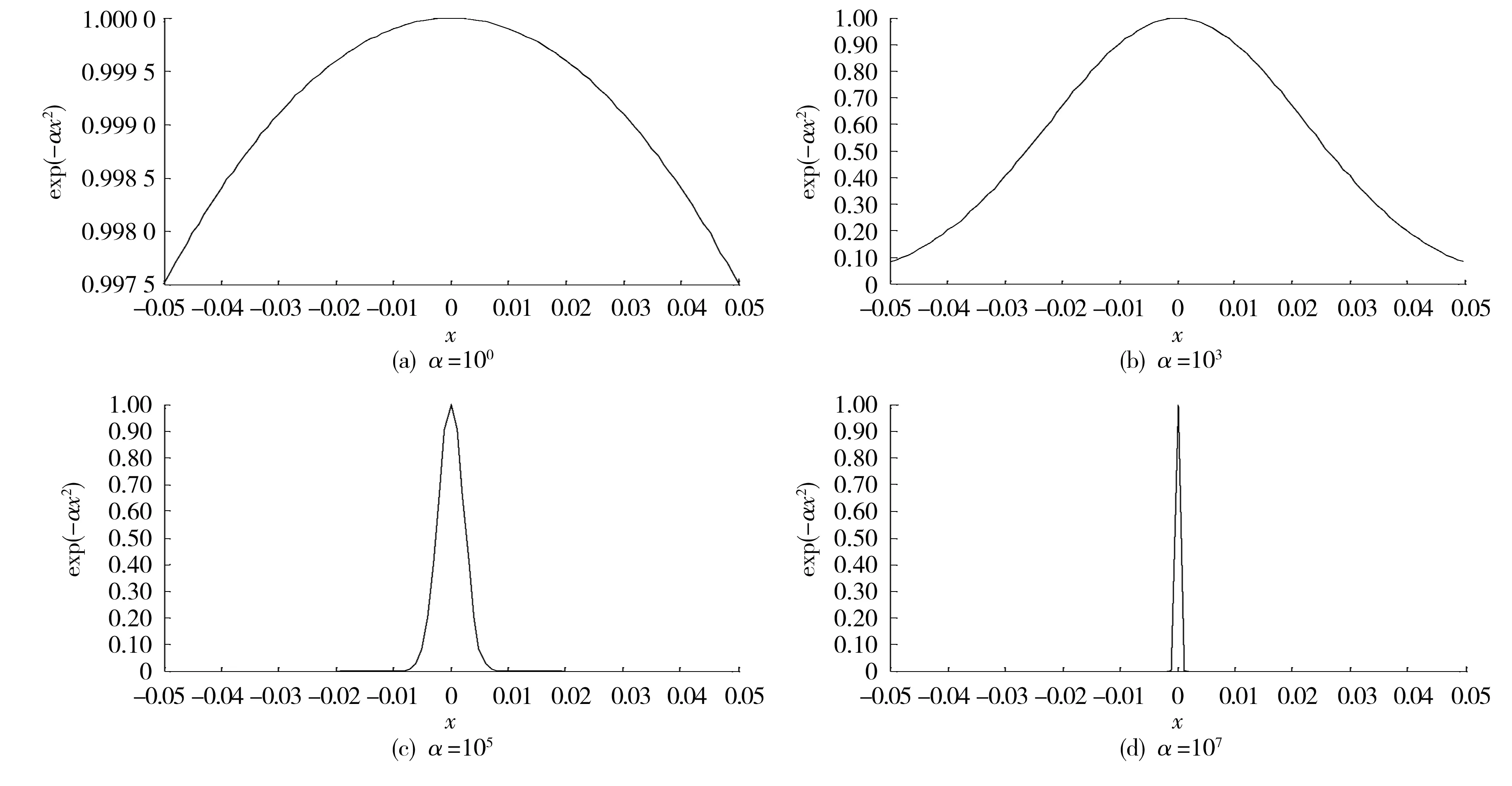
圖5 exp(-αx2)函數圖像Fig. 5 The image of exp(-αx2)function

2.3 宏觀交通基本圖分析

考慮到歸一化分割算法在MFD創建中應用的有效性[9]，對其劃分的第70個時段的路網子區進行了宏觀基本圖的分析。路網劃分前、后MFD的對比如圖6所示。

圖6 α取104時，劃分前、后MFD的對比Fig. 6 The MFD contrast of the network before and after the partition

從圖6中可以看出，歸一化分割后各子區的最大流量是不同的。該結論為精細化分析交通路網運行狀況和交通管控措施提供了依據。

3 結論

由于歸一化分割算法可以將路網劃分為密度分布均質性更高的子區，提高宏觀基本圖的準確性，但劃分敏感度在相似度函數的指數量級上存在依賴。因此，本研究通過懲罰系數法，對歸一化分割算法進行了不同指數量級下的敏感度分析，通過比較劃分后子區路網的評價指標，驗證了數量級會對劃分結果產生重要影響。同時，對不同指數量級產生敏感度變化影響的原因進行了函數曲線分析，表明了其產生影響的原因。基于歸一化分割算法在實際路網劃分應用中的有效性，以及其相似函數的敏感度特點，提出：在實際應用中，應根據劃分目標和劃分對象的屬性，合理控制其相似函數的指數量級。