切比雪夫不等式及其應用
2018-10-11 08:31:18
新教育時代電子雜志(教師版) 2018年29期
(北京交通大學附屬中學 北京 100081)
一、基礎理論知識
隨機變量:
設X=X(ω)為定義在樣本空間?上的實值函數,則稱X 為隨變量。若它僅取有限個或可列個值,則稱其為離散型隨機變量。若它的可能取值充滿數軸上的一個區間( a,b),則稱其為連續性隨機變量。[1]
分布函數:


二、切比雪夫不等式的應用

證明:由于{Xn}相互獨立,從而有:
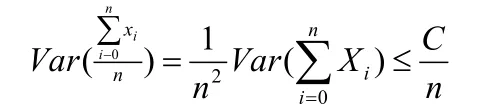
由切比雪夫不等式可得:

從而可得到:
結語
由上只是簡單舉例分析了切比雪夫不等式在證明常數方差為零,估值,依概率收斂上的應用,除了這些,切比雪夫不等式在證明馬爾科夫不等式上也有相應的應用。這里不再贅述。

