基于小波和獨立成分分析的去噪自適應算法

白文平，劉宗昂，，魯加國

（1.91550部隊，遼寧大連116023；2.中國電子科技集團第38研究所，合肥230088）

在圖像去噪領域，由于含噪圖像的來源不同，所含噪聲的種類和數量不確定，所以難以尋求一個通用的方法解決各種圖像去噪的問題。目前，圖像去噪在不同的應用領域有著多種不同的方法。

早期的多數去噪方法屬低通濾波器的類型，將具有高頻特性的圖像噪聲在空間域或變換域濾除[1-2]。近期有研究熱點集中在非線性變換域去噪[3-5]，然而，無論是傅里葉變換在頻率域的平滑，還是小波變換在頻率域和空間域上的雙管齊下，雖能達到去噪的目的，但同時也造成了目標邊緣模糊，且沒有自適應性。

在非線性變換領域的研究中，利用高階統計方法的獨立成分分析技術（ICA）[6-7]，因其具備數據適應性特點，在去噪應用中效果顯著而得到快速的發展[8-9]。它不需要提前獲得噪聲的類型和圖像的信息，就能得到比較準確的結果，這樣的優勢自然使ICA技術成為了一個熱點的研究方向。

目前流行的用ICA技術來消除復雜噪聲的方法主要有：適應性主成分分析（PCA）方法[10-11]、稀疏編碼收縮方法[12-13]、ICA混合模型[14]、獨立子空間分析[15-16]、多分辨率傅立葉變換獨立成分分析等。本文提出一種改進的小波ICA去噪算法，以提高去噪效果。

1 ICA模型

借助PCA對ICA進行說明。假設特征向量x由2種成分x1與x2組成：

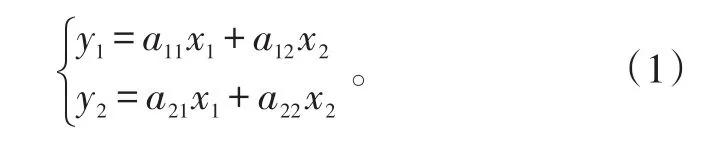
使用PCA方法對特征成分進行分離的方法是：通過旋轉坐標軸，尋找新的坐標軸方向，使觀測數據在新的坐標軸上的投影分量具有最大標準差。此坐標軸方向即主方向，觀測數據在該方向上的投影即主成分。顯然，主方向上攜帶了最多的原始數據信息，主方向上的投影稱為主成分，可以用來逼近原始數據成分。坐標軸旋轉、平移后可表示為：

式（2）中：Cx為x的協方差矩陣；Cy為y的協方差矩陣

利用矩陣A可使其成為對角線矩陣，對角元素則為每個主成分Ym的方差，所有的主成分是互不相關的。上述就是利用PCA方法進行主要成分分離的本質。ICA被研究者們認為是PCA的一個泛化，它不僅僅利用二階卷積，而是利用了更高階的卷積來對相互獨立的成分進行分離。互不相關的條件比相互獨立的條件弱，但對于高斯分布的隨機變量而言，互不相關等同于相互獨立。

因為多個隨機變量的總體分布，比其中一個隨機變量的分布更接近高斯分布[17]，所以可以先利用“負熵”來計算變量的非高斯性，用來表示獨立成分的分離程度，再用ICA方法尋找缺少先驗信息的混合矩陣的逆。負熵表示為：

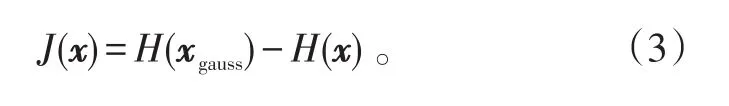
式（2）中：H(·)表示香農熵函數；xgauss為具有相同協方差矩陣的高斯隨機變量x的集合。

通過概率密度估計熵的近似值：

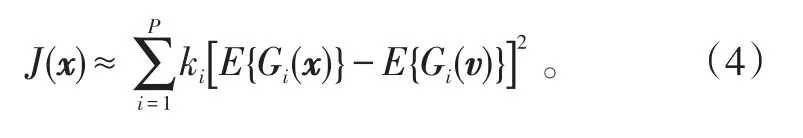
式（4）中：E為理想期望值；x和v為具有0均值、單位方差的隨機變量；v同時為高斯隨機變量。

使用式（4）前，須對給定的隨機變量x進行標準化，比較流行的FastICA算法通常利用2個比較優秀的非二次函數G1進行較好地近似，以實現熵最小化。

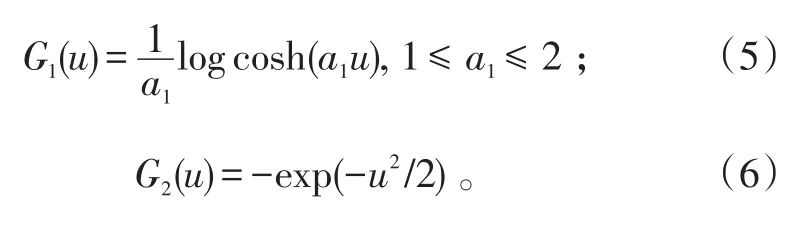
2 小波變換和ICA相結合的圖像去噪算法

2.1 小波降維

垂直投影[18]技術雖然能夠將圖像維度降為一維信號，從而提高圖像去噪的效率，但是對于某些圖像而言，一維信號仍然顯得過大。

為了解決這樣的問題，將一維信號作為特征向量，利用Morlet小波變換進行降維。小波變換為圖像處理工程師提供了一種非常靈活的工具，它不僅取代了傅里葉變換，而且發展為體系完備的一套數學工具。本文為了降低計算復雜度采用一維小波變換來降低特征向量的維度。

小波濾波器通過卷積將信號分解為高頻與低頻成分：

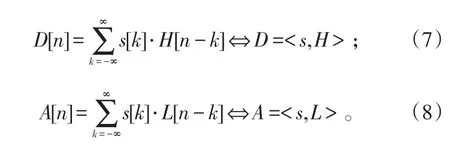
2.2 小波ICA濾波器

獨立成分分析模型的輸入只能是矩陣，于是在小波ICA濾波器中，利用小波降維設計輸入矩陣。

圖像中噪聲成分的比例可能隨環境的變化而改變，就像獨立成分變量的混合比隨帶通濾波器窗口位置的不同而變化。圖1中，s1、s2與s3為觀測數據所包含的三個獨立分量。窗口T1與T2表示與兩個不同的帶通濾波器觀測窗口，顯然，從T1與T2帶通濾波器觀測窗口中看，s1、s2與s3的混合比例是不同的。

令s1與s2為信號x的2個獨立分量，x經線性變換a、b后得到xa、xb，s1a與s1b分別表示來自不同觀測xa與xb中s1的分布，s2a與s2b分別表示來自不同觀測xa與xb中s2的分布。在獨立成分分析過程中，最終將利用s1a與s1b或s2a與s2b的相關性以及s1a與s2a或s1b或s2b的獨立性，從觀測數據中將s1與s2分離出來。需要注意的是，我們對觀測數據中的各成分分量并不存在先驗知識，只是將信號中的分量處理成包含盡量多的分量的數據。ICS濾波器就是將小波變換代替上述線性變換，成為一種帶通濾波器，但是因為混合圖像成分中的獨立成分變量以及圖像數據的缺失，ICS方法的效果不及ICA方法。

為了從理論上說明小波ICA濾波器檢測獨立成分的可行性，需有兩點作為理論支撐：

首先，必須證明s1a與s1b是相關的，s1a與s1b間的相關函數為：

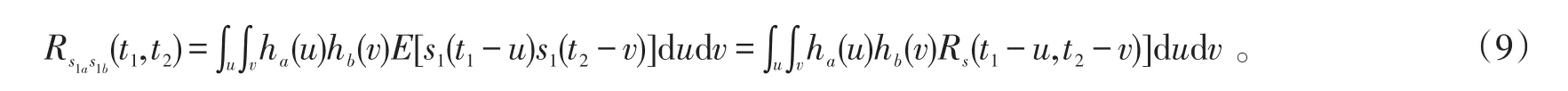
其次，要證明s1a與s2a是獨立的。令

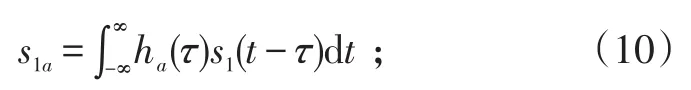
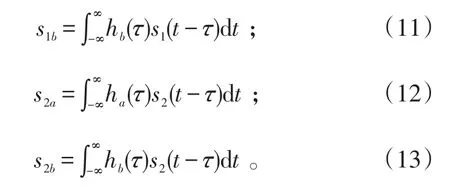
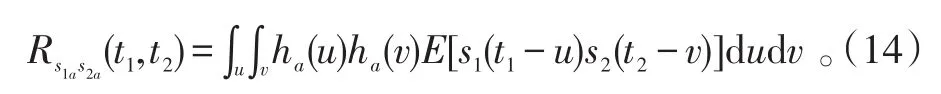
因為有E[s1(t1)s2(t2)]=0，則：

因為s1(t)與s2(t)相互獨立，s1a與s2a在任何高階序數下都不相關，s1a與s2a相互獨立。同理可得s1b與s2b也相互獨立。

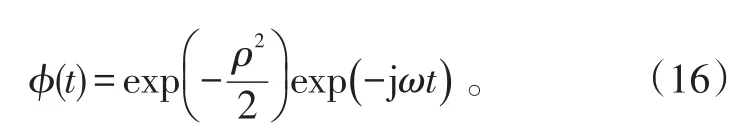
小波變換的定義為：

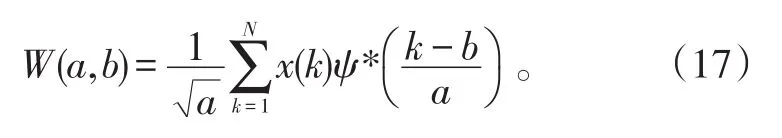
式（17）中：a為擴張參數；x(k)為數據信息；*表示聯合操作。

本文使用基于小波和獨立成分分析的方法消除圖像噪聲，針對的不僅僅是白噪聲，而是未知的加性或者乘性甚至是混合噪聲，被未知的混合噪聲污染的圖像很難進行去噪，在ICA的框架下需改變圖像的數理統計，修改混合標準ICA模型，調整反饋補償，使用二階以及更高階統計，采用附加ICA模型（MICA）去噪。含有混合噪聲的獨立源混合模型為：

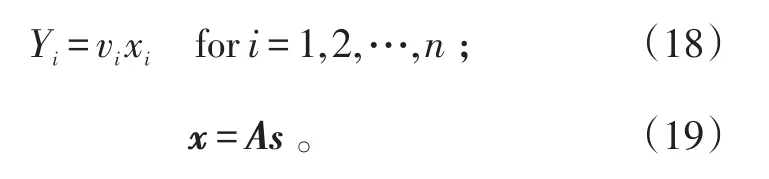
式（18）、（19）中：Y=[Y1,Y2,…,Yn]T為向量表示的含有噪聲的圖像信息；x為干凈的無噪圖像信息；為圖像中的混合噪聲向量；i代表相應像素位置；為圖像的n個獨立向量；A為混合矩陣，混合矩陣的逆稱為分離矩陣。

去噪的過程分為3個步驟：

1）白化，然后獨立成分分析發現一個非線性數據變換矩陣B，使其輸出盡可能獨立。

式（20）中：U為分離矩陣（歸一化矩陣）也就是混合矩陣A的逆；W為白化矩陣。

獨立成分分析可以通過高階圖像統計來尋求問題的解。本文使用三階卷積圖像統計的方法，經最小化求解。

2）根據觀測窗口的相關性對圖像數據與噪聲數據進行分離

3）求解混合矩陣的逆對圖像進行還原。

3 實驗及分析

使用本文提出的小波與ICA相結合的去噪算法、PCA算法和FastICA算法處理相同的噪聲圖像，比較去噪后圖像的峰值信噪比（PSNR）和平均絕對誤差（MAE）2個指標，對圖像恢復能力與細節保持能力進行評價。測試圖像大小為512×512，過濾窗口大小均為3×3。

通過使用被脈沖噪聲污染的圖像作為實驗圖像進行對比試驗，驗證了文本提出的小波ICA濾波器的效率最高。圖2顯示了對20%脈沖噪聲污染的Lena圖像的去噪結果，圖2 c）～e）中MAE分別為2.79dB、2.36dB、1.93dB。本文方法恢復的圖像效果較好，包含較低的噪聲，保留了更多的細節，并給出了最小的MAE值。

圖2 對脈沖噪聲污染的Lena圖像去噪的效果比較Fig.2 Comparison of the effects of de-noising Lena image polluted with impulse noise

表1顯示了3種方法對包含10%脈沖噪聲的圖像去噪時PSNR的結果比較。可以看出，本文方法的效果遠好于其他方法，可以得到較高的PSNR值。

為了證實本文算法的魯棒性，圖3與圖4顯示了對于包含10%～60%脈沖噪聲的圖像處理后的，相應的PSNR的比較和MAE的比較。圖3與圖4清楚地顯示了本文方法優于其他濾波器。

表1 處理10%脈沖噪聲圖像的PSNR比較Tab.1 PSNR comparison about denoising 10%impulse noise image

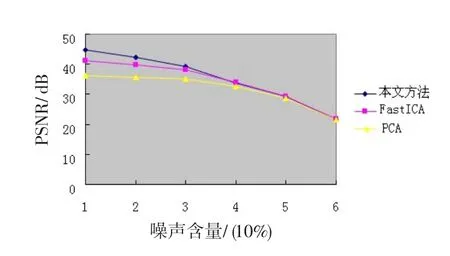
圖3 包含不同比例脈沖噪聲圖像去噪的PSNRFig.3 Comparison of PSNR contains varying proportions of impulse noise denoising

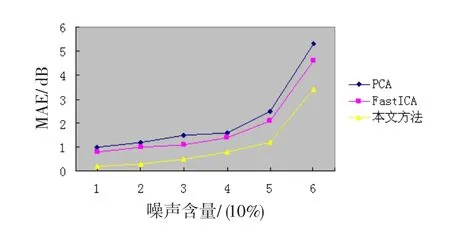
圖4 包含不同比例脈沖噪聲圖像去噪的MAEFig.4 Comparison of MAE contains different proportions of impulse noise denoising

本文比較了本方法與其他方法對混合噪聲（高斯噪聲σ=20脈沖噪聲20%）的消除效果，圖5顯示了對于包含混合噪聲（高斯噪聲σ=20脈沖噪聲20%）Lady圖像的去噪效果，如圖5所示，圖5 c）～e）中MAE分別為16.39dB、15.72dB、14.61dB。本文方法可以得到最好的可視效果，噪聲斑點最少，MAE值也最低。

表2顯示本文方法對比其他方法給出了最高的PSNR。

圖5 對包含混合噪聲Lady圖像的去噪效果比較Fig.5 Comparison of the effects of de-noising Lady image polluted with mixed noise

表2 去除混合噪聲的PSNR對比Tab.2 Comparison of three methods for denoising mixed noise

因為本文提出的算法要進行小波變換、獨立成分分析、計算相關性、圖像重構，在算法復雜度上高于PCA和FastICA方法，經比較在不同的去噪應用中，計算量增加了4.5%～9.7%。

4 總結

獨立成分分析是適合多源數據分析的高階統計方法，具有數據適應性的特點非常適合圖像去噪，在對噪聲類型、量級未知的情況下，能夠得到較好的去噪效果。本文先用小波變換對圖像進行分解，降低特征向量的維度，再用獨立成分分析，通過負熵值來評價隨機變量的非高斯性，根據觀測窗口的相關性對圖像與噪聲進行分離，最后求解混合矩陣的逆對圖像進行還原。對比實驗驗證了本文提出的方法在PSNR和MAE指標上效果優于PAC和FastICA濾波器，且本文方法得益于ICA的數據適應性特點，不僅對脈沖噪聲有效，對脈沖和高斯混合噪聲也同樣有效。