基于模型預測控制的混合動力汽車模式切換中的轉矩協調控制策略?

張淵博，王偉達，項昌樂，黃 琨，馬 越，魏 超，李子龍

(北京理工大學機械與車輛學院，北京 100081)

前言

近年，在環境污染和石油資源短缺的實際背景下，新能源汽車得到了越來越多企業和科研機構的青睞。目前市場上新能源車輛主要有純電動汽車、燃料電池汽車和混合動力汽車[1]。其中混合動力車輛可通過多種工作模式之間的協調切換，有效提高其燃油經濟性。然而在模式切換過程中，由于系統的不連續性等特性，仍會出現平順性差、沖擊度大等問題。本文中基于雙模混聯式汽車對該問題進行了深入的研究。

1 技術研究現狀

近年專家學者對混合動力汽車進行了大量的研究，內容包含了車身構型、能量管理和模式切換等多個方面，均取得了顯著成果，其中關于模型切換過程的主要研究成果如下。

Beck R等人基于并聯式混合動力汽車，利用模型預測控制算法通過對發動機和電機的轉矩進行動態協調分配，提出了模式切換過程協調控制策略[2]；針對模式切換過程，Sul S K等人從優化換擋規律著手，提升了機械傳動的效率，并通過電機調節離合器兩端的轉速差，減小了模式切換過程中車輛所受到的內部沖擊[3]；Nelson D J等人設計了基于PID控制的模式切換過程控制策略，利用驅動電機調速實現離合器兩端轉速的同步，降低了模式切換時離合器接合過程中的沖擊[4]。

針對模式切換過程的沖擊問題，Gu Y等人首先通過最小值原理對動力系統的轉矩進行了優化，然后基于模糊PID控制理論綜合控制離合器接合過程的執行機構速度和節氣門開度，同時利用電機轉矩補償需求轉矩和離合器輸出轉矩中的差額，顯著提升了模式切換過程中的平順性[5]；針對模式切換過程中轉矩波動大的問題，王慶年等人提出了利用電機補償的模式切換控制策略[6]；山東大學的孫靜提出了基于數據驅動預測控制的轉矩協調控制方法，通過跟蹤輸出參考序列并限制離合器的轉矩變化率，實現了模式切換時間短和沖擊度小的目標[7]。

Rizzoni G等人針對并聯式混合動力汽車，將其模式切換過程依據不同階段特性劃分成了多個子區域，并基于最優控制理論設計了不同子區域的子控制器，通過仿真驗證了該策略的有效性[8]；同樣，Soliman I S等人將雙驅動混合動力汽車的模式切換過程劃分為4個階段，針對不同階段設計了協調控制策略，并通過道路試驗對所提出的控制策略進行了驗證[9]；Kim H等人設計了并聯式混合動力汽車模式切換過程4階段控制策略，并在每階段設計了相應的擾動觀測器，通過對系統擾動的觀測與補償，提高了所提出策略的控制效果[10]。

趙治國等人針對模式切換過程中動力耦合所造成的汽車平順性問題，提出了一種無擾動模式切換控制策略[11]；李亮等人針對并聯式混合動力汽車模式切換中離合器接合過程，依據離合器的不同狀態將其分為5個階段，并對其中關鍵的滑摩階段設計了基于H∞魯棒控制和基于L2增益魯棒控制的分層控制器，最后通過試驗驗證了所設計控制器的有效性和魯棒性[12]。

綜上所述，目前模式切換控制研究的對象多以并聯式混合動力汽車為主，對雙模混聯式混合動力汽車模式切換過程研究較少，本文中針對雙模混聯式汽車，深入研究了其在不同機電混合驅動模式的模式切換過程，建立了功率耦合機構的等效模型，提出了基于模型預測控制的轉矩協調控制策略。

2 等效模型

本文中所研究的機電復合傳動(electro-mechanical transmission，EMT)系統如圖1虛線框所示。該系統由發動機、電機、功率耦合機構等組成。

圖1 機電復合傳動結構簡圖

功率耦合機構如圖2(a)所示，根據離合器C1和制動器BK的工作狀態，功率耦合機構可以實現EVT1和EVT2兩種機電混合驅動模式，EVT1模式下離合器C1斷開，制動器BK接合，該模式適用于低車速狀態下大轉矩需求的工況；EVT2模式下離合器C1接合，制動器BK斷開，該模式適用于高車速狀態下小轉矩需求的工況。

綜合考慮發動機、電機和行星齒輪機構的轉動慣量，建立從EVT1模式到EVT2模式的模式切換過程中的動力學模型：

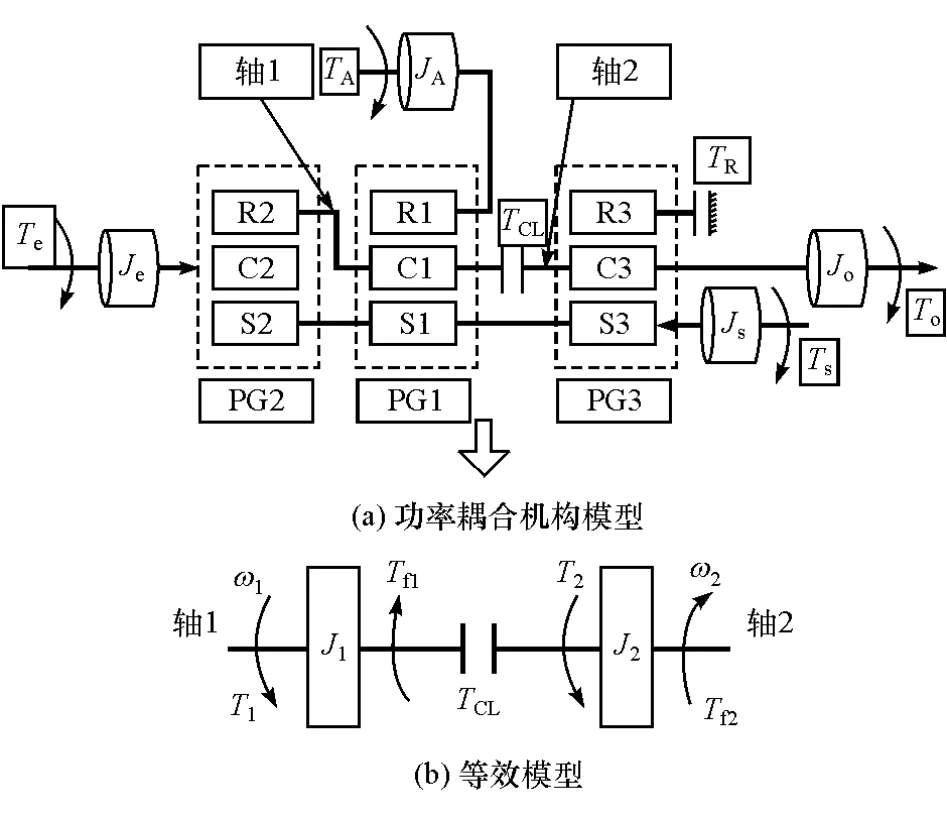
圖2 機電復合傳動拓撲結構

式中：JA為電機A轉動慣量；JB為電機B轉動慣量；Jo為輸出軸的等效轉動慣量；Jsi，Jri，Jci(i＝ 1，2，3)分別為太陽輪、齒圈和行星架的轉動慣量；Tf為負載轉矩；Tsi，Tri，Tci(i＝1，2，3)分別為太陽輪、齒圈和行星架的轉矩；TCL，TBK分別為離合器C1和制動器BK的轉矩；ωc1，ωr3分別為PG1行星架和PG3齒圈的角速度；ωA，ωB分別為電機A和電機B的角速度；ωi為功率耦合機構的輸入角速度。

為方便研究離合器動態特性對機電復合傳動EVT模式切換的影響，將功率耦合機構模型簡化為圍繞離合器主被動端的等效模型，如圖2(b)所示。圖中：J1，J2分別為軸1和軸2的等效轉動慣量；ω1，ω2分別為軸1和軸2的角速度；T1，T2分別為軸1和軸2的等效轉矩；Tf1，Tf2分別為軸1和軸2上由負載引起的阻力矩。

等效模型軸1的動力學方程：

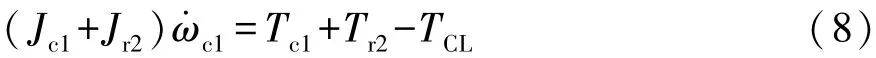
等效模型軸2的動力學方程：

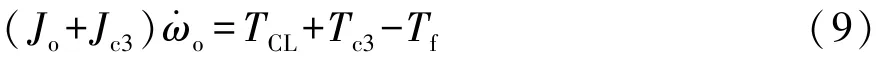
式中：行星架C1的角速度為軸1的角速度，即ω1＝ωc1；輸出軸的角速度為軸2的角速度，即 ω2＝ωo。

發動機和電機的角加速度由下式確定：

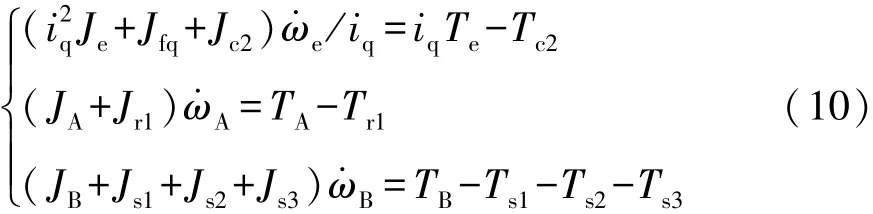
式中：iq為前傳動齒輪傳動比；Jfq為行星排內部的轉動慣量；Je為發動機的轉動慣量。

各部件角速度之間的關系式為

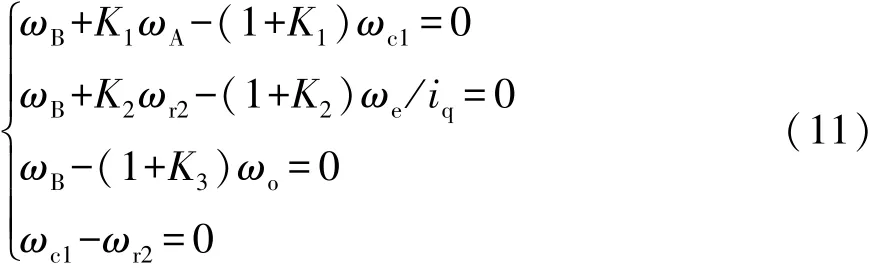
式中K1，K2和K3分別為PG1，PG2和PG3的特性參數，其為該行星齒輪齒圈的齒數和太陽輪的齒數之比。

各部件的轉矩關系式為

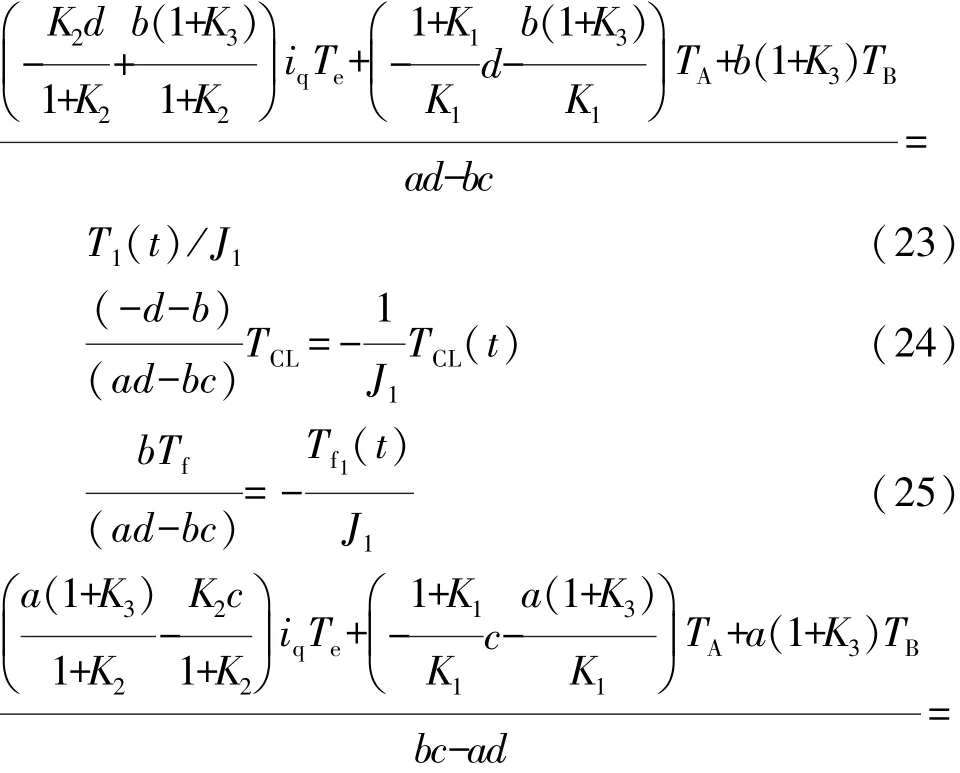
結合上述公式，可得軸1的轉矩方程為

由于行星排內部的慣量較小，在此忽略不計，則有

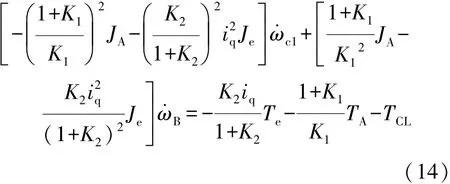
由式(11)可得

由式(14)可得

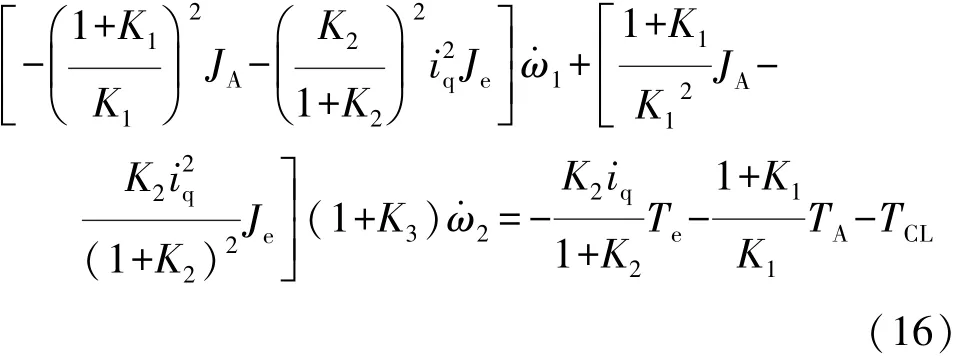
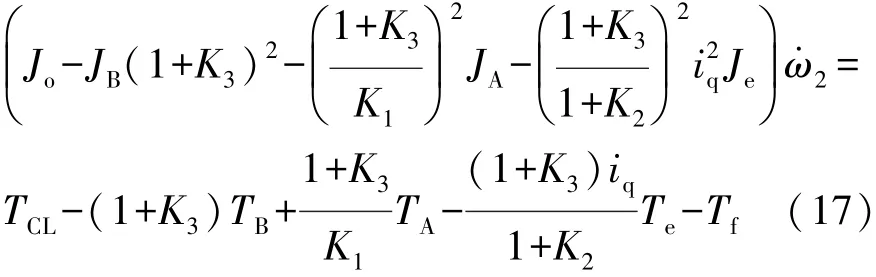
整理可得

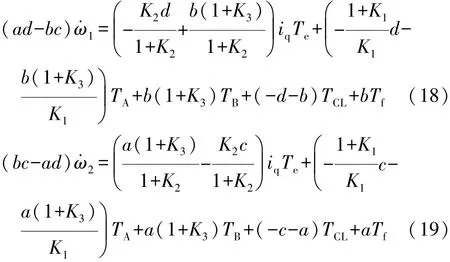
其中

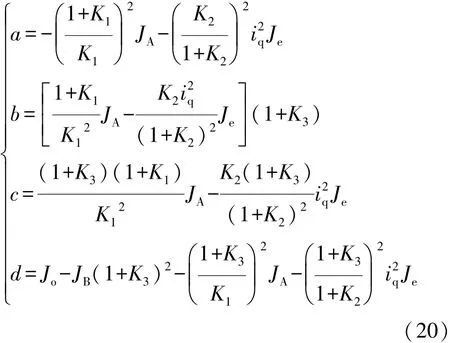
根據圖2(b)，機電復合傳動等效模型的動力學方程為

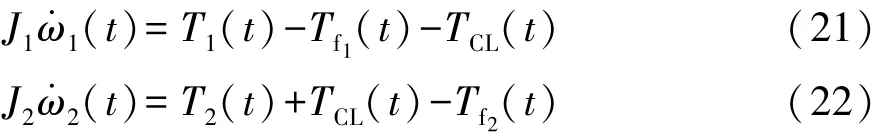
因此，圖2(a)和圖2(b)中轉矩和慣量的等效關系為

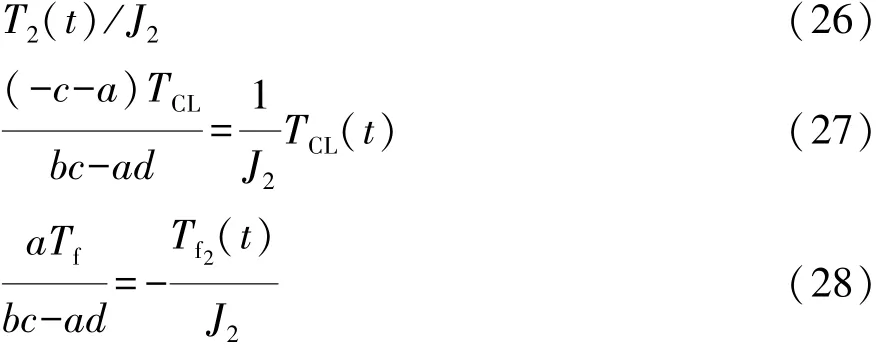
3 基于模型預測控制的轉矩協調控制策略

模型預測控制是一種在線滾動的優化算法，它在每一個控制步長，都會求解相應預測時域內最優控制問題，并將最優控制序列的首行元素作為控制變量輸出，從而達到預估的控制效果，該方法可以預測被控系統的性能狀態，適用于比較復雜且多目標的控制過程[13-14]。本文中針對離合器接合過程中的沖擊和滑摩損失相矛盾的問題，基于模型預測控制方法設計了兩者兼顧的轉矩協調控制策略。

3.1 面向離合器接合過程的動態方程與問題描述

根據離合器的主從動盤轉速和位置，離合器接合過程可劃分為以下3個階段。

(1)離合器分離階段

該階段主從動盤未接觸，相互之間不傳遞轉矩，此時運動方程為

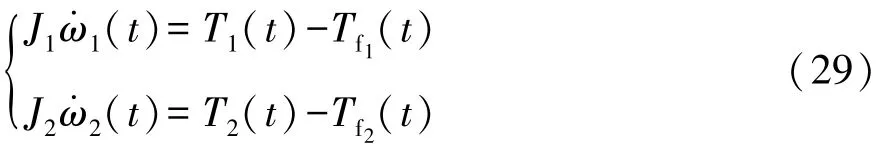
(2)離合器滑摩階段

當離合器主從動盤開始接觸，但兩者轉速不一致時，離合器處于滑摩階段，此時，隨著執行機構的操作，離合器主從動盤之間壓力逐漸增大，傳遞轉矩也隨之增大，該階段運動方程為

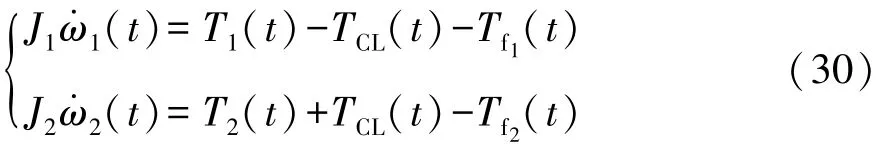
(3)離合器同步階段

當離合器主從動盤接合且兩者轉速一致時，離合器處于同步階段，該階段運動方程為

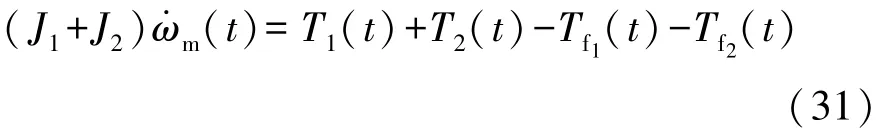
式中ωm為離合器同步階段主從動盤的角速度。此時離合器可看做剛性連接，則有

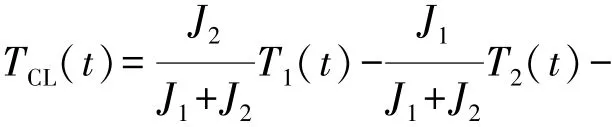
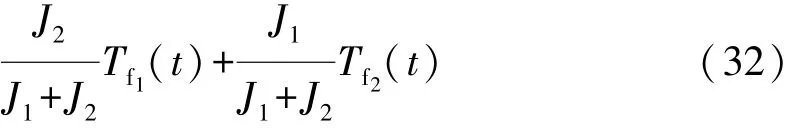
基于控制理論，下面對式(14)和式(15)中的變量進行相應的處理。狀態量可定為x1(t)＝ω1(t)，x2(t)＝ω2(t)；輸入量為 T1(t)＝u1(t)，T2(t)＝u2(t)，TCL(t)＝u3(t)；輸出量為 y1(t)＝ x1(t)，y2(t)＝x2(t)；擾動量為 d1(t)＝ Tf1(t)，d2(t)＝ Tf2(t)。

3.2 過驅動系統控制分配

經過處理后，在滑摩階段的狀態空間方程為

其中：x＝[x1(t)x2(t)]T；u＝[u1(t)u2(t)u3(t)]T

由于3個輸入轉矩皆存在上下限，應對其進行約束，其方程為

該系統控制輸入量u的維數大于輸出量y的維數，因此是一個過驅動控制系統[15]。為解決該問題，引入虛擬控制量v＝[v1v2]T，v1和v2分別為軸1和軸2上的轉矩，虛擬控制量為

因此控制矩陣B可分解為

則式(18)可簡化為

其中vmin＝[u1min-u3minu2min+u3min]T

vmax＝[u1max-u3maxu2max+u3max]T

該控制系統的整體架構如圖3所示，首先上層策略依據駕駛員操作和車身狀態發出模式切換指令，然后參考模型基于參考控制量計算出相應的參考轉速，模型預測控制器基于參考轉速和車身反饋的實際轉速，結合增廣模型及目標函數，求解出最優虛擬控制量，繼而利用最優分配策略對該虛擬控制量進行分配，最后得到實際的最優控制量，它與擾動共同作用于整車，在保證整車車速跟蹤性與平順性的同時快速完成模式切換過程。

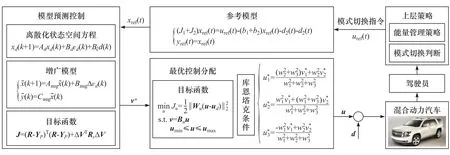
圖3 基于MPCA的轉矩協調控制框圖

3.3 參考模型

選取離合器接合后的狀態作為參考模型，離合器接合后軸1和軸2的轉速相同，系統由等效轉矩T1和T2共同驅動，使被控對象的實際輸出量即轉速跟蹤參考模型的狀態量。參考模型的動力學方程為

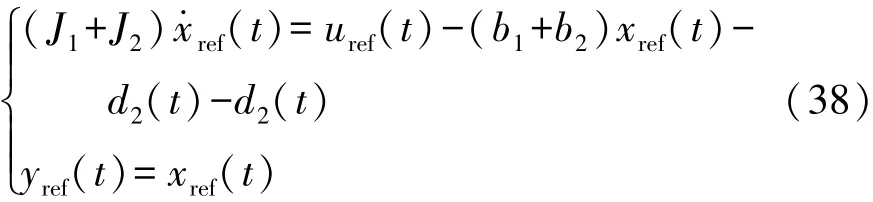
式中：xref(t)為參考轉速；uref(t)為參考轉矩，且uref(t)＝ u1(t)+u2(t)。

3.4 模型預測控制器設計

為了實時在線計算，將等效模型離散化，設定采樣時間為τs，則離合器在滑摩階段的表達式為

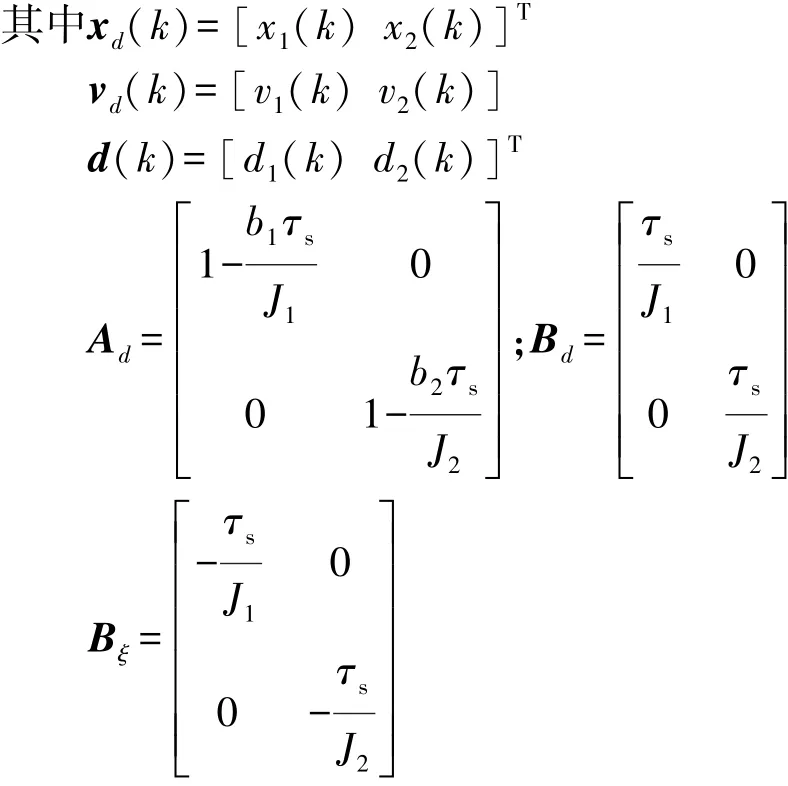
為減少或消除靜態誤差，將式(39)運用差分運算并改寫成增量模型：

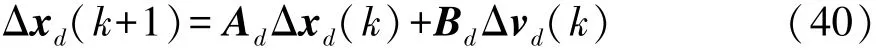
其中狀態增量為

控制增量為

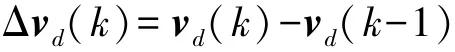
定義新的狀態變量：

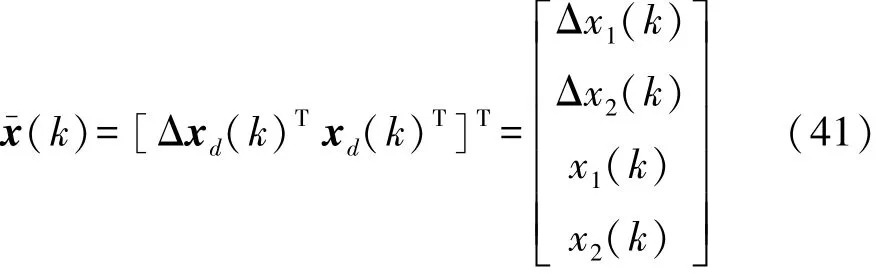
則新的增廣模型為

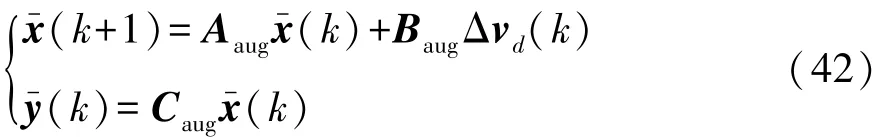
其中

模型預測控制中，每一個采樣時間內的算法運算量主要受預測時域N、控制時域M和系統模型的復雜程度3個因素的影響，本文中設定預測時域為6，控制時域為4，因此 v-(k)＝ v-(k+1)＝ …＝v-(k+5)。

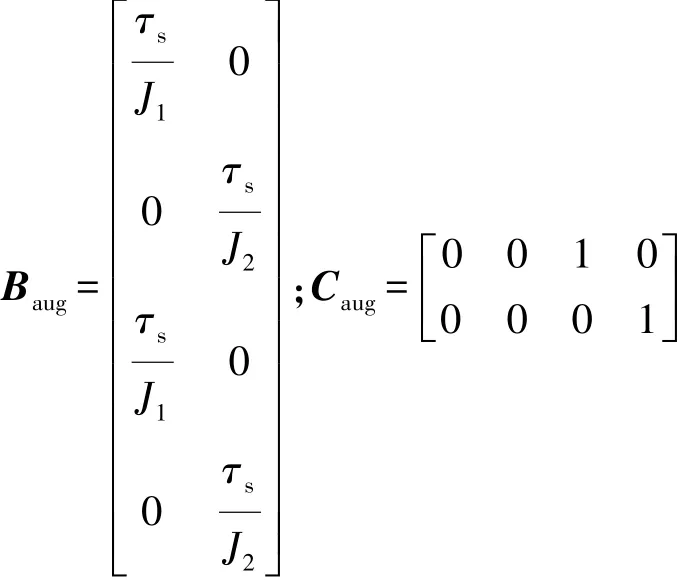
則式(42)增廣模型可表達為

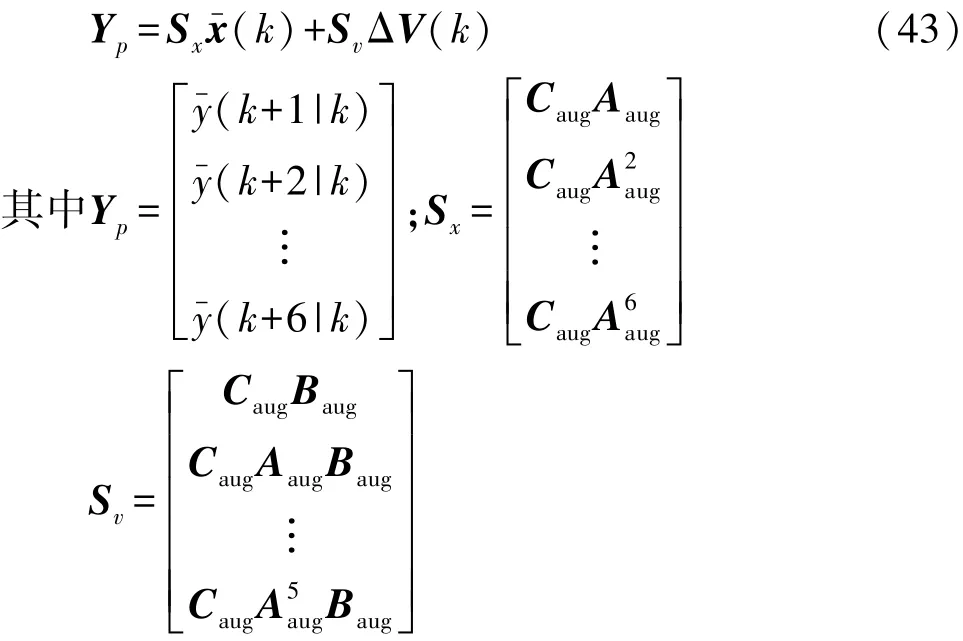
在滑摩階段，設定r(k)＝[yref(k) yref(k)]T作為輸出量y1(k)和y2(k)的參考信號，使離合器兩端軸1和軸2的轉速能實時跟蹤信號r(k)。因此，設定目標為使離合器兩端轉速和參考轉速之間誤差最小，目標函數表達式為

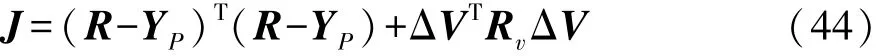
式中：R為參考信號的矢量矩陣；Rv為調節控制矢量的權重矩陣。

使目標函數最小的必要條件為

求解得到的最優控制增量ΔV為

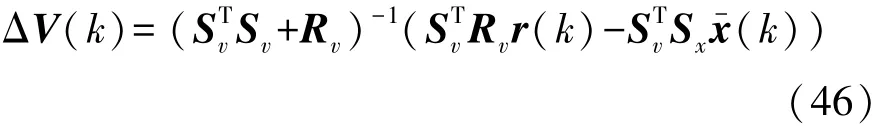
則系統當前時刻最優虛擬控制量為

3.5 最優控制分配

根據上述公式可求得的使離合器兩端轉速與參考信號誤差最小的虛擬控制量v?，該虛擬控制量仍需分配到實際控制量u即發動機和兩個電機的輸出轉矩上。為了保證離合器傳遞轉矩時的連續性，采用以控制量最小化為目標的分配方法進行優化[16-17]，優化模型為

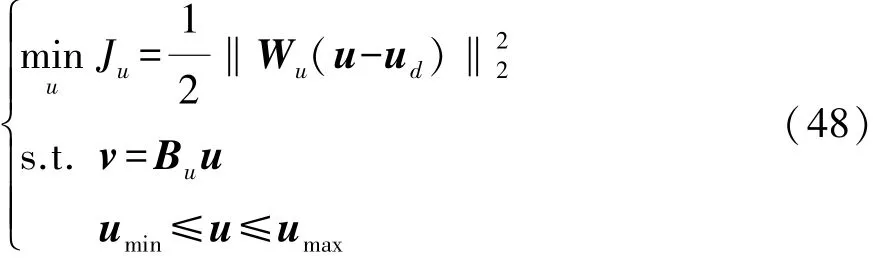
標控制量。該優化問題的拉格朗日函數為

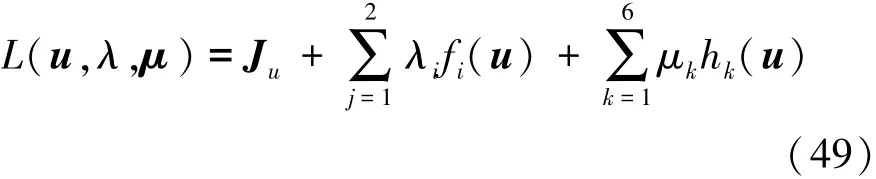
其中

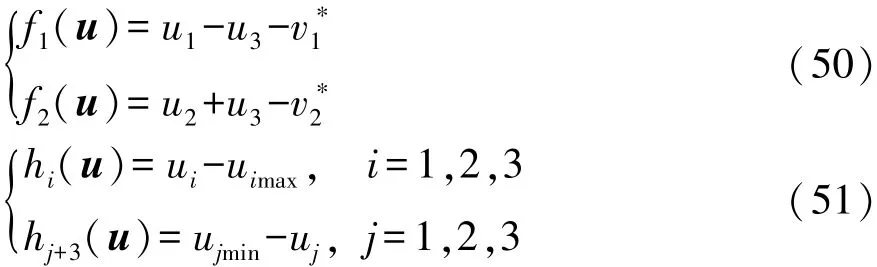
式中：fi(u)(i＝1，2)為等式約束；hk(u)(k＝1，2，…，6)為不等式約束。

采用庫恩塔克(Karush-Kuhn-Tucker，KKT)條件[18]求解此類同時存在等式和不等式約束的最優化問題：

最終求得實際最優控制量為

4 仿真與結果分析

為驗證模式切換過程中基于模型預測控制的轉矩協調控制策略(model predictive control allocation，MPCA)的有效性，采用現階段廣泛應用的基于規則的控制方法作為基準(Baseline)，用以對所提出的控制策略進行對比，由于基準控制策略不是本文研究重點，此處不再多加描述，詳細內容可見文獻[1]。仿真中設定離合器接合兩端轉速差的閾值為200r/min，控制器采樣時間為0.01s，虛擬控制量的權重矩陣為Rv＝diag(4，2)，實際控制量的加權矩陣為Wu＝diag(2，1，3)。

模型預測控制策略與作為基準的規則式控制策略的仿真結果如圖4所示。從圖4(a)和圖4(b)可以看出，模型預測控制策略通過協調控制等效轉矩T1(t)和T2(t)，有效地補償了離合器接合過程中的摩擦轉矩；由圖4(c)和圖4(d)可知，模型預測控制的離合器滑摩時間為0.42s，而規則式控制策略的滑摩時間為0.58s，減少了27.59%；如圖4(e)所示，在模型預測控制策略中車速的變化更為平緩，說明該策略下駕駛平順性更好；由圖4(f)、圖4(g)和圖4(h)可知，模型預測控制策略的加速度波動范圍為0.142～0.215m/s2，最大沖擊度為 0.15m/s3，離合器接合過程的滑摩功為1 944J，而規則式控制策略的加速度波動范圍為-0.03～0.22m/s2，最大沖擊度為14.61m/s3，且滑摩功為4 280J。表1詳細給出了離合器接合過程中MPCA與Baseline方法的仿真結果對比。

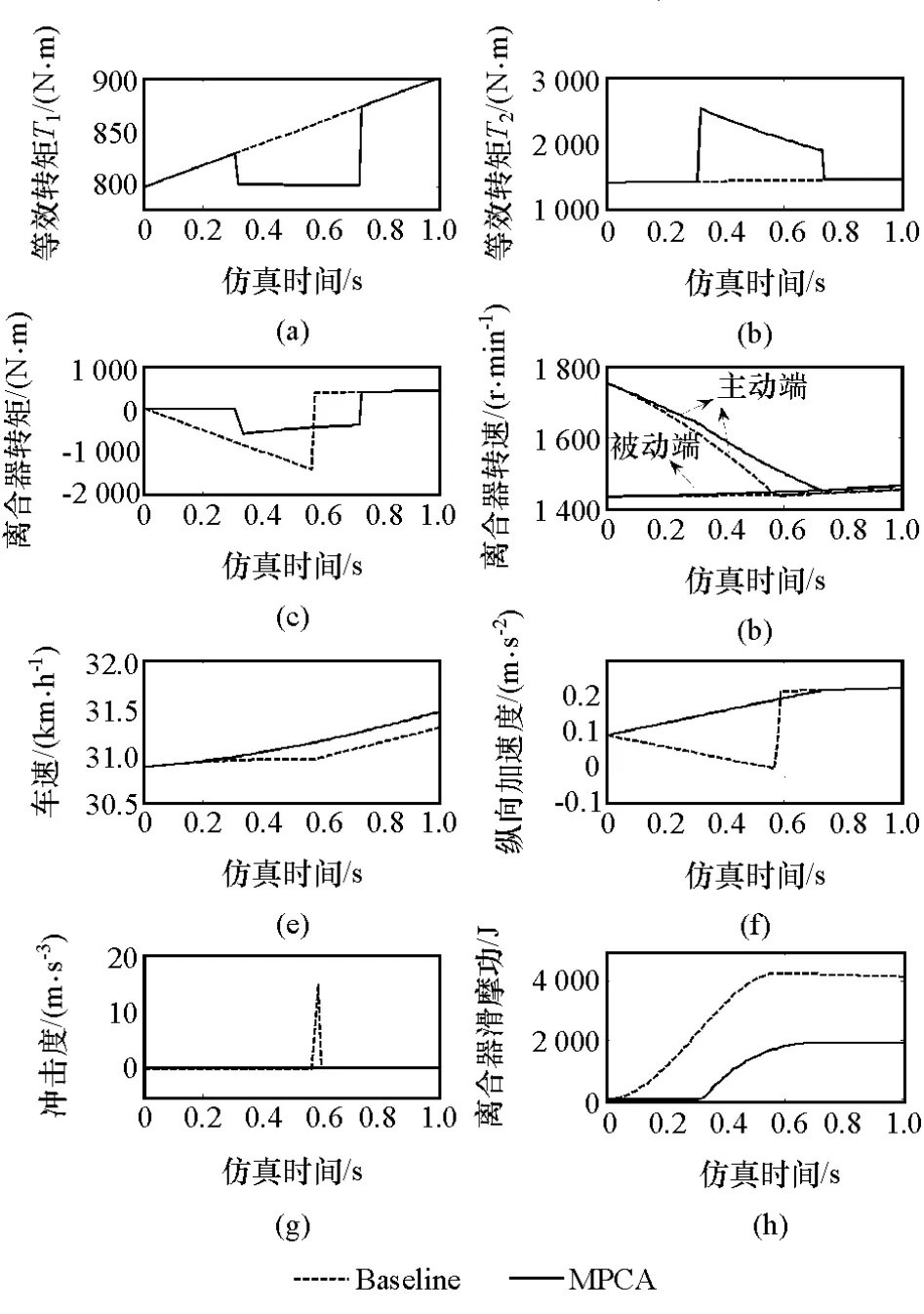
圖4 MPCA和Baseline仿真結果對比

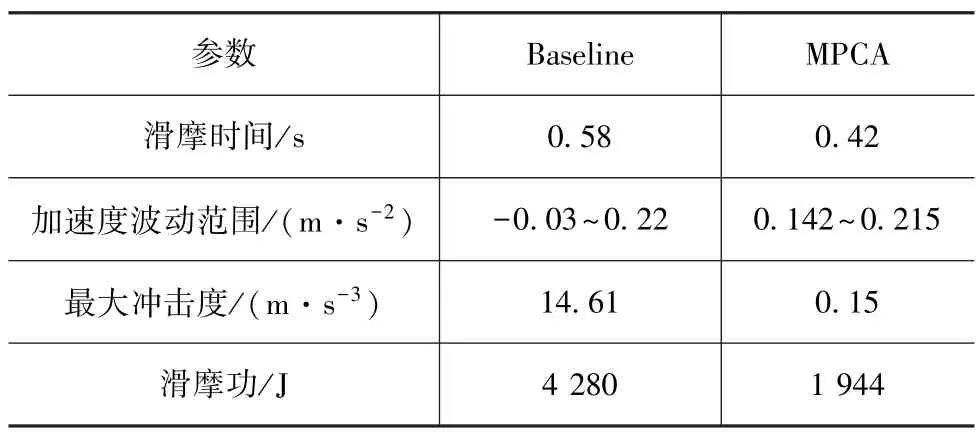
表1 MPCA與Baseline仿真結果對比

因此，本文中所提出的基于模型預測控制的模式切換過程轉矩協調控制策略能在保證車速穩步上升的同時，使加速度的波動范圍更小，沖擊度大幅度降低，且離合器的滑摩損失只有基準的45.42%。

5 結論

本文中以雙模混聯式機電復合傳動為研究對象，以改善模式切換品質為研究目的，重點圍繞離合器接合過程控制策略展開研究。首先，對本文中所研究的機電復合傳動總體結構和特性進行了分析，并采用理論與試驗相結合的方法建立了功率耦合系統的等效模型；其次，提出了以減小車輛沖擊度和離合器滑摩功為目標的基于模型預測的轉矩協調控制策略；最后，利用仿真模型，對轉矩協調控制策略進行了驗證。結果表明，機電復合傳動在所提出的模式切換控制策略的作用下，能在保證模式切換響應速度更快的同時，有效降低輸出軸的轉矩波動，并在大幅度降低車輛沖擊度的同時，減小約一半的離合器滑摩損失，因此極大地改善了模式切換品質，對于工程實踐具有一定的參考價值。