內燃機式增程器扭轉振動的建模與分析?

張立軍，闞毅然，孟德建，余卓平

(同濟大學汽車學院，上海 201804)

前言

增程式電動汽車作為一種純電動汽車，因其在技術、成本、續駛里程和相對傳統汽車在節能環保方面的明顯優勢，被認為是新能源汽車取代傳統汽車過渡期的最佳選擇之一[1-2]。內燃機式增程器主要由發動機和發電機組成，是增程式電動汽車的核心關鍵部件，增程器的扭轉振動對其軸系和連接部件的壽命、振動噪聲和工作效率，以至乘坐舒適性[3-4]有著重要影響，因此增程器扭轉振動特性的研究具有重要意義。

目前國內外學者對內燃機式增程器的研究主要集中在布局與結構設計[5]、基于動力性與經濟性的參數匹配[6]和整機振動特性與噪聲的研究[7]，而對增程器扭轉振動的研究甚少。王配分析了在發動機扭振激勵作用下，聯軸器花鍵間隙對增程器傳動軸扭振的影響[8]；楊守平等研究了柴油機軸系扭轉振動特性，對比了發動機不同工作方案下的扭轉振動角位移幅值[9]。但前期學者對增程器扭轉振動的研究主要是分析發動機激振轉矩對增程器扭轉振動影響，并未考慮發電機電磁轉矩波動對增程器扭振的影響。

據此，本文中針對某存在較明顯扭轉振動噪聲的商用車增程器，建立包括發動機、離合器和扭轉減振器、發電機和控制系統模型在內的增程器扭轉振動模型，在典型工況下對模型的工作狀態、激勵轉矩和扭轉振動特性進行分析，得出典型工況各個階段引起系統扭振的主要因素。

1 扭轉振動動力學模型

1.1 模型架構與簡化方法

內燃機式增程器主要包括發動機、離合器、扭轉減振器、發電機和增程器控制系統5個組成部分[10]，其模型架構如圖1所示。當車輛電池饋電時，控制系統會通過發電機拖動發動機，然后通過發動機驅動發電機給動力電池充電或直接通過電機驅動車輛[11]。

圖1 內燃機式增程器扭轉振動模型架構

本文中所分析的某商用車增程器是由四沖程直列四缸汽油機、離合器、扭轉減振器和發電機組成，其基本結構形式如圖2所示。根據集總參數建模方法簡化原則和基本假設[12-13]建立增程器的扭轉動力學總模型，如圖3所示。下面詳細介紹內燃機式增程器各個子系統模型的具體簡化和建立過程。

圖2 內燃機式增程器結構示意圖

圖3 內燃機式增程器總體動力學模型

1.2 發動機動力學模型

根據工作原理和結構組成[12]把慣量大且集中的曲拐、自由端和飛輪作為集中慣量，把慣量小且分散的主軸頸作為無慣量的彈性元件，忽略軸系縱向、橫向振動和整機振動對扭轉振動的影響，假定激勵轉矩和內外部阻尼只作用在或通過等效的方法作用在集中慣量上。據此建立發動機扭轉振動模型，如圖4所示，得到系統扭轉振動微分方程：

圖4 發動機子系統扭轉振動模型

式中：J1為曲軸自由端的等效轉動慣量；J2～J5為曲軸4個曲拐的等效轉動慣量；J6為飛輪和離合器主動盤的轉動慣量；θi為第i個等效慣量的扭轉角位移(i＝1，2，3，4，5，6)；ki為第 i個彈性連接軸扭轉剛度；cri為第i個彈性連接軸軸段內部阻尼系數(i＝1，2，3，4，5)；coi為作用在第 i個等效慣量的外部阻尼系數(i＝2，3，4，5)；M2～M5為作用在各個曲拐的發動機激振轉矩；Tc為離合器傳遞摩擦轉矩。

發動機激勵轉矩主要包括氣缸壓力轉矩和往復運動質量慣性力矩[14]。實際上，由往復運動慣性力所引起的力矩影響較小，往往忽略不計[15]。發動機單缸氣缸壓力轉矩為

式中：D為發動機氣缸直徑；R為曲柄半徑；pg為氣缸壓力；α為相對于上止點的曲柄轉角；β為連桿擺角。

發動機為直列四缸汽油機，點火順序為1-3-4-2。發動機在拖動和額定工況下單缸氣缸壓力隨曲軸轉角的變化如圖5所示。根據第3，4，2缸的氣缸壓力與曲柄轉角關系分別存在π，2π，3π的相位差，可得出發動機各缸壓力及其產生的轉矩[16]。

圖5 拖動及額定工況下發動機單缸氣缸壓力

圖6 曲拐間剛度計算有限元模型

模型中4個曲拐位置的當量轉動慣量可根據曲柄連桿機構進行等效計算得到[17-18]，其他部件的轉動慣量通過在CAD軟件中建立模型并輸入材料參數屬性計算得出，計算結果見表1。彈性連接軸扭轉剛度通過如圖6所示的有限元模型計算。首先建立連接軸的三維模型和有限元模型，利用Abaqus有限元分析軟件在部件的一端添加全約束，另一端施加100N·m的轉矩，仿真計算得到曲拐全約束面與施加轉矩面間的相對扭轉角度為0.000 43rad，進而根據轉矩與扭轉角計算得到扭轉剛度為2.3351×105N·m/rad。發動機阻尼包括曲軸軸段阻尼和外阻尼[19]。軸段阻尼為軸的結構阻尼，表示為coi＝ξoiJiω，外阻尼是由于活塞環、油膜與氣缸接觸作用在活塞上的阻尼，可表示為 cri＝ξriki/ω，其中 ξoi和 ξri為外單位阻尼系數和軸段單位阻尼系數，分別取0.04和0.02[20]。

1.3 離合器動力學模型

單片雙面摩擦片干式離合器集總參數模型見圖7，主要包括主、從動端兩部分。其動力學方程為

式中：J6和J7分別為離合器主動端和從動端轉動慣量；Tf和Tv分別為作用在主動端和從動端的轉矩；θ6和θ7分別為第6個和第7個等效慣量的扭轉角位移。

圖7 離合器子系統模型

當離合器處于滑動狀態時，摩擦轉矩為動摩擦轉矩Tcd；處于接合狀態時為靜摩擦轉矩，包括靜摩擦轉矩 Tc，static和最大靜摩擦轉矩 Tcs，max。 離合器傳遞摩擦轉矩[21]可表示為

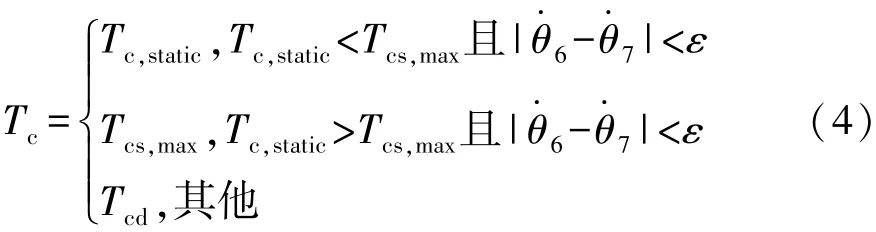
式中ε為離合器主動端與從動端轉速差，根據計算需要設置其為極小值。當主動盤與從動盤轉速差小于極小值ε且靜摩擦轉矩小于最大靜摩擦轉矩時，離合器傳遞的摩擦轉矩為靜摩擦轉矩；當主動盤與從動盤轉速差小于極小值ε且靜摩擦轉矩大于最大靜摩擦轉矩時，離合器傳遞的摩擦轉矩為最大靜摩擦轉矩；當主動盤與從動盤的轉速差大于極小值ε時，即發生相對滑動時，離合器傳遞的摩擦轉矩為動摩擦轉矩 Tcd。 根據牛頓力學定理，Tc，static計算方法[22]為

式中cr7為連接離合器從動盤軸段阻尼內部的阻尼系數。

扭轉減振器集成在離合器內，用于連接從動盤和輸出軸。通過扭轉剛度試驗測得其剛度特性，如圖8所示。扭轉減振器最大轉角為0.296 4rad，剛度特性曲線分為兩段，相對轉角在-θ1～θ1之間為工作區段一，扭轉剛度為348.9N·m/rad；相對轉角在-θ2～-θ1和 θ1～θ2之間為工作區段二，扭轉剛度為509.2N·m/rad。

1.4 發電機模型

由于發電機轉子轉動慣量較大且集中，可忽略發電機轉子本身的扭轉變形，把轉子簡化為集中慣量[12]，電機軸轉動慣量很小，簡化為彈性連接軸，并考慮發電機轉子外部阻尼建立發電機動力學模型為

圖8 扭轉減振器剛度特性

式中：J9為發電機轉子慣量；k8為發電機軸等效扭轉剛度；θ9和θ8分別為發電機轉子和輸入軸前端的扭振角位移；TG為發電機轉矩；cr8為發電機輸入軸軸段阻尼系數，由于很小可忽略[22]；co9為發電機外部阻尼系數。

發電機動力學模型只是發電機模型的一部分，發電機模型還包括最大轉矩電流比控制模塊、弱磁模塊、坐標變換模塊等，其模型框圖如圖9所示，具體建模過程參見文獻[23]和文獻[24]。

各子系統模型參數如表1所示。

1.5 增程器控制系統模型

典型工況下分析增程器扭轉振動特性需要考慮增程器起動、運行、停機和怠速等不同工況下發動機和發電機的轉速、轉矩等的控制，據此本文中所研究的增程器的控制系統主要分為起動、運行和停機3種控制模式，其總體模型框圖和各模式控制流程圖分別如圖10和圖11所示。

圖9 發電機模型框圖

起動控制模式作用于增程器從拖動起動到發動機點火成功的工作過程。當增程器接收到功率需求時，由發電機拖動發動機，發動機在轉速達到800r/min時點火起動，控制系統判斷轉速大于850r/min后，發電機轉矩清零，保持一定的油門開度，若系統判定點火失敗則由發電機重新進行拖動起動，點火成功后由起動控制模式進入運行控制模式。

運行控制模式是發動機和發電機均處于工作狀態，發動機點火成功后進入怠速運行、工況切換、穩定運行階段等的控制方法。采用功率環PI控制調節發動機油門開度進行功率控制，轉速環PI控制對增程器系統進行調速。

表1 各子系統模型參數

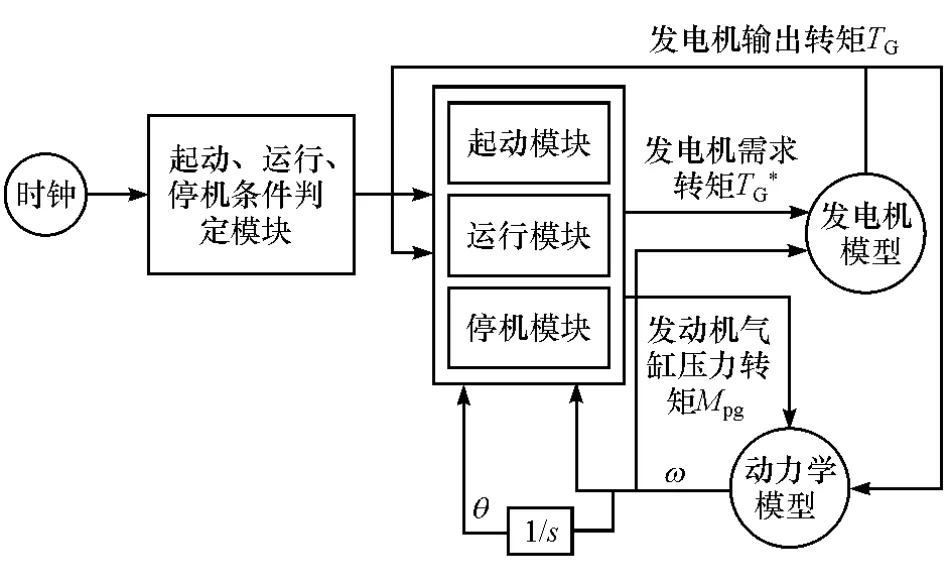
圖10 增程器控制系統模型框圖

停機控制模式下，當增程器接收停機信號后，首先通過運行控制模式使系統在怠速工況下進行冷卻，當冷卻水溫低于閾值時發動機停止點火，發電機轉矩保持恒定直至轉速為零。

2 典型工況工作過程分析

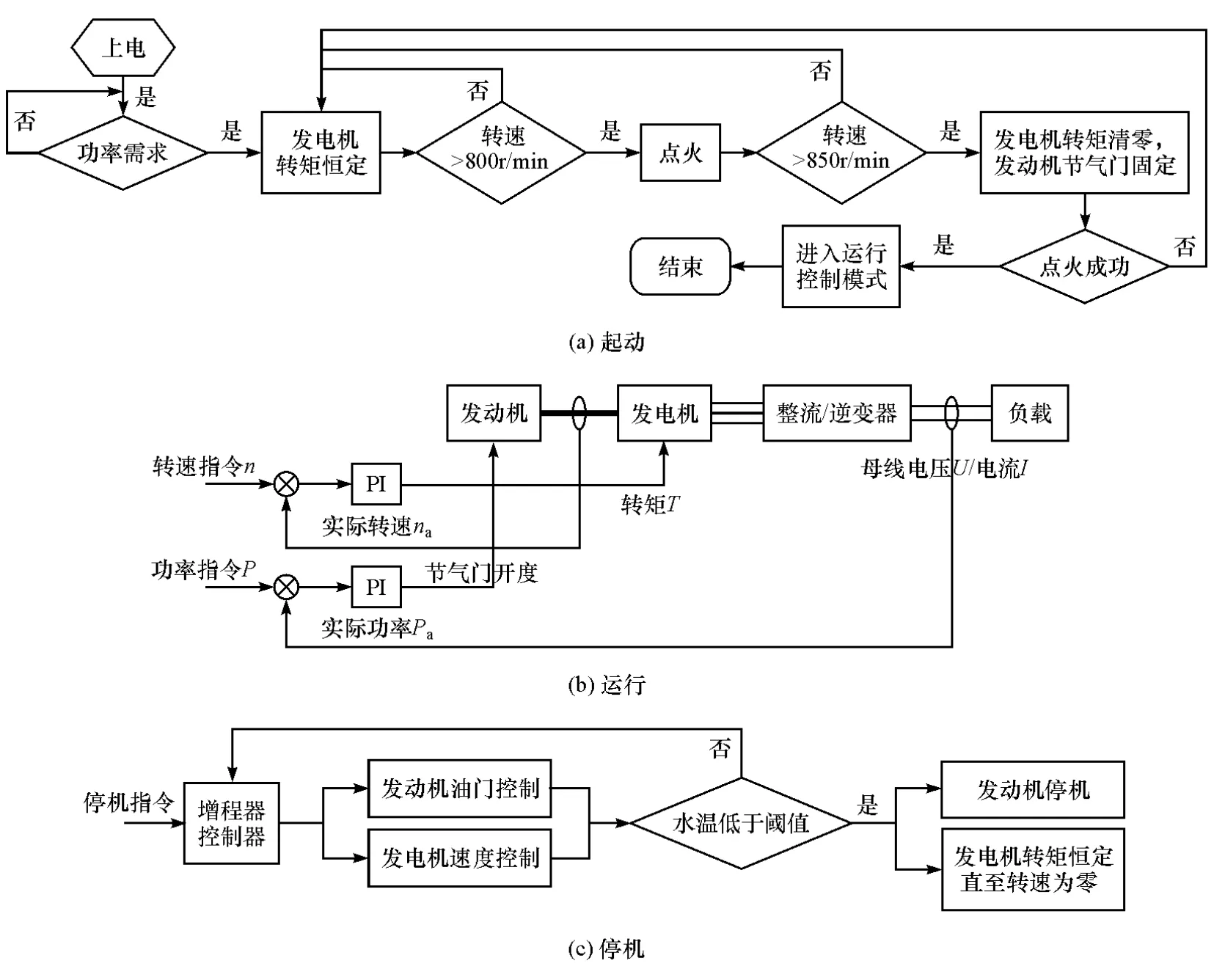
圖11 起動、運行和停機控制模式流程圖

增程器典型工作過程包含7個主要工作階段，如圖12所示。OA為未起動階段；AB為起動階段，系統從停機狀態起動，發電機拖動發動機起動，拖動過程發電機轉矩恒定，達到點火轉速后發動機起動；BC為怠速暖機階段，轉速和功率恒定；CD為從怠速階段切換到穩定運行階段，此時轉速升高，功率增大；DE為穩定運行階段，波浪線表示潛在多個工作點；EF是由穩定運行階段切換到怠速工況，此時轉速降低，功率減小；FG為怠速冷卻階段，轉速和功率恒定；GH為停機階段，此時發動機停機，發電機轉矩恒定，停止后清零。其中穩定運行階段Ⅳ是最常用的工作階段，此時發動機運行在油耗較低的工作點，且有多個工作點可選。根據已測得的發動機的萬有特性曲線和增程器穩態工況下的主要運行工作點，可以發現增程器主要運行在油耗較低的工況，所以大致選取油耗較低的工作范圍，分布范圍為圖13方框所示，在此范圍內選擇穩定運行階段的工作點進行仿真分析。本文中選擇負載轉矩為80 N·m、轉速為3 000r/min作為穩定運行階段工作點。

圖12 增程器典型工作過程

圖13 發動機萬有特性曲線和穩定運行工作點的選擇

3 仿真分析

3.1 響應狀態分析

增程器工作指令分為轉速指令和功率指令，在實際工作中切換過程主要采用階躍變化到目標值，這種方式簡單快速，便于在控制系統中實現。為判斷系統對轉速指令和功率指令的響應情況，對額定工況下增程器實際轉速和發電機功率響應進行時域分析。設置起動階段、穩定運行階段、怠速冷卻階段和停機階段的轉速指令分別為1 300，3 000，1 300r/min和0，發電機的功率響應指令分別為6，28，6kW和0，仿真結果如圖14所示。拖動起動階段①的發動機轉矩為泵氣轉矩，發電機轉矩保持恒定，此階段尚未給出轉速和轉矩指令；當轉速達到800r/min時進入點火階段②，發動機點火起動，發電機轉矩清零，由發動機帶動發電機加速進入怠速暖機階段Ⅱ；怠速暖機階段Ⅱ轉速穩定在1 200r/min左右，發電機功率保持恒定；切換過程Ⅲ，發動機和發電機轉矩迅速變化，轉速快速上升后進入穩定運行階段Ⅳ，此時，發動機轉速和發電機功率都保持恒定；切換過程Ⅴ發動機轉矩迅速減小，系統轉速和發電機功率都逐漸降低，在發電機轉矩作用下發動機減速至目標的怠速冷卻階段Ⅵ，此時，發動機轉速和發電機功率都保持恒定；停機階段Ⅶ，發動機停止點火，系統在發電機轉矩和阻尼作用下減速停機，發電機功率也逐漸降低到零。

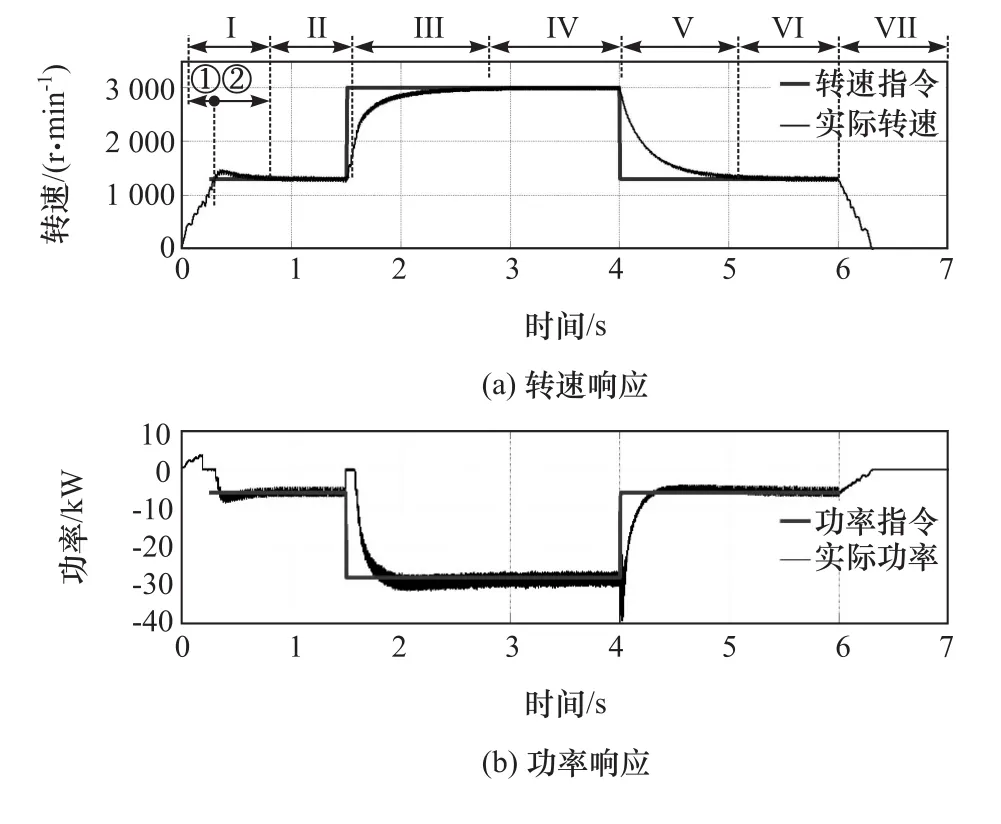
圖14 典型工況下系統轉速和發電機功率響應

由圖14可知，增程器實際轉速和發電機功率總體上能較快地跟隨指令值，系統對工況變化有較好的響應能力。在1.5和4s這兩個工況切換點轉速和功率沒有迅速跟隨，因為典型工況的切換過程是通過轉速和功率PI控制的，存在加速和減速過程，因此實際轉速和發電機功率不能突變到指令值。1.5～1.6s間發電機功率由原來的負值變化為0，主要是因為轉速和功率PI調節的結果，為使系統轉速迅速上升，功率PI控制使發電機功率暫時為零。

3.2 系統激勵轉矩特性分析

典型工況下增程器發動機和發電機轉矩時間歷程和時頻圖分別如圖15和圖16所示。由圖15可以看出，發動機轉矩在穩定運行階段波動最大，怠速暖機和怠速冷卻階段波動次之，起動和停機階段波動最小，主要是因為在不同階段發動機氣缸壓力力矩不同所致。在怠速暖機和怠速冷卻階段主要為轉速的2階、4階和6階成分，在穩定運行階段還增加了8階、10階和12階等較高偶數階成分；由圖16可知，0～0.3s，發電機轉矩先保持恒定，然后降為零，主要是用于拖動發動機起動。6～6.3s發電機轉矩保持恒定值，主要是用來使發動機在恒定轉矩下逐漸停機。在怠速暖機、怠速冷卻和穩定運行階段發電機轉矩波動幅度相近，在起動和停機階段波動較小。發電機轉矩主要成分為轉速的24階和48階高頻成分，同時還存在一定的2階成分。

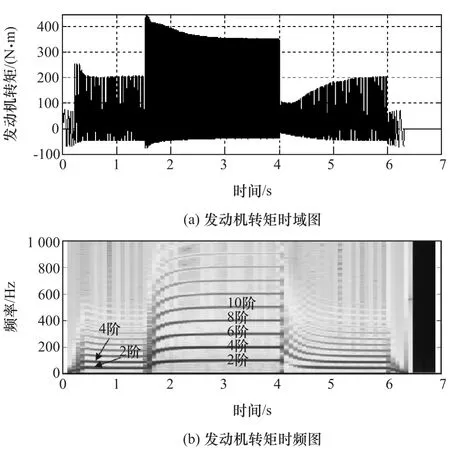
圖15 發動機轉矩時間歷程及其時頻圖

3.3 軸系扭轉振動特性

為全面分析增程器的扭轉振動特性，對增程器

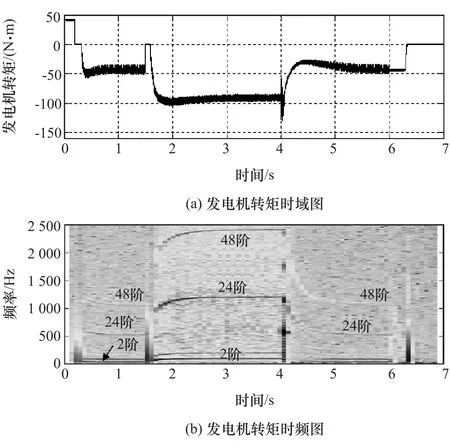
圖16 發電機轉矩時間歷程及其時頻圖

自由端、飛輪和發電機轉子在典型工況下的扭振角加速度的時域和頻域特性進行分析。典型工況下自由端、飛輪和發電機轉子扭振角加速度時間歷程及時頻圖分別如圖17～圖19所示。由圖可知，切換過程中3個工作點的扭振角加速度存在明顯突變，穩定運行階段自由端扭振角加速度最大，飛輪次之，發電機轉子最小。自由端扭振角加速度在怠速階段主要為2階、4階和6階等，且幅值隨階數的增加而減小；在穩定運行階段主要階次依次為10階、8階、6階和4階，由發動機轉矩時頻圖可以得出這些階次主要受發動機激勵的影響。飛輪扭振角加速度主要階次依次為2，4，6階等，與發動機轉矩時頻圖相關度較高，因而主要由發動機激勵引起。發電機轉子扭振角加速度與發電機轉矩時頻圖比較發現，除24階和48階的高階次成分，還多出了2，4，6階低階次成分，說明發電機轉子扭轉振動主要受發電機和電動機轉矩的共同影響。

圖17 自由端扭振角加速度時域及其時頻圖

圖18 飛輪扭振角加速度時域及其時頻圖

圖19 發電機轉子扭振角加速度時域及其時頻圖

圖20 瞬態工作階段功率譜密度分析

為更好反映起動、切換和停機階段瞬態過程振動特性，對振動角加速度進行功率譜密度分析，結果如圖20所示。起動和停機階段自由端、飛輪和發電機轉子都在頻率較低處出現峰值，主要是因為工況變化引起的瞬態振動沖擊和發動機轉矩波動引起的振動，而切換過程Ⅲ和Ⅴ在頻率約480Hz處都出現了峰值，與計算得出的系統2階固有頻率(487.7，487.8和488.7Hz)相近，推測是發生了共振。根據以上分析可以得出，起動和停機階段，軸系存在振幅較大的沖擊振動主要由激勵轉矩突變和激勵轉矩波動引起的；切換階段振幅較大，存在明顯沖擊主要是由激勵轉矩突變和共振引起的。怠速暖機和怠速冷卻階段，系統角加速度波動較大主要由激勵轉矩波動引起；穩定運行階段，系統角加速度大幅波動主要是由系統共振和激勵轉矩波動引起的。

4 結論

針對某商用車用增程器建立了其扭轉振動動力學模型，并在典型工況下分析了模型的工作狀態、激勵轉矩和扭轉振動特性，主要得出以下結論。

(1)利用集總參數法建立的增程器扭轉振動模型能較好模擬增程器實際運行中出現的扭振現象。

(2)典型工況下，增程器的扭轉振動不僅與發動機的激勵轉矩波動和突變有關，且受到發電機的電磁轉矩波動和突變及系統共振影響。

(3)自由端的扭轉振動在增程器轉速較低時受轉矩影響較大，在轉速較高時受轉速影響較大。