不同類型降雨條件下含裂隙土質邊坡滲流特性分析
魏凌傲 王正君 郜 迪
(黑龍江大學 水利電力學院, 哈爾濱 150080)
降雨對邊坡的穩定性影響巨大,主要體現在:降雨抬高了地下水位,使得土體的有效應力減小[1-2];降雨使得邊坡內部土體的強度減小,土體更容易發生剪切滑動[3-4].同時,也有研究表明,不同類型降雨對邊坡的滲流特性影響巨大:如郁舒陽[5]對不同類型降雨下的不同Fredlund&Xing參數土體的滲流特性進行了研究;王寧偉[6]對在不同類型降雨條件下的邊坡入滲深度以及體積含水量變化規律進行了探討.
在自然的風化作用以及草本植物根系作用下,邊坡土體表層難免會產生一定角度,一定深度的裂隙[7],這些裂隙的滲透性較原狀土更高,可以極大的改變降雨過程中的雨水入滲規律,已有學者對其進行了相應的研究:如袁俊平[8-9]系統的對降雨條件下膨脹土裂隙的分布位置,各向異性程度,裂隙角度以及裂隙深度的滲流特性進行了分析;王培清[10]對裂隙性紅黏土降雨條件下的邊坡滲透穩定性進行了研究;闕云[11]對降雨條件下的裂隙性粘土邊坡的滲流特性進行了模擬討論,但是縱觀國內外文獻,不同降雨類型下含裂隙邊坡滲流特性卻鮮有報道,相應的規律還沒有一個清晰的認識.
本文以某含裂隙土質邊坡模型為例,選取平均型,前鋒型,中鋒型以及后峰型4種降雨類型,利用有限元分析軟件Geo-slope中的Seep/w與Slope/w模塊,研究了不同類型降雨條件下裂隙不同深度,不同角度以及裂隙不同滲透比的滲流特性,所得結果為進一步認識不同類型降雨下含裂隙邊坡的滲流特性以及治理提供了一定的參考.
1 計算理論與模型
1.1 計算理論
非飽和滲流的控制方程形式為:
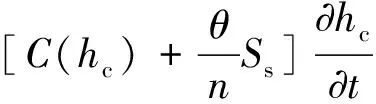
(1)
式中,kr為相對透水率;kij為飽和滲透張量;hc為壓力水頭;Q為源匯;C(hc)為容水度;θ為壓力水頭函數;n為孔隙率;Ss為單位貯水量.
土水特征曲線是描述土體滲透系數或者體積含水量與基質吸力的關系,采用VG模型進行估算[12]:
(2)
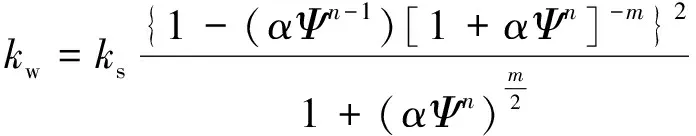
(3)
式中,θw為土體的含水率;θs為土體的飽和含水率;θr為土體的殘余含水率;ks為土體的飽和滲透系數;kw為土體的瞬時滲透系數,即相應基質吸力下對應的滲透系數;Ψ為土體的基質吸力;a,m,n為公式的擬合參數,其中n可以表示為:
n=1/(1-m)
(4)
1.2 計算模型及邊界條件
模型取自文獻[9],邊坡的坡高為10 m,坡比為1∶2,裂隙位置設置在坡頂,如圖1所示.在裂隙位置設置一監測面來實時監測不同類型降雨過程中的孔壓以及體積含水量的變化規律.模型網格剖分圖如圖2所示,在坡頂裂隙處網格適當加密,全局一共剖分為755個單元,801個節點.
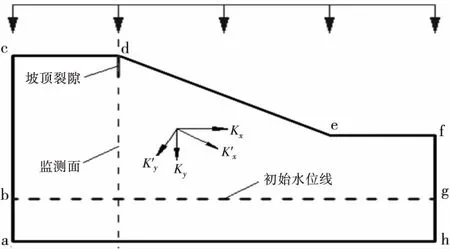
圖1 計算模型
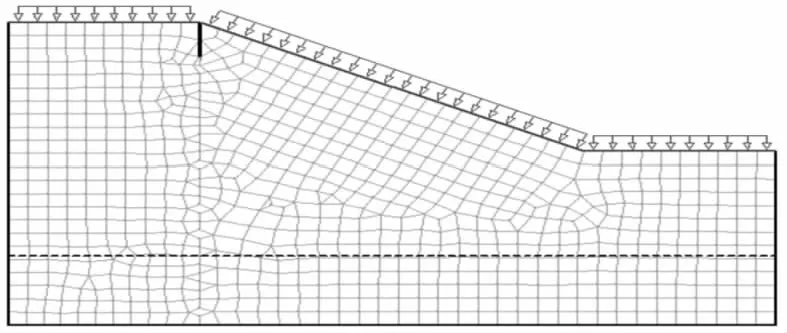
圖2 模型網格剖分圖
模型初始條件取如圖1所示的初始水位下的滲流場作為整個計算工況的初始滲流場,邊界條件如下:ab,gh為零流量邊界;ah,bc,fg為不透水邊界;cdef為降雨入滲邊界.
裂隙模擬方法較多,本文取文獻[8]的模擬思路,即將裂隙土部分視為一種各向異性材料,而在計算過程中,裂隙的數學描述可以用裂隙長度h,即裂隙沿著深度方向的長度大小;裂隙面與豎直方向的夾角α,以及順裂隙方向與垂直裂隙方向的滲透系數比值μ來刻畫.其中,裂隙單元的局部坐標與整體坐標的轉換關系如下式所示:
(5)
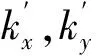
2 計算方案及材料參數
降雨采用4種不同類型降雨,平均型,前鋒型,中鋒型以及后峰型降雨,降雨過程曲線如圖3所示,降雨總量為0.14 m,降雨天數為7 d,同時考慮停雨5 d的情況,總計算時間為12 d.
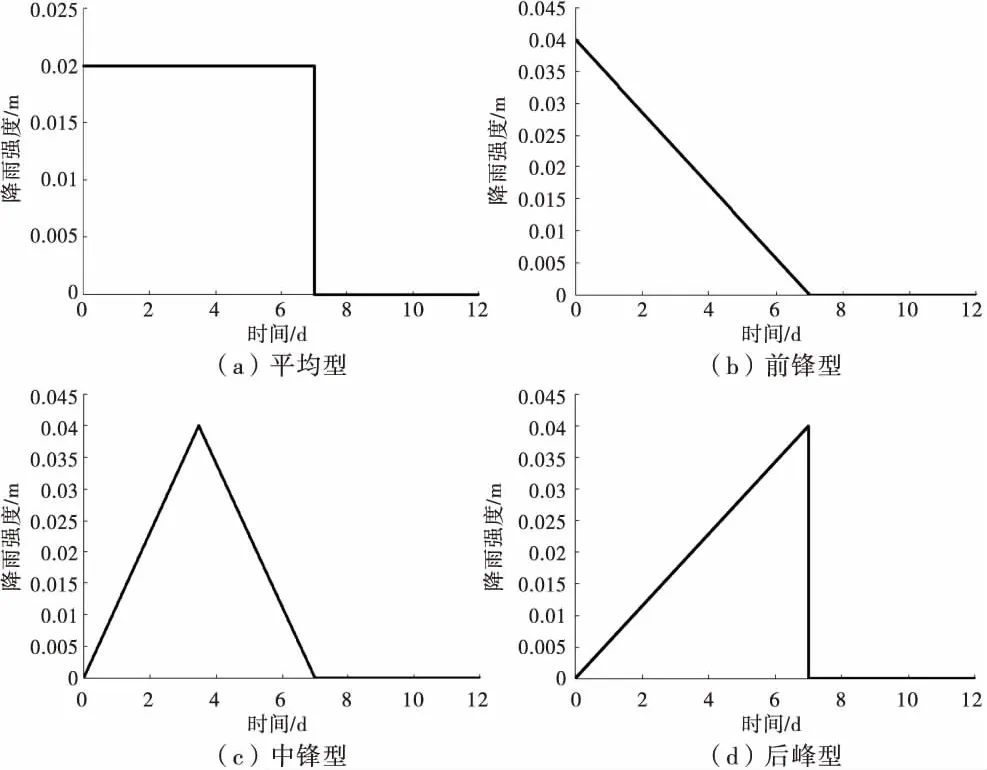
圖3 降雨過程曲線
計算內容考慮裂隙不同深度,不同裂隙方位角α以及不同的滲透系數比值μ(即順裂隙方向與垂直裂隙方向滲透系數比值)在不同類型降雨條件下的滲流特性,具體計算工況見表1.
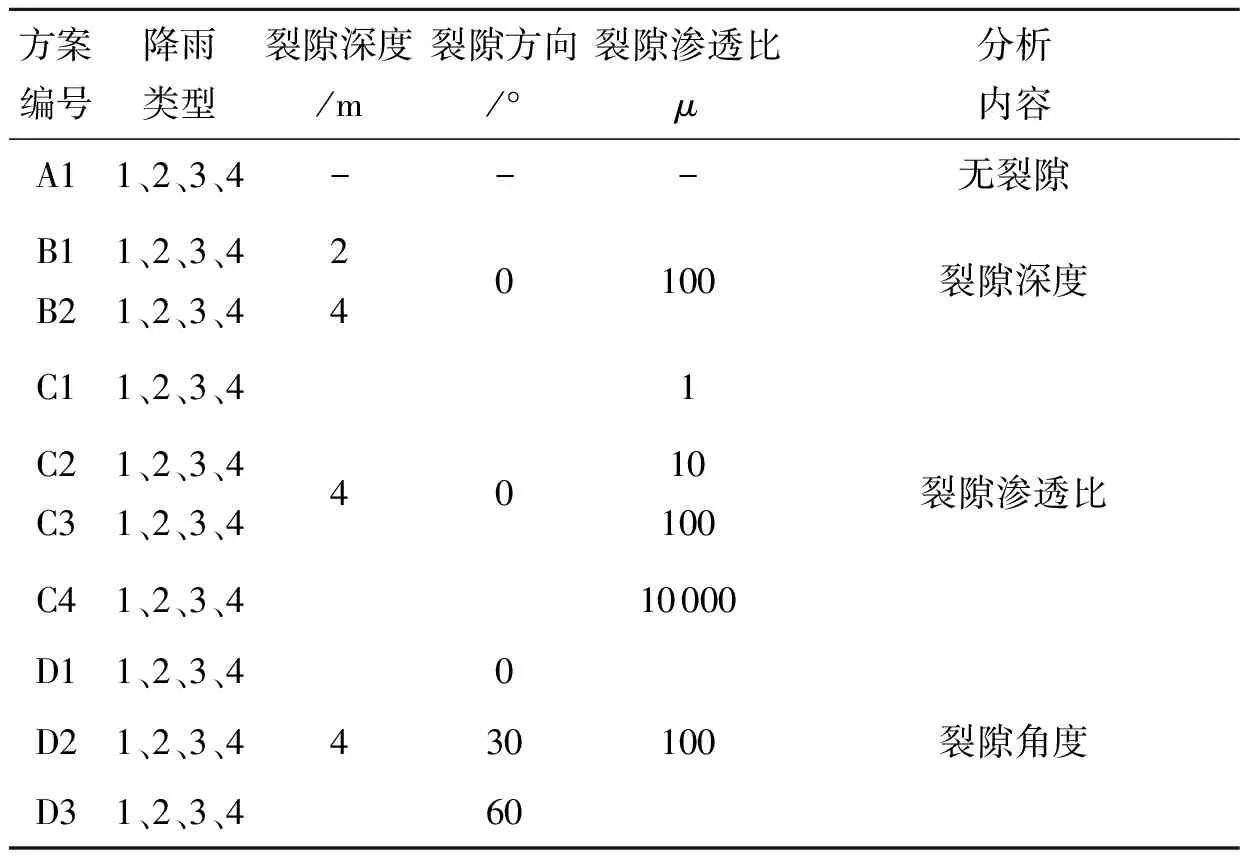
表1 計算工況
注:降雨類型1、2、3、4分別代表平均型降雨,前鋒型降雨,中鋒型降雨以及后峰型降雨.
土體滲流參數依據文獻[9]確定,a=166.7 kPa,n=1.567,θs=0.495,θr=0.262,原狀土飽和滲透系數ksat=2.83×10-4m/d,垂直裂隙方向飽和滲透系數ksatx=2.83×10-2m/d,根據公式(2)~(4),可以得出原狀土與裂隙土的土水特征曲線如圖4所示.
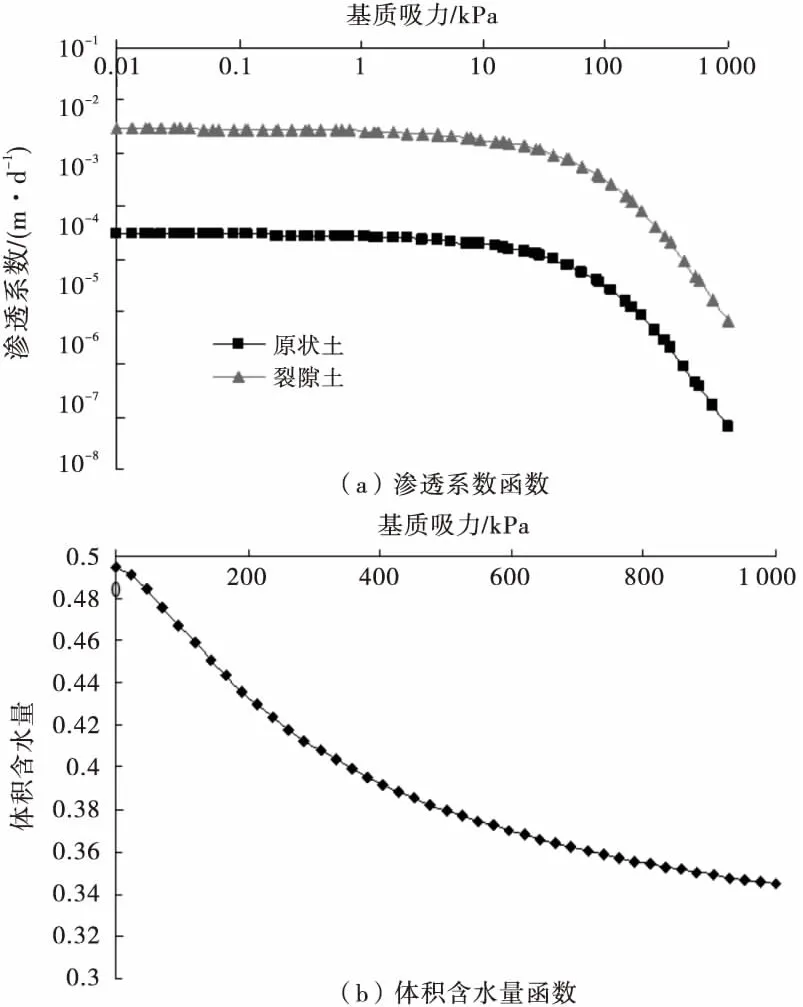
圖4 土水特征曲線
3 計算結果分析
3.1 不同裂隙深度滲流特性
邊坡無裂隙,坡頂裂隙深2 m以及坡頂裂隙深4 m情況下的監測面體積含水量變化如圖5所示.
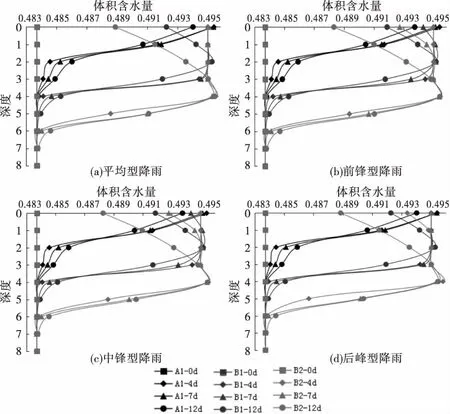
圖5 工況A、B體積含水量變化
由圖可見,不同降雨類型下,不同裂隙深度下監測面的體積含水量變化呈現不一樣的規律,從整體上看,不同類型降雨工況下體積含水量變化存在一個“極限深度”,即濕潤鋒的最大影響深度,無裂隙工況下濕潤鋒影響的最大深度為4 m,裂隙為2 m工況下的濕潤鋒最大影響深度為6 m,而裂隙為4 m工況下的濕潤鋒最大影響深度為7 m,并且不同類型降雨對濕潤鋒的最大影響深度沒有明顯的影響;裂隙深度越深,在停雨后的土體表面體積含水量消散的越快,以圖5(a)為例,無裂隙工況停雨后孔壓消散最慢,在第12 d土體表層體積含水量為0.494,裂隙為2 m工況下的第12 d土體表層體積含水量為0.492,而裂隙為4 m工況下的第12 d土體表層體積含水量為0.489,因此,土體不含裂隙情況下體積含水量變化規律是隨著深度逐漸遞減,直到達到“極限深度”后保持不變,而含裂隙情況下體積含水量變化規律是隨著深度先增大后減小,并且拐點約為裂隙深度處,最后減小到“極限深度”后保持不變;不同降雨類型對體積含水量變化規律影響不大,對每個瞬時的孔壓數值大小稍有影響,以裂隙深度為4 m工況下不同類型降雨在第12 d的孔壓為例,平均型降雨下土體表層孔壓為0.489,前鋒型降雨土體表層孔壓為0.488,中鋒型降雨土體表層孔壓為0.488,而后峰型降雨土體表層孔壓為0.489.相應的孔壓變化規律如圖6所示.
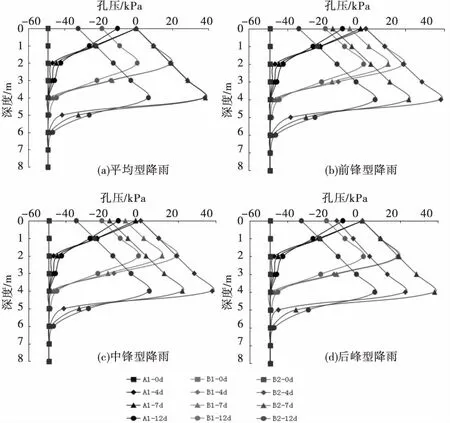
圖6 工況A、B孔壓變化
可見不同降雨條件下不同深度裂隙土體內部孔壓變化規律較為一致,無裂隙土體在降雨過程中孔壓呈現隨深度逐漸減小的趨勢,而含裂隙土體在降雨條件下孔壓隨時間呈現先增大后減小,最后保持不變的規律,且在裂隙底部孔壓達到最大值,同時,裂隙深度越大,裂隙底部的最大孔壓值也越大,以圖6(a)平均型降雨為例,裂隙為2 m工況下所達到的最大孔壓為20 kPa,而裂隙為4 m工況下所達到的最大孔壓則為40 kPa,可見降雨過程中的最大孔壓與裂隙深度呈正相關,縱向來看,不同類型的降雨只是影響了相應孔壓達到最大的時間,對孔壓的分布規律則影響較小.
3.2 不同裂隙滲透比的滲流特性
裂隙滲透比為1,10,100,10 000下的土體內部體積含水量變化規律如圖7所示.
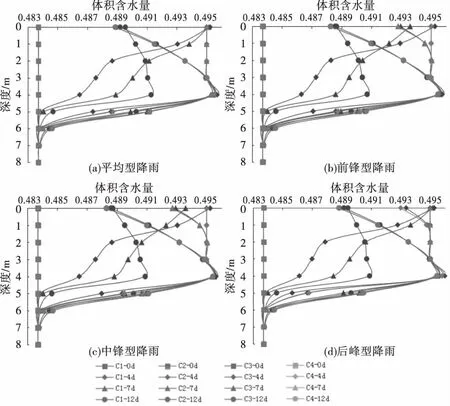
圖7 工況C體積含水量變化
不同類型降雨條件下,不同滲透比呈現出明顯的規律:即滲透比大于10體積含水量變化規律一致,而滲透比為1有明顯的孔壓滯后性,即土體表層的孔壓消散較滲透比大的工況要慢,究其原因,是因為土體滲透比較大的情況下,垂直裂隙方向的滲透率就等于降雨的入滲強度,所以當滲透比大于10的工況下體積含水量變化規律趨于一致,而當滲透比較小時,降雨強度大于入滲強度,有一部分水被滯留于土體表層,即表現出體積含水量的消散“滯后”現象.不同類型降雨影響了不同時刻的體積含水量變化規律,以工況C1為例,平均型降雨下7 d土體表層一直保持為飽和狀態,第12 d土體表層體積含水量減至0.489;前鋒型降雨下在第7 d土體表層體積含水量就開始下降至0.4924,在第12 d時體積含水量降至0.487 8;中鋒型降雨在第7 d土體表層體積含水量也有所下降,在第12 d降至0.4878;后峰型降雨條件下第7 d土體表面仍為飽和狀態,而第12 d降至0.489 2.相應的孔壓變化如圖8所示.
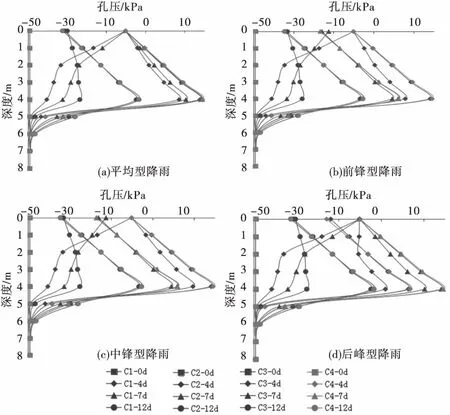
圖8 工況C孔壓變化
孔壓變化與體積含水量較為相似,即滲透比為1與滲透比大于10的孔壓變化差異較大,這也是由于土體滲透比較大的情況下,垂直裂隙方向的滲透率就等于降雨的入滲強度,所以當滲透比大于10的工況下孔壓變化規律趨于一致,而當滲透比較小時,降雨強度大于入滲強度,有一部分水被滯留于土體表層,即表現出孔壓“滯后”現象;滲透比越大,土體內部達到的最大孔壓也越大,同時,滲透比大于10孔壓變化較為一致.
3.3 不同裂隙方位角滲流特性
裂隙方位角為0°,30°,60°情況下土體內部體積含水量變化規律如圖9所示.
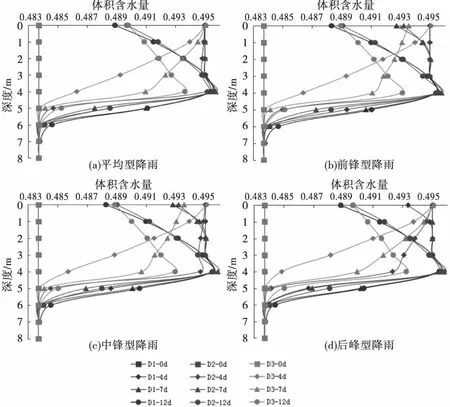
圖9 工況D體積含水量變化
由圖可見,在不同類型降雨條件下,裂隙方位角為0°與30°時體積含水量變化規律較為一致,而裂隙角度為60°情況下與前兩種工況的差異性較大,這是因為裂隙方位角為0°與30°時,裂隙豎向滲透系數較大,雨水入滲較為容易,即兩者體積含水量變化規律較為一致,而裂隙角度為60°時,裂隙接近于水平,而垂直裂隙方向的滲透系數較順裂隙方向的滲透系數要小兩個數量級,即雨水較難入滲,所以裂隙角度為60°時的體積含水量變化要滯后于0°與30°的體積含水量變化.不同類型降雨影響了不同時刻土體一定深度內的體積含水量變化,以工況D1為例,平均型降雨下7 d土體表層一直保持為飽和狀態,第12 d土體表層體積含水量減至0.489;前鋒型降雨下在第7 d土體表層體積含水量就開始下降至0.493,在第12 d時體積含水量降至0.488;中鋒型降雨在第7 d土體表層體積含水量也有所下降,在第12 d降至0.488;后峰型降雨條件下第7 d體積含水量降至0.493 2,而第12 d降至0.487 9.相應的孔壓變化規律如圖10所示.
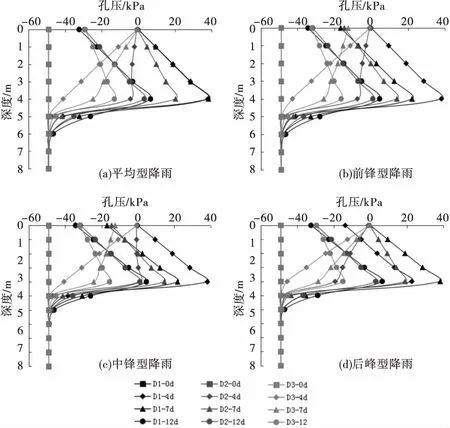
圖10 工況D孔壓變化
孔壓變化與體積含水量變化有較好的吻合性,即裂隙傾角為0°與30°情況較為接近,而60°情況差異較大,這也是由于裂隙方位角為0°與30°時,裂隙豎向滲透系數較大,雨水入滲較為容易,即孔壓變化較為一致,而當裂隙角度為60°時,裂隙接近于水平,而垂直裂隙方向的滲透系數較順裂隙方向的滲透系數要小兩個數量級,即雨水較難入滲,孔壓變化較為緩慢,但是裂隙角度的差異性也比較明顯,即隨著裂隙角度的增大,土體表層孔壓的消散速度也越來越慢,并且最大孔壓也越來越小.不同類型的降雨也只是影響了相應孔壓達到最大的時間,對孔壓的分布規律則影響較小.
3.4 實例分析
文獻[13]中介紹了南水北調南陽現場試驗段膨脹土邊坡滑坡破壞實例.現場調查結果表明,該現場試驗段膨脹土裂隙極其發育,其中長大裂隙有至少2組以上優勢方向,裂隙區域土體發現呈明顯各向異性.裂隙傾向統計結果顯示,主裂隙傾向與坡面幾乎平行,即順裂隙方向與豎向夾角約為50°~75°.現場觀測表明,降雨后吸濕區范圍約為0.5 m,吸濕區內土體含水率增大約為16.5%,表明這種裂隙傾向條件下,降雨入滲的影響范圍和影響程度均較小.這與本文計算結果相吻合,即順裂隙方向與豎直方向夾角較大時,裂隙各向異性對邊坡的滲流影響較小.
4 結 論
1)不同裂隙深度土體內部含水量與孔壓均存在一個最大影響深度,裂隙深度越大,影響深度越大.無裂隙土體體積含水量與孔壓在降雨條件下隨深度呈現先減小后不變的規律,而含裂隙土體體積含水量與孔壓在降雨條件下隨深度呈現先增大后減小最后保持不變.
2)土體滲透比大于10時體積含水量與孔壓差異較小,而滲透比小于10的情況與大于10的情況差異較大,同時滲透比越大,土體表層含水量消散速度越快.
3)裂隙角度越小,土體內部含水量與孔壓上升越快,同時,裂隙角度為0°與30°情況體積含水量與孔壓變化規律較為接近,而裂隙角度為60°時體積含水量與孔壓變化與前者差異較大.
4)不同類型降雨影響了含裂隙土體內部孔壓與體積含水量的瞬時數值變化大小,對于孔壓以及體積含水量的變化規律影響較小.

