橋梁結構非平穩隨機抗震分析

但慶文 張傳勇 劉章軍

(三峽大學 土木與建筑學院， 湖北 宜昌 443002)

橋梁結構是人類社會發展的重要基礎設施，隨著科技進步和建造材料的開發，橋梁結構日益朝著大跨高墩的方向發展，越來越多的大跨高墩剛構橋、斜拉橋以及懸索橋建成服役，這些橋梁結構在強震作用下都不可避免地會產生非線性響應．對大跨度橋梁隨機地震響應分析和抗震可靠度評價是橋梁結構設計的重要內容，而地震動時程的模擬是基于動力時程分析的橋梁結構抗震研究所面臨的首要課題[1]．由于強度非平穩地震動模型的物理意義明確、使用簡便，人們大多采用其作為地震動輸入模型[2-4]．然而，地震動的頻率非平穩對結構的非線性動力作用同樣重要，需要更全面真實地反映結構的動力響應，因此，近年來合理考慮地震動的全非平穩特性成為地震動建模的重點和熱點．曾珂等人發展了一類地震動時變模型，該模型較好的考慮了頻率非平穩性[5]；張翠然等人在Priestley[2]演變譜理論的基礎上通過擬合目標演變譜構造了強度-頻率非平穩地震動模型；同樣地，胡燦陽等人在此演變譜理論基礎上，通過引入了強度-頻率雙調制函數模型，建立了一類雙調制地震動過程模型[6]；劉章軍等人從工程應用的角度出發，通過構造與現行水工抗震規范相結合的強度-頻率調制函數，建立了一類強度-頻率演變功率譜模型[7]，其優點在于參數可以方便地由抗震規范確定，且適用于公路工程抗震規范．

本文將借鑒文獻[7]中構造廣義演變功率譜的思路，結合最新的《公路工程抗震規范》(JTG B02-2013)[8]，發展一類與最新橋梁抗震規范相結合的改進Kanai-Tajimi功率譜，同時考慮地震動的強度非平穩特性和頻率非平穩特性，建立非平穩地震動過程的強度-頻率演變功率譜模型．然后，結合強度-頻率演變功率譜密度模型和非平穩地震動過程的譜表示-隨機函數降維法[9-11]，生成610條與公路工程抗震規范相對應的地震波樣本集合，并對模擬結果的二階統計量、演變功率譜密度函數和平均反應譜進行了分析，以驗證本文方法的有效性．最后，將生成的概率完備的代表性時程集合和概率密度演化方法[12-13]結合，對范和港大橋的隨機地震動響應及抗震可靠度進行了精細化的分析．

1 非平穩過程模擬的譜表示-隨機函數方法

根據非平穩地震動過程模擬的譜表示方法，對于零均值、雙邊演變功率譜密度函數為SX(t，ω)的非平穩地震動過程X(t)(一維單變量隨機過程)可近似表示為[9]：

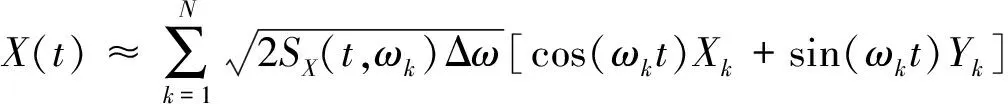
(1)

式中，SX(t，ω)滿足SX(t，ω0)=SX(t，0)=0；Δω=ωu/N為頻率步長，ωu為上截斷頻率，N為頻率截斷項數，ωk=kΔω．Xk和Yk(k=1，2，…，N)為一組標準正交的隨機變量，其滿足如下基本條件[9]：

E[Xk]=E[Yk]=0，E[XkYl]=0，

E[XkXl]=E[YkYl]=δkl

(2)

式中，E[·]為數學期望，δkl為Kronecker記號．

在式(1)中，當N取有限項時，X(t)的均方相對誤差為[9]：

(3)

式中，T為地震加速度過程的持時．

在此模擬方法中，其核心在于確定式(1)中功率譜密度函數SX(t，ω)的表達式和正交隨機變量{Xk，Yk}的表達式，利用隨機函數的降維思想[11]，式(1)中的{Xk，Yk}可方便的確定為：

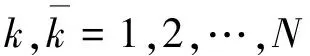
(4)

其中，基本隨機變量Θ在區間(-π，π)上均勻分布．

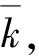
2 時-頻非平穩地震動模型

在傳統的結構非線性地震分析中，一般采用僅考慮強度非平穩的地震動模型，然而頻率非平穩對結構的非線性分析同樣有著重要的影響．為此，本文在平穩地震動過程的Kanai-Tajimi功率譜[14-15]基礎上，采用文獻[7]中的方法構造了一類時-頻非平穩地震動模型．

首先，根據文獻[14-15]，Kanai-Tajimi的廣義功率譜可定義如下：

(5)

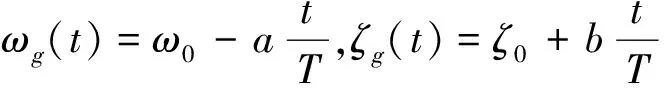
(6)

式中，ωg(t)和ω0分別為場地土的時變頻率和卓越圓頻率；ζg(t)和ζ0分別為場地土的時變阻尼比和阻尼比．參數ω0、ζ0和a、b可根據場地類別來確定；S0(t)為譜強度因子，其表達式為：

(7)

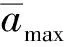
其次，選取強度調制函數，本文選取Shinozuka提出的一種強度調制函數[16]：

(8)

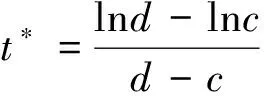
(9)

式中，t*為地震動峰值到達時間的均值，參數c和d可根據場地類別來確定，且參數c和d反映了地震動過程的強度非平穩性．

最后，根據上述Kanai-Tajimi的廣義功率譜模型和強度調制函數，可以給出如下修正的演變功率譜模型：

SX(t，ω)=|f(t)|2S(t，ω)

(10)

式中，SX(t，ω)為演變功率譜密度函數．

圖1為采用本文方法生成的時-頻演變功率譜密度函數圖，從圖中可以看出在頻域和時域內均表現出明顯的非平穩特性．

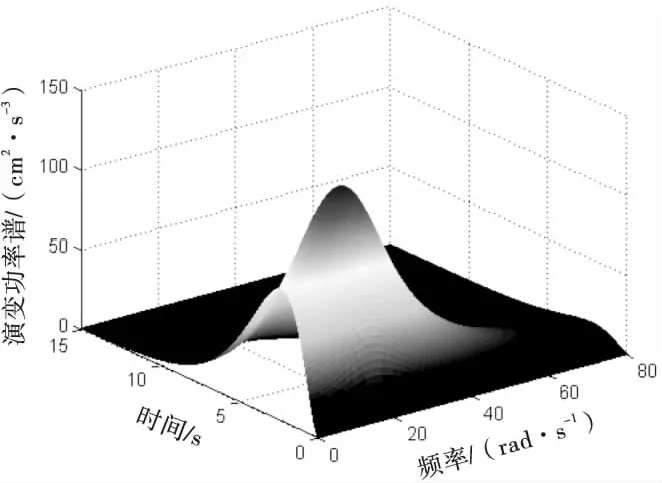
圖1 時-頻演變功率譜密度函數

3 非平穩地震動過程的模擬與驗證

為了生成非平穩地震動代表性時程樣本集合，首先需要對基本隨機變量Θ選取代表性點集，本文對基本隨機變量在區間(-π，π)上選取610個均勻散布的代表性點，同時計算每一個代表性點的賦得概率為1/610．然后，將選取的每一個代表性點代入式(4)中，并完成一一映射，便可得到標準正交隨機變量{Xk，Yk}的代表性集合．最后，將正交隨機變量{Xk，Yk}帶入到非平穩地震動隨機過程的譜表示-隨機函數模擬公式(1)中便可生成非平穩地震動過程的代表性時程．

表1 演變功率譜模型參數

圖2為采用本文方法生成的非平穩地震動過程代表性時程，從圖中可知，代表性樣本具備地震動時程的典型特征，且強震階段一般出現在1/6～1/3持時范圍內；圖3為生成的610條加速度時程的平均傅里葉幅值譜，其反映了地震動能量在頻域中的分布，從圖中可以看出，不同頻率諧波振動所攜帶的能量主要分布在0～15 Hz范圍內．

圖4為采用本文方法模擬的610條地震動加速度時程集合的均值及標準差與目標均值及標準差的比較圖，從圖中可知，模擬值與目標值十分接近，集合均值和集合標準差均在目標均值和目標標準差的上下波動，總體上與目標值的相對誤差均在5%以內．對應地，圖5為采用本文方法生成610條地震動加速度時程集合的估計反應譜與規范反應譜的比較，從圖中可知，模擬值與三段式的規范反應譜擬合很好．上述對比分析說明了利用本文方法生成的地震動加速度時程具有較高的精度，可以用于工程結構抗震分析．

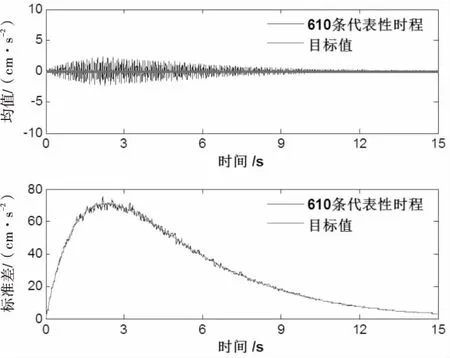
圖4 610條代表性時程二階統計值與目標值比較

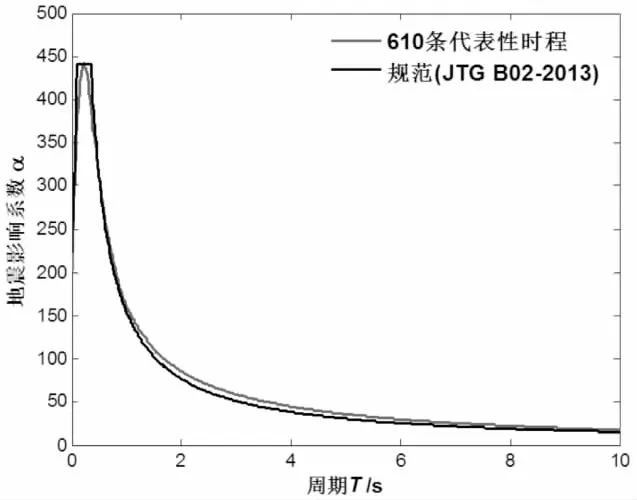
圖5 平均反應譜與規范反應譜的比較

4 范和港跨海斜拉橋抗震分析

由于非平穩地震動隨機過程的譜表示-隨機函數方法生成的地震動加速度時程具有給定的概率信息，且所有的代表性時程構成一個完備的概率集，因而可結合概率密度演化理論對范和港跨海大橋的隨機地震響應及抗震可靠度進行精細化的分析．

范和港跨海大橋的基本參數如下[17]，橋梁跨徑(52.5+99.5+300+99.5+52.5)=604 m，橋面寬26.9 m，采用雙塔單索，塔高28.31 m．主梁采用C55混凝土，截面形式為單箱三室三角箱型，橫隔梁間距為6 m，箱梁底板厚度為25 cm，頂板為27 cm．索塔為獨柱塔型，順橋和橫橋向分別寬6.9 m和3.4 m，順橋向1.5 m，橫橋向壁厚0.8 m至1.1 m，索塔采用C60混凝土．主塔與主墩剛接，主墩為圓端形截面，長端沿順橋向為13.8 m至15 m，短端沿縱橋向為5.8 m至7 m，壁厚1 m至2 m．全橋設23對一共184根斜拉索，采用8種規格拉索，從PES(FD)7-109到PES(FD)7-211，拉索最小傾角約為24度，梁上索距為6 m，橫向2.2 m，塔上豎向索距為1.6 m，橫向為0.8 m．采用有限元軟件Midas Civil對范和港斜拉橋進行有限元建模，如圖6所示．

圖6 范和港大橋有限元模型

采用多重Ritz向量法對橋梁結構進行模態分析以獲取橋梁結構的自振頻率和各階振型，限于篇幅，僅列出部分模態，見表2．

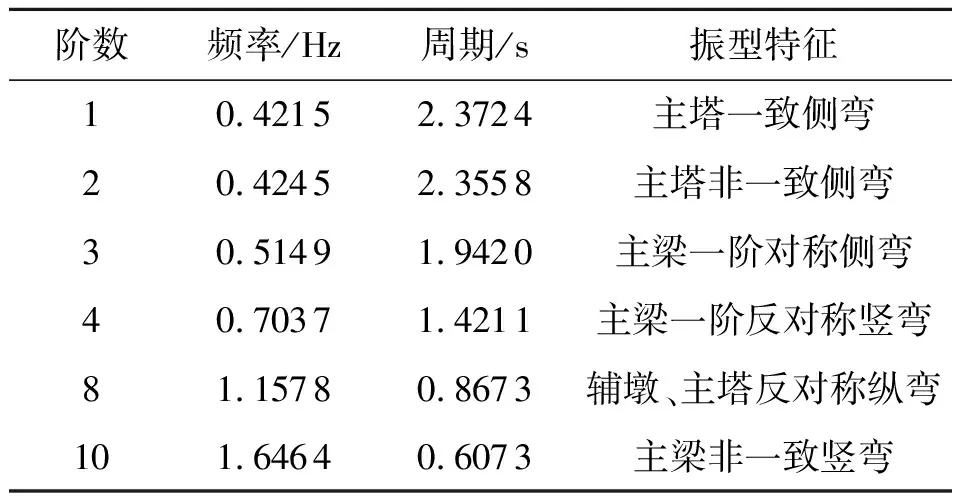
表2 結構部分動力特性

從表中可知：該斜拉橋結構的基頻為0.421 5 Hz，對應的振型為主塔一致側彎，這是因為索塔、主梁、主墩采用了固結形式，有很大的整體剛度；且前三階模態的振型均表現為主塔側彎，說明橋塔的橫向剛度很小；結構的頻譜較為密集，振型分布均勻，尤其高階振型表現為明顯的相互耦合作用．

值得說明的是，式(1)所定義的譜表示模擬公式僅適用于一維單變量隨機過程，其模擬結果只能獲得單點地震動輸入，同時為簡化計算，本文僅考慮一致激勵下的橋梁結構抗震分析，不考慮地震動的多維相關性以及空間變化特性．將采用本文方法生成的610條代表性時程輸入到結構有限元模型中進行確定性的動力時程分析，并結合概率密度演化方法，考慮縱向+橫向和縱向+豎向兩種地震輸入方式，對范和港跨海大橋的非線性地震響應及抗震可靠度進行精細化的分析．方向組合采用SRSS方法，其中水平向地震加速度峰值為0.2g，豎向地震加速度峰值取水平向的0.6倍．限于篇幅，本文僅給出縱向+橫向地震輸入方式下主墩墩底彎矩響應的二階統計量和典型時刻的概率信息，如圖7所示，從圖中可以看出，橋梁結構在地震作用下產生強烈的非平穩響應，且主墩墩底彎矩不同時刻的典型概率密度曲線表現出明顯的隨機性特點．

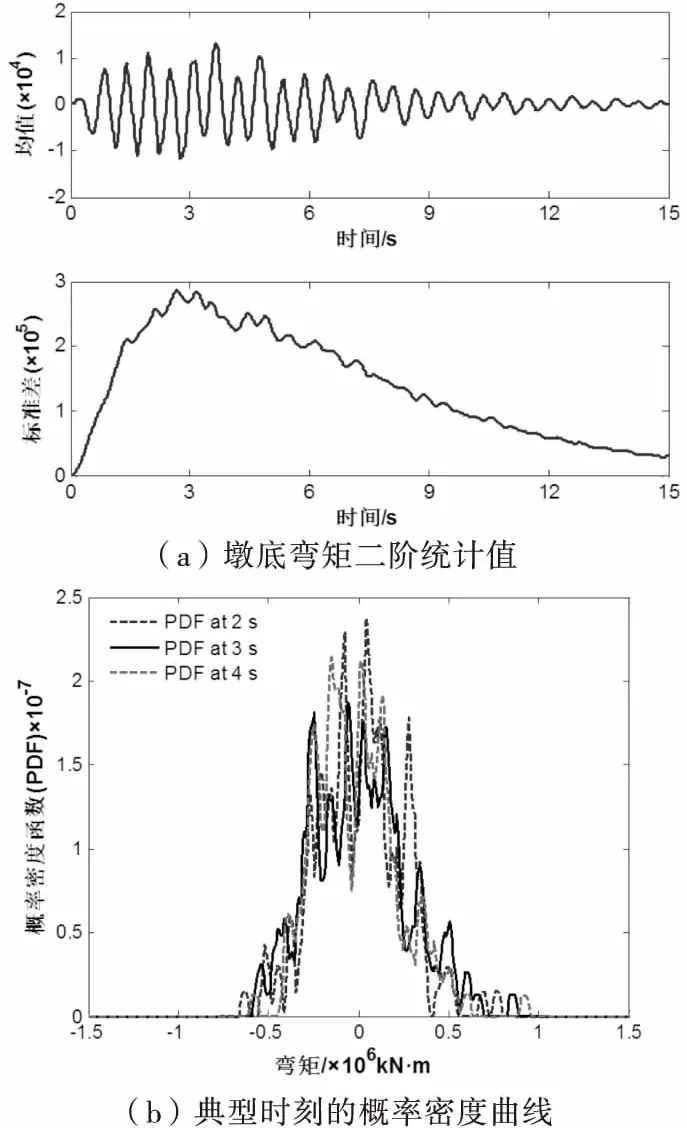
圖7 結構地震反應的概率信息

在上述橋梁結構非平穩地震動響應分析的基礎上，結合等價極值事件的思想[12]，分別取主墩墩底的軸力和彎矩作為可靠度評價指標，對橋梁結構抗震可靠度進行定量的評價．根據大量的震害資料，分別選取可靠度閾值為1.8×104kN和1.0×106kN·m．圖8為縱向+橫向和縱向+豎向地震輸入方式下的橋梁抗震可靠度計算結果，從圖中可以看出，當采用軸力作為可靠度指標時，縱向+橫向和縱向+豎向地震輸入方式下的可靠度分別為100%和65%；當采用墩底彎矩作為可靠度指標時，兩種地震輸入方式下的可靠度曲線幾乎重合，且抗震可靠度均為100%，這說明橫向地震激勵和豎向地震激勵對主墩墩底彎矩的影響是一致的．對比圖8(a)和圖8(b)可以發現，對于同一失效閾值，軸力在縱向+豎向地震輸入方式下的可靠度遠小于縱向+橫向地震輸入的抗震可靠度，這說明豎向地震激勵對墩底軸力的可靠度有較大的影響，其抗震可靠度明顯不滿足，因此在橋梁結構抗震設計中需重點考慮豎向地震激勵對主墩墩底軸力的影響．

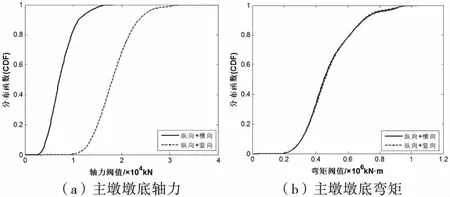
圖8 結構抗震可靠度

5 結 論

本文在平穩地震動過程的Kanai-Tajimi功率譜基礎上，建議了一類時-頻非平穩地震動演變功率譜模型，結合《公路工程抗震規范》(JTG B02-2013)和非平穩過程模擬的譜表示-隨機函數降維方法，生成了與規范反應譜相一致的地震動加速度代表性時程集合．利用 有限元軟件建立斜拉橋有限元模型，對橋梁非平穩地震響應進行了概率密度演化分析．在此基礎上，結合等價極值事件的思想，分別選用主墩墩底軸力和彎矩作為可靠度評價指標，對橋梁結構抗震可靠度進行了精細化的分析．研究結果表明，地震動隨機過程的時-頻非平穩演變功率譜模型能夠充分體現強度和頻率非平穩特性，且該模型與規范結合緊密，從而可以方便地用于工程實踐．對范和港跨海大橋的抗震分析表明，豎向地震激勵對墩底軸力的可靠度有較大的影響，因而在進行橋梁設計時需重點考慮豎向地震激勵對主墩墩底軸力的影響．