基于地基載荷板試驗的弦線模量探討

雷勝友 惠會清

(1.長安大學 公路學院， 西安 710064；2.長安大學 理學學院， 西安 710064)

1 弦線模量提出的學術背景

20世紀的五六十年代，中華人民共和國剛剛成立，百廢待興，全國出現了大規模的基本建設．為此，科研設計單位進行了大量的地基承載力試驗，其中在西北地區進行了大量的黃土以及濕陷性黃土浸水濕陷后的承載力試驗，主要集中在陜西、甘肅、寧夏等省份．在這樣的大環境下，出現了這樣的一件事，西安機瓦廠供輪窯使用的煙囪1965年9月底開始施工，年底基本建成，煙囪總高度57.57米，1967年10月發現向西南傾斜84 cm，1969年4月達到93.4 cm，當時各級部門對這件事都十分重視，希望在不破壞煙囪的情況下將已經傾斜的煙囪扶正，以當時的技術和條件，這是件十分棘手的事情，當時有人提出將煙囪拆一半，上面改用鐵皮煙囪，地基浸水加壓校正，也有人主張地基硅化，拆除重建，當時年輕的技術員焦五一先生經過深入思考，提出在煙囪所在地就近進行了地基載荷板試驗，根據載荷板試驗所得P-S曲線，計算得到不同荷載下的地基模量，又大膽地思索，獨辟蹊徑，將該模量和地基附加應力有機地聯系在一起，得到了地基不同深度處的弦線模量，然后采用分層總和法計算煙囪地基的總沉降量，進而制定出實施反壓糾偏方案，成功地將傾斜煙囪扶正[1]．焦五一先生參加完成了大量的黃土地基載荷板試驗及其浸水濕陷后的載荷板試驗，隨后順著前述思路，對大量的試驗資料進行綜合分析和合理取舍，形成了黃土弦線模量與土性和地基附加應力的關系，進而系統地分析了全國地基載荷板試驗資料，形成了中國地基土弦線模量數據庫和計算方法，并編寫了計算軟件[2]，成功解決了200余項工業與民用建筑的地基處理和糾偏問題，提出了世界上著名的意大利比薩斜塔的糾偏方案，該方案被采納實施后，當反壓加到600 t時，斜塔出現了晃動，當反壓加到900 t時，比薩斜塔傾斜停止了，目前已向游客重新開放[3]．由此可見弦線模量法在民用建筑的地基沉降的精確計算以及建筑物糾偏方面顯示出強大的優勢，為工程界所稱道，豐富了土力學寶庫．然而與土力學發展歷史相比，弦線模量誕生的歷史還是比較短，不為人們所熟悉，筆者經過學習研究[4-7]，談一談弦線模量的合理性、所蘊藏的學術意義，以及在高速鐵路地基沉降計算上的應用，希望進一步挖掘弦線模量的學術價值．

2 地基弦線模量的定義以及在地基沉降計算應用概述

在材料力學上，通常定義有材料的彈性模量，一般由材料的單軸拉、壓試驗所得，其拉伸曲線直線段的斜率即為材料的彈性模量．此外為了研究和應用的方便，還定義了材料的初始切線模量、切線模量、割線模量，另外還有弦線模量．各模量示意圖如圖1所示．

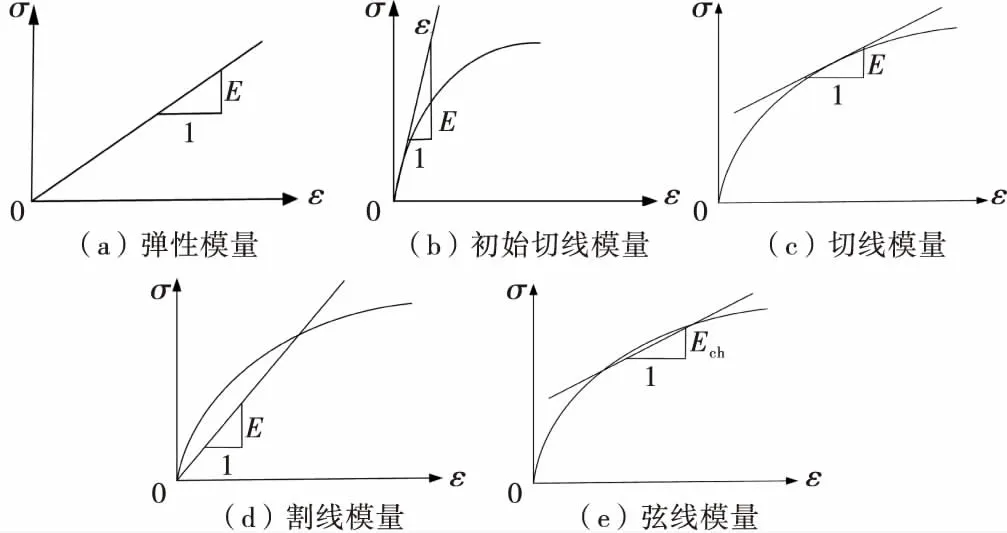
圖1 有關材料的模量示意圖

初始切線模量、切線模量、割線模量、弦線模量都是針對材料的非線性應力應變關系而言．對于巖土類材料，用得最多的是初始切線模量、切線模量、割線模量，而在地基的沉降計算中，常常用到土的壓縮模量，它是由土的室內壓縮試驗所得到．

3 地基土弦線模量的定義、獲取方法及在沉降計算中的應用

3.1 地基土弦線模量的定義、獲取方法

一般由地基載荷板試驗可以得到荷載與載荷板下沉量的關系曲線，即P-S曲線(如圖2所示)，從曲線可以看到，在剛開始加荷階段，荷載和載荷板沉降量近似呈線性關系，當越過比例極限后，隨著荷載的繼續增加，二者之間呈非線性關系．對于P-S曲線的線性段，其直線的斜率就是該荷載范圍內地基的變形模量，對于曲線段，通過分段線性化求得不同荷載下地基的變形模量，通常以差分代替微分的形式來處理，這樣可得到變形模量隨荷載的變化曲線，即變形模量-荷載曲線．

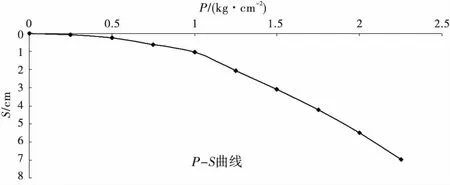
圖2 地基載荷板試驗曲線

3.2 弦線模量法計算地基沉降的基本原理

焦五一先生認為地基的附加應力符合布辛尼斯克法分布，假定在某一深度處地基的附加應力為pi，在變形模量-荷載曲線上內插即可求得不同附加應力pi所對應的地基變形模量，這樣就得到了外荷載下地基變形模量隨深度的分布曲線，然后用分層總和法求得地基的總沉降量(如圖3所示)．在以上計算過程中，將地基土作了均勻化處理．焦五一先生將以上計算所用的地基模量先后稱為變形模量、切線模量、弦線模量，最終定為弦線模量，并一直沿用至今．

從有關資料[1]可知，地基土的變形模量隨深度增加而增大，因此用地基附加應力在載荷板試驗曲線上進行內插而得到地基變形模量，也符合以上變化規律，因此地基模量采取這樣的方法獲取是可行的．以下為弦線模量的計算公式[1]，

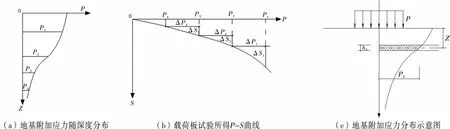
圖3 弦線模量的基本原理

其中，ΔPi為P-S曲線上Pi點前一段的增量，可取載荷板實驗的每級加荷量，即0.25 kg/cm2，ΔS為對應于ΔPi的沉降增量，F為荷載板的面積，d為載荷板底換算直徑，μ為直線變形階段的泊松比．

用弦線模量計算地基總沉降量下式

其中hi為地基分層厚度，βi為修正系數，通常取1．

3.3 弦線模量法在地基沉降計算上的應用

焦五一致力于弦線模量的研究，先后用弦線模量計算了大量的建筑物(包括煙囪、電視塔、比薩斜塔、工業廠房、民用建筑、油罐)地基沉降量和黃土地基的濕陷變形量，其計算的地基沉降量、黃土濕陷變形量與實測值很接近[8-20]，現列出代表性結果如圖4所示．

圖4 弦線模量計算結果比較

為了驗證弦線模量在地基沉降計算上的合理性，筆者也嘗試著用弦線模量法計算高速鐵路路基下地基土的總沉降量[21]，其中地基附加應力分別按布辛尼斯克組合合法、布辛尼斯克直接法、布辛尼斯克三角形法、德國DB836法計算，路基下的地基為經CFG樁+短樁處理過后的復合地基，計算所用的弦線模量是由以上4種方法計算的附加應力，并根據現場載荷板試驗資料內插而得，各處的沉降計算結果如圖5所示．可以看出用弦線模量計算所得的沉降量與實測值比較接近，且精度非常的高，完全滿足高速鐵路工后沉降不大于15 mm的要求．從以上可以看出弦線模量用于地基沉降變形和濕陷變形的計算都是可行的，其準確程度很高．

圖5 西寶高速鐵路客運專線岐山段中心線處地基總沉降量比較

4 由弦線模量引發的思考

4.1 載荷板所得P-S曲線可視為一種本構關系

將載荷板試驗中的荷載P除以載荷板的面積，就得到應力p，同樣以載荷板的半徑或邊長去除S，得到視應變，這樣就得到P-S/B曲線，這樣的曲線實質上就是應力應變曲線，即一種本構關系，所以P-S曲線是一種廣義的本構關系，這時的受荷材料是載荷板下的土體．既然是土體的本構關系，就可用于地基的沉降計算，因此，用布辛尼斯克法所得地基附加應力內插求得弦線模量，然后計算地基沉降變形，就是合理的．如果將地基土均化對待，那么地基土可視為一種理想的均勻材料，每一個荷載就對應一個弦線模量，這樣就可以建立荷載和弦線模量的對應關系，進行地基的變形計算，所以說弦線模量為地基的變形計算提供了一個新思路．

通常進行載荷板試驗時，總是分級加壓，每一級荷載就要在地基中產生附加應力，由附加應力引起地基附加沉降，前后兩級荷載所引起的總沉降量之差，就是后一級荷載引起的沉降量增量．所以說每一級荷載下的地基總沉降量的計算，總是先求得地基附加應力分布，然后內插，得到不同深度處的地基弦線模量，進而得到各層的壓縮量，求和得總沉降量．所以P-S曲線就是累加荷載與總成沉降量(累加沉降量)的關系曲線．

弦線模量與材料性質、應力水平有關，對于土而言，材料性質包括了液限、空隙比、含水量、密度，應力水平則為附加應力的大小．建立起弦線模量與土性和附加應力的關系，或形成數據庫，可用于各種地基沉降計算．如果載荷板下的土體是均質的，就得到均質土對應不同荷載下的弦線模量，即弦線模量是土的一種力學參數，跟土性、應力水平密切相關．用弦線模量法計算地基沉降，只認為地基是某種工程材料而已，僅考慮附加荷載產生的變形，不計及其自重，因為多數情況下，自重作用引起的變形已經發生了，這是與傳統地基沉降計算的不同之處．

4.2 弦線模量方法與傳統土力學方法的比較

一般教科書上的e-p曲線是由室內壓縮實驗得到，由于e值的變化反映了土樣的豎向變形，所以說e-p曲線也是一種變形荷載曲線．從曲線的特點可以看出(如圖6(a))，隨著荷載p的增加，e值越來越小，曲線的斜率是越來越大，表現為土體的壓縮模量是隨荷載的增加而增加．而載荷板試驗所得P-S曲線則是斜率越來越小(如圖6(b))，即土體的弦線模量是隨荷載的增加而變小，所以從曲線的變化特點看，e-p曲線和P-S曲線反映的規律不同．究其原因，是試驗方法的不同所致．也說明載荷板試驗反映了地基土體在荷載下的變形特點，而土的室內壓縮反映了小土試件在側限壓縮條件下的變形特點，兩種試驗的變形特點不同，因此將室內土的壓縮試驗成果用于地基土的沉降計算，在方法上是不妥的．

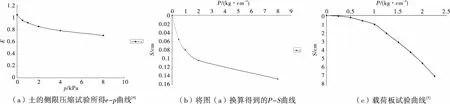
圖6 室內壓縮試驗曲線與載荷板試驗曲線比較

載荷板試驗反映了地基的實際變形，即地基土既有豎向變形，也有側向變形；而室內壓縮試驗反映的則是地基土只有豎向變形，而無側向變形，顯然它不能反映地基真實變形情況．由此可見弦線模量在反映地基的變形特點上比壓縮模量更符合實際情況．這也是兩種方法計算地基沉降的差異所在．

從e-p曲線的使用情況可知，隨著深度的增加，自重應力越來越大，附加應力越來越小，壓縮模量越來越大，每層的壓縮變形越來越小，變形最終趨于收斂．從壓縮量隨深度的變化規律看，兩種方法計算出的總壓縮量隨深度的變化規律是相同的．但是計算所得的沉降量不同，唯一原因就是所采用的地基模量的差異所致．從地基附加應力的分布特點可知，附加應力隨深度的增加表現為“上大下小型”，即沿深度呈“大肚子形”，從載荷板試驗曲線可知，弦線模量隨荷載的增大而變小，即荷載越大，模量越小，反之亦然．所以可想而知弦線模量隨地基深度的增加越來越大，表現為“上小下大型”，壓縮模量則表現為“上大下小型”．而地基的沉降變形量主要來自于附加應力比較大的那部分地基土的變形，因此，附加應力影響范圍內地基土模量的合理選擇是至關重要的，將關乎沉降計算的準確程度．

由于載荷板試驗屬現場原位試驗，所得的弦線模量反映了外荷載下的地基總變形隨地基總附加應力的變化情況，因而用弦線模量計算地基沉降，其精確度較高，而壓縮模量則要差些，其計算結果總是要做修正．從實際計算結果可知，用壓縮模量計算出的沉降值很大，究其原因，主要是由于自重應力隨深度的增加越來越大，而附加應力隨深度的增加越來越小，尤其在外荷載的影響范圍內，自重應力還是很小，而附加應力值卻很大，計算出的地基壓縮量很大，說明計算所用的壓縮模量小．

從e-p曲線的特點看，自重應力很小時，曲線很陡，當有一個很大的附加應力增量時，曲線又變得很緩，綜合而言，用于沉降計算的附加應力增量范圍內的壓縮模量值還是很小，故計算出的沉降量大，這正是由e-p曲線特點所決定．所以說由附加應力“大肚子部分”計算所得的沉降量，在總沉降量中所占比例很大，所以說在沉降計算中，該范圍內地基土的模量是選用弦線模量還是壓縮模量，其計算結果大不一樣．在這一影響范圍內壓縮模量小的原因主要是取樣擾動、土樣的運輸和制備等造成了土樣的初始孔隙比變大，導致計算的沉降量大很多．

4.3 切線模量、變形模量和弦線模量的關系

從數學角度講，如果載荷板試驗所得P-S曲線可以寫成某個函數，通過求導，可以求得曲線在各個點上的導數，而各個點導數值就是曲線在各點上的切線模量，實質上這時的切線模量也是變形模量，而不是彈性模量，因為土體的變形包含了彈性變形和不可恢復的塑性變形．如果載荷板試驗所得P-S曲線不能寫成某個函數表達式，這時要求某一點的斜率就十分的困難，但是可以求得某荷載點鄰域內隨變形的平均變化率，即弦線模量，可用差分代替微分的方式求得，所以從這點上講，弦線模量就是切線模量，都屬變形模量．所以之前文獻稱弦線模量為切線模量也是對的[1]．

對于載荷試驗所得P-S曲線，還可以通過非線性插值的方法，得到插值函數，這樣既確保每級荷載下的弦線模量是準確得，又可通過求導得到其他點荷載下的弦線模量，更為可貴的是可以通過這樣的方法，可以求得第一級荷載以前的弦線模量，使得用這種方法計算更深處地基的沉降成為可能，進一步提高用弦線模量計算地基沉降的精度．在這里筆者一直認為，內插是可靠的，外推是不可靠的，基于這一點，載荷板試驗P-S曲線范圍以外的弦線模量是不可靠的．也有文獻假[7]設P-S曲線是雙曲線，則可以用求導的方法得到所謂的切線模量和割線模量，然后用于分層總和沉降計算，對于用任意曲線的切線模量可用于沉降計算，總的來說在實質和弦線模量是一樣的．

4.4 弦線模量法體現了土力學“有效”的含義

在載荷板試驗中，p屬重力以外的荷載，所以s為荷載p作用下，載荷板下土體豎向變形總和，P-S曲線實質上還可寫為P-∑Si關系曲線，Si為地基不同深度處的豎向變形量，隨著外荷載的增加，而其中的p也是累積的結果，又可理解為∑Pi-∑Si關系曲線，也就是由于P的作用，而產生了地基附加應力，由于附加應力的作用而產生了地基附加變形，從而體現有效的含義．荷載板下地基某一深度處的應力之和，就是累加荷載∑Pi，或者p，如果將地基視作一個大的“試件”話，試件橫截面上處處所受的荷載都為p，自然試件總的變形量應為各段變形量之和．因此P-S曲線實質上就是這個“大試件”的應力變形曲線，當然可以用于試件各分段的變形計算．

由于載荷板試驗是先施加荷載，然后地基產生變形，就相當于應力控制式加載過程中，即變形是隨著荷載的發展而發展，按照函數關系，自變量為荷載，因變量為變形量．在載荷板實驗的加載過程中，對于每一級荷載Pi，都會在地基中產生不同的附加應力，都會產生不同深度處的變形，進而產生不同的累加變形，在彈性范圍內，附加應力隨深度的分布曲線形式是不變的，即荷載大小的變化只改變曲線的數值，而不改變其形狀．在彈性范圍內，即所有土層的變形增量，與荷載的增量成正比，進而可知，累加變形量與累加荷載成正比，因而載荷板P-S曲線就反映了地基中的附加應力和變形的關系，因而P-S曲線可以用于附加應力下地基的變形計算．

4.5 在處理沉降計算時所用方法的不同

用弦線模量方法計算地基沉降可以說是直奔主題，直接對準目標，計算出的沉降量不需要修正，所用的應力為外荷載產生的地基附加應力，由附加應力引起的變形即為地基沉降變形，這樣理解起來，概念清晰，體現了土力學中“有效”應力的意義．這同傳統沉降計算在戰略思想上是不同．

4.6 弦線模量的發展歷史考證

大量的國內外資料表明，弦線模量提出最早可以追溯到1967年[2]，當時西安石油儀表廠房屋地基出現了浸水后的大的濕陷變形，焦五一用弦線模量的方法成功地解決了地基處理問題，并先后解決了大量的地基處理難題，而美國才在1982年金屬規范里出現了初始切線模量、割線模量、切線模量、楊氏模量，隨后經過一次次的規范修訂，在最新的規范里，只保留了楊氏模量和弦線模量，由此可見，隨著荷載的增加，材料會出現大的非線性變形，用弦線模量可以很好地描述材料這一特性，并且在定量分析上具有可操作性，而通常意義上的切線模量則很難做到這點．可以斷言，弦線模量可用于一切材料的非線性變形計算，如金屬、巖石、水泥等，為所有材料的應力-應變非線性變形計算分析提供了一條新途徑．

對于線彈性材料而言，楊氏彈性模量、切線模量、弦線模量是同一個量，對于非線性彈性材料，弦線模量又顯示出它的不同意義．由此可見，我國學者焦五一提出的弦線模量要比國外早15年，在使用方面也比國外好．

4.7 弦線模量其他應用及最新進展

如果載荷板試驗的最后一級荷載加完后又是分級卸載，所以還可以得到其卸載曲線或者回彈曲線，通過回彈曲線可以得到每一級荷載下的彈性變形增量和彈性模量，如果每級荷載下的彈性模量值不同，這正體現了土體的特性，這時又根據弦線模量的思路計算每一級荷載下的彈性模量．

黃土浸水濕陷變形也最終歸結為土的弦線模量的降低，這樣計算可以不必過分地強調濕陷變形，就按弦線模量計算而已．用弦線模量計算地基沉降不涉及地基土超固結性的判斷，不需要進行室內壓縮試驗，其計算的思路可用于任何土．由于土的復雜性和實驗的可操作性，以及研究經費等，研究者通常大多采用室內試驗方法來研究土，其實驗所用的土大多為經過擾動的原狀土或重塑土，這樣得到的實驗結果很難描述實際中的土，尤其在力學特性方面，其差異就更明顯，例如由室內實驗研究所得土的本構關系很難用于實際工程中土的應力變形計算，這樣使得人們不得不尋求一種現場土力學的方法，以獲取土的相關參數，無論是為工程應用服務還是為土力學研究，都顯得十分必要，而弦線模量則體現了這點．

通過載荷板試驗，獲取土的弦線模量，通過地勘資料，使其與土性發生聯系，可用于全國范圍的地基沉降計算，勢必是一個新的途徑，因此開展土的原位試驗技術，并用于工程實踐，這將是未來土力學的一個發展方向．

5 結 語

本文研究表明，地基載荷板試驗曲線實質上為一種原位本構關系，可用于地基沉降計算．大量工程證明，用弦線模量法計算出的沉降值同實測結果比較接近，這種地基沉降計算方法完全不同于傳統土力學的地基沉降計算方法，同時也說明，當材料進入非線性階段，其模量不僅與材料的性質有關，還與應力水平有關．弦線模量法的研究思路還可用于其他材料的非線性變形計算，還需進一步挖掘弦線模量的學術意義．載荷板試驗所蘊含的內容相當豐富，涉及到地基承載力、地基附加應力分布、沉降計算、地基模量的選擇、地基破壞形式，以及土性等，還需進一步挖掘分析載荷板試驗資料所蘊含的更多信息．