基于反演法的嚴格反饋非線性系統模糊自適應約束控制
宗學軍, 吳振強
(沈陽化工大學 信息工程學院, 遼寧 沈陽 110142)
嚴格反饋形式的非線性系統控制研究吸引了越來越多研究者的關注,系統輸出的跟蹤控制問題是工業領域中一個重要又實際的研究課題[1].然而實際系統的非線性特性以及不可避免的不確定性因素的存在對系統的輸出跟蹤都能造成巨大影響,因此對于這類不確定非線性系統的跟蹤控制問題研究具有非常重要的現實意義.基于反演(backstepping)法的自適應控制已研究多年,其有效解決了一類不確定非線性系統的自適應控制問題.它從系統最低階微分方程開始,在每一步的設計過程中引入虛擬狀態和虛擬控制,并在最后一步設計出實際控制律[2-3].另一方面,傳統的自適應控制技術還不能完全解決非線性系統中出現的能夠影響控制系統性能的極為復雜的不確定性.因此,利用模糊邏輯系統的萬能逼近性能去辨識系統中的不確定項是一種新的方法[4-7].
性能約束問題一直是許多工業控制系統中最重要的研究課題之一,它可以防止系統遭受損壞.其主要思想是在保證系統穩定的前提下還可以滿足系統的暫態和穩態性能.近年來,約束控制方法的研究已經取得了一些進展[8-11].其中預設性能控制(prescribed performance control,PPC)方法的關鍵就是采用一個轉換函數把原始系統的誤差轉換成一個新系統的新誤差.而這個轉換函數的逆變換則被作為設計自適應控制器的一個變量.只要轉換后的誤差系統穩定,系統的跟蹤誤差就會保持在預設的誤差邊界之內[7].
基于以上分析,本文考慮一類嚴格反饋非線性系統的自適應跟蹤約束控制問題.結合模糊邏輯系統解決了系統中的不確定項.設計了一個新的約束變量來保證非線性系統的暫態和穩態性能.利用Lyapunov方法,證明閉環系統中的所有信號都是半全局一致最終有界的,且跟蹤誤差可以收斂到原點附近的一個較小鄰域內.
1 問題的描述
1.1 系統描述
考慮如下的不確定嚴格反饋非線性系統:
(1)
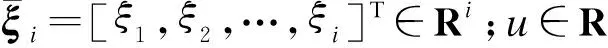
引理1[12]如果F(Z)被定義為密集ΩZ上的連續函數,則存在模糊邏輯系統WTQ(Z),其能夠以一個理想的精度ε>0去逼近任何連續非線性函數,使得
(2)
其中:W=[w1,w2,…,wn]T是理想的權值向量;Q(Z)是基函數向量.
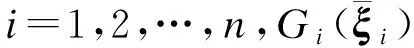
1.2 約束變量
預設性能邊界函數Bψ(t)的定義如下:
Bψ(t)=(ρ0-ρ∞)e-βt+ρ∞,
(3)
其中:ρ0是邊界函數Bψ(t)的初始值;β是指數函數的收斂度;limt→∞Bψ(t)=ρ∞.ρ0,ρ∞和β是預設定常數.
定義跟蹤誤差e1=ξ1-yr,其中yr為已知的有界的跟蹤信號,且它的導數也是已知有界的.在自適應模糊控制器的反演設計過程中,提出一種新的約束變量,其定義如下:
(4)
對ι1求導可以得到:
(5)
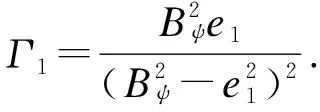
2 自適應模糊控制器設計
采用反演技術設計自適應控制器,首先設計虛擬控制信號αi和實際控制輸入u:
i=2,3,…,n
(6)

(7)
ci為未知常數,后面將給出Wi.在該控制器設計中采用了反演方法,虛擬狀態變量定義為:
zi=ξi-αi-1,i=1,2,…,n,z1=e1,α0=yr.
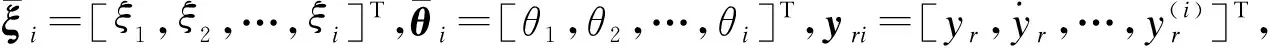
i=2,3,…,n-1
(8)
自適應律的定義如下:
(9)
其中:i=2,3,…,n;ri和σi為設計的正參數.
控制器的設計過程共分為n步.
第1步 考慮系統(8)中的第一個子系統,選擇以下Lyapunov函數:
(10)
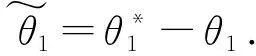
由z2=ξ2-α1,推導出V1導數:
(11)
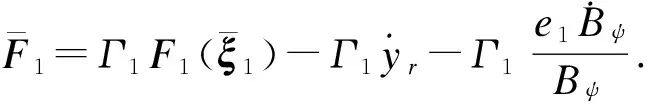

|δ1(Z1)|≤λ1.
(12)
其中δ1(Z1)是逼近誤差.
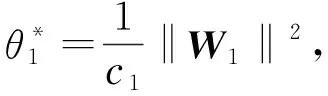
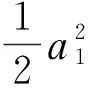
(13)


(14)
(15)
將式(13)和(15)代入式(11)中,得到:
(16)
(17)
第j步j=2,3,…,n-1,考慮下面的Lyapunov函數:
(18)
Vj導數為:
(19)
則有:
(20)
(21)
由于ξj+1=zj+1+αj,式(21)可以得出如下形式:
(22)
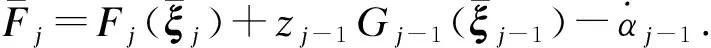
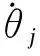
(23)
第n步 考慮以下Lyapunov函數:
(24)
Vn導數為:
(25)
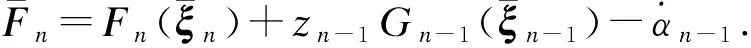
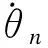
(26)
3 穩定性分析
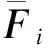
(1) 閉環系統中的所有信號均為半全局一致最終有界.
(2) 輸出跟蹤誤差e(t)=y(t)-yr(t)小于預設的界限,并且滿足暫態過程和穩態的預設性能.
證明:(1)由于
(27)
將式(27)帶入式(26)中,得到:
(28)
設置控制參數如下:
(29)

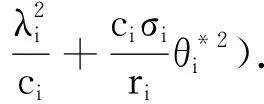
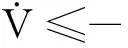
(30)
由不等式得到:
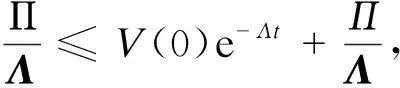
(31)
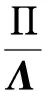
(2) 由V1和式(31)可知:
(32)
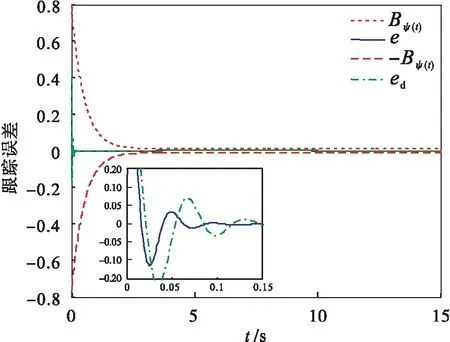
從Π>0,Λ>0,0 V(0)e-Λt≤V(0). (33) 式(33)代入式(32)可得: (34) (35) 即: (36) 因此可得: (37) 即: (38) 因此可以看出,輸出跟蹤誤差小于預設的界限,通過選擇合適的設計參數,誤差可以任意小. 考慮單連桿機械手臂動力學系統的數學描述如下[14]: (39) 其中:M為負載端慣量;m為負載質量;L為連桿長度;u表示電機的輸入電壓. 機械手臂的參數設置:m=1 kg,M=0.5 kg·m2,L=1 m,g=9 m/s2.跟蹤誤差的預設性能參數設置:邊界函數的初始值ρ0=0.8,穩態誤差ρ∞=0.01,最小收斂速度β=2.選取控制參數值為:k1=150,k2=30,a1=5,a2=2,r1=r2=0.25,σ1=5.25和σ2=0.25.初始條件設為[ξ1(0),ξ2(0)]T=[0.4,2.5]T,[θ1(0),θ2(0)]T=[0,0]T.理想輸出軌跡為yr(t)=sin(0.5t).仿真結果如圖1~圖4所示. 由圖1和圖2可以看出,與參考文獻[2]的一般動態面控制(DSC)方法相比較,采取相同的參數設置,本文所提方法下系統的超調量更小.自適應參數變化曲線和控制量輸入u分別如圖3和圖4所示.仿真結果表明,本文所提出的控制方法具有較好的跟蹤性能,且跟蹤誤差被限定在預設的約束范圍之內. 圖1 系統的實際輸出y,一般動態面方法的yd,理想輸出yr 圖2 系統的跟蹤誤差e,一般動態面方法的ed 圖3 自適應參數曲線 圖4 控制量輸入u 建立了一種用于不確定嚴格反饋非線性系統的軌跡跟蹤反演控制方法.通過設計約束函數以實現跟蹤誤差的預設性能控制.仿真結果的實際輸出與一般動態面方法的輸出相比較,可以得到機械手臂動力學系統的跟蹤性能較好,調節速度較快.仿真結果的跟蹤誤差與一般動態面方法的跟蹤誤差相比較,可以得到機械手臂動力學系統的超調量更小,振蕩較少,且跟蹤誤差被限定在約束范圍之內.所以仿真結果表明了性能約束的自適應反演控制方法的有效性和可行性.
4 仿真結果與分析



5 結 論

