關于零模正則化邏輯回歸問題的研究
呂佩雯
(華南理工大學,廣東 廣州 510640)
一、引言
設Rn是賦予了內積及誘導范數的有限維向量空間,考慮稀疏邏輯回歸問題:令為樣本,為類別標簽,則邏輯回歸模型為:
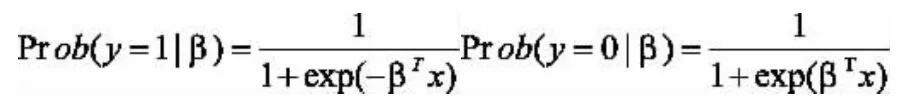
其中Prob(y=1/β)是在給定樣本觀測值β后,類別標簽為l的條件概率,x為特征向量。
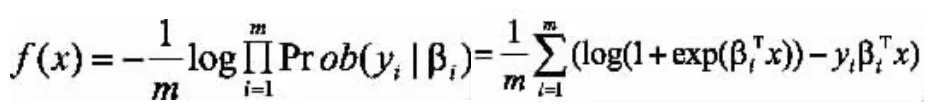
這是一個光滑的凸函數[1,3],可以通過最小化邏輯損失的均值來求解特征向量x。
二、零模正則化
當訓練集里的樣本數m小于維數n時,直接求解容易出現過擬合,一般使用正則化來避免過擬合問題的出現。本文將使用零模正則,即求解零模正則極小化問題:
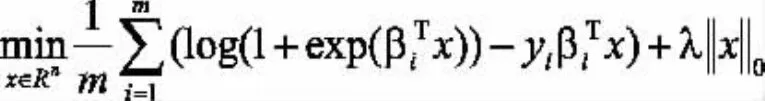
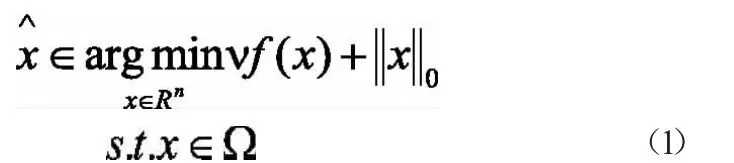
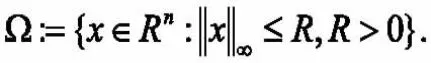
零模優化問題是一類帶有組合性質的向量優化問題,(1)這種問題在計算上通常是NP難的,難以求得其全局最優解。而且,源于實際應用的零模優化問題通常具有較高的維數,根本不適合采用全局優化方法去尋求全局最優解。一個常用的處理方法是使用凸松弛技術,這種方法通過解一個或一系列易于處理的凸優化問題來產生一個理想的可行解或局部最優解。
三、零模正則化問題的等價模型
首先,從零模函數的變分刻畫入手,可以得到零模正則問題的等價全局Lipschitz連續優化模型。對任意的,容易得到:
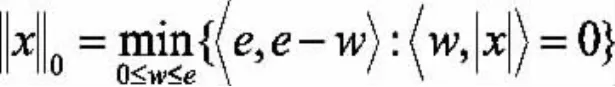
因此,問題的等價問題為:
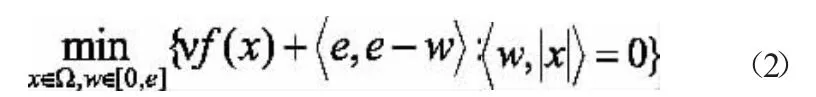
問題的可行集中包含著如下互補約束條件:
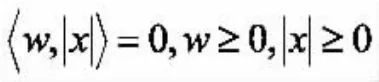
這說明零模正則化問題也是一個帶有互補約束的數學規劃問題(MPEC)。需要注意的是,MPEC在優化中也是一類很難的問題。雖然問題(2)的目標函數比原問題(1)簡單,但卻含有非凸互補約束,這比非凸目標函數更難處理。為解決這個非凸約束,考慮問題(2)的罰問題:
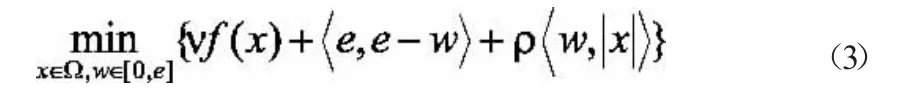
其中ρ>0是罰參數。下面的定理1將說明問題(3)是問題(2)的全局精確罰,即他們有相同的全局最優解集[5]。在此之前,先建立定理證明需要用到的引理。
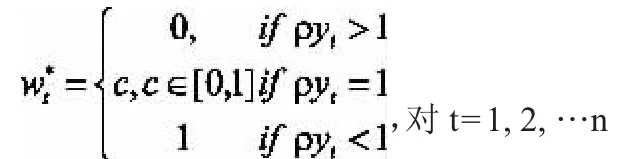
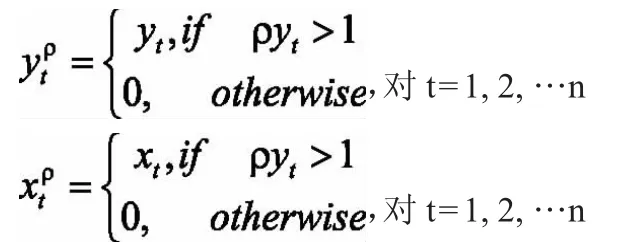
引理2.設函數f在集合上全局Lipschitz連續,若ρ>VLf,則對任意的和,有:
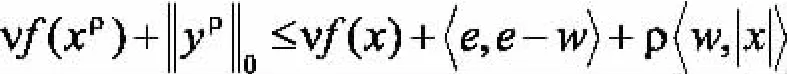

所以,只需證明:
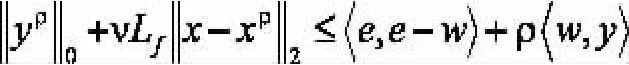
由引理1,若wρ是下面問題的最優解則wρ的形式可以為對t=1,2,...n.所以,
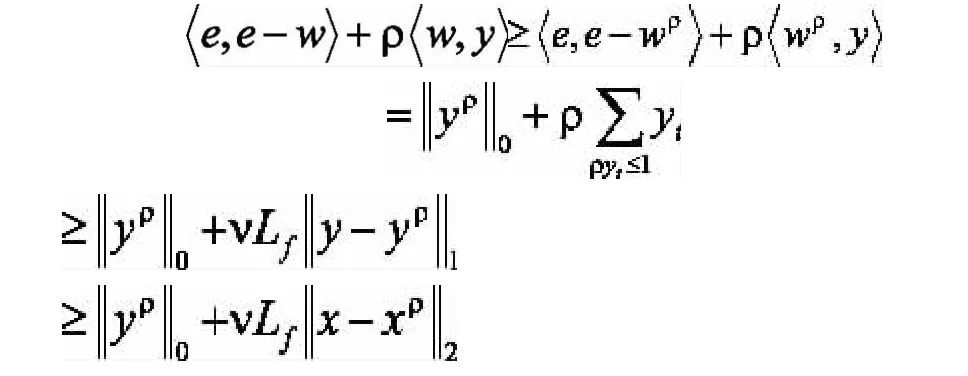
第一部分得證。下面證明第二部分:當等式成立時,
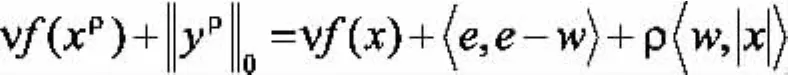
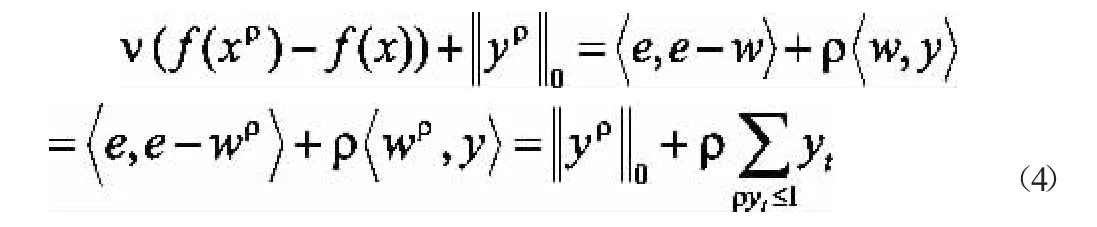
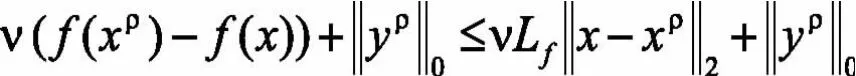
所以,
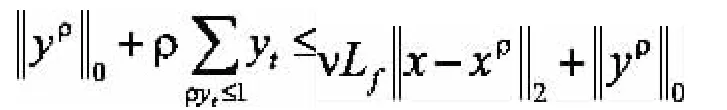
再加上ρ>VLf,可得:
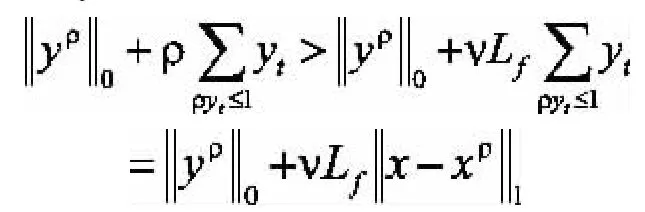
下面給出問題(3)是問題(2)的全局精確罰的理論保證:
證明.設問題(2)和問題(3)的可行集分別為 S 和 Sρ,問題(2)和問題(3)的全局最優解集分別為S*和S*ρ。令ρ>vLf,首先證明:對任意的,有,且由引理2,
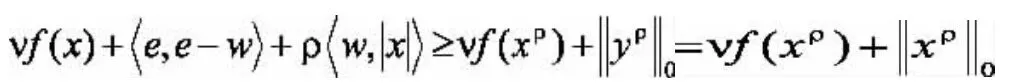
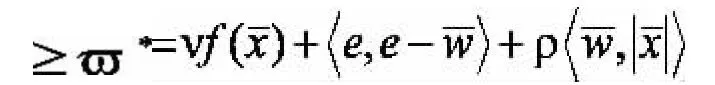
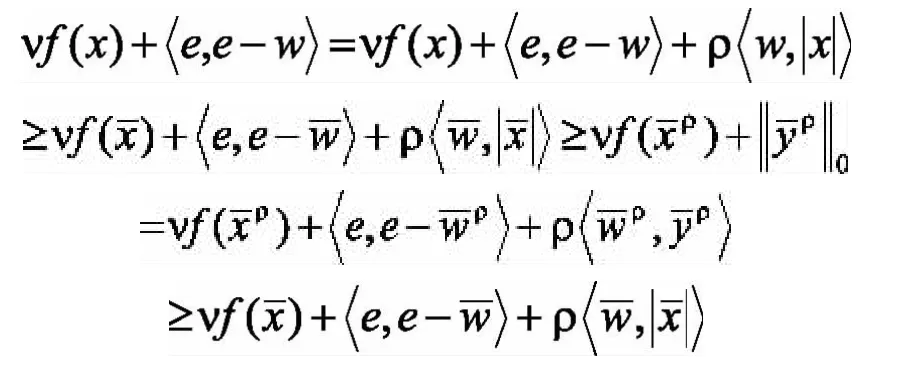
所以,
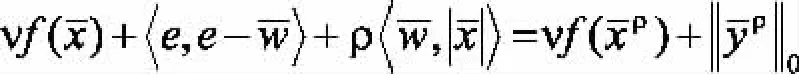
這樣,求解問題(1)轉化為求解罰問題(3)。雖然罰問題(3)非凸,但是這種結構使得它比零模正則化問題更好解決。當變量w選定時,f(x)為邏輯損失函數,罰問題(3)退化為關于x的凸的極小化問題;當變量x選定時,罰問題(3)退化為關于w的凸的極小化問題,這樣的問題是有閉式解的。為此,針對f(x)為邏輯損失函數,將選用多階段凸松弛法[4]來求解問題(3)。多階段凸松弛法的主要步驟為:
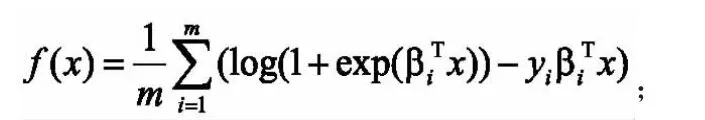
(S2)求解極小化問題:
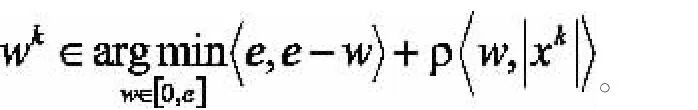
由引理1可知Wk是容易求得的,該方法的主要工作都在于解決一個加權的L1-正則化邏輯回歸問題[6,9,10]。這是一類凸優化問題,所以它可以通過標準的凸優化方法求解,比如:增廣拉格朗日法,內點法[7],IRLS-LARS[8],路徑跟蹤法,迭代加權最小二乘法等。
四、結束語
本文借助零模函數的變分刻畫,將零模正則化邏輯回歸問題等價的寫為帶有互補約束的數學規劃問題(簡稱MPEC問題);然后證明將互補約束直接罰到目標函數上所誘導的罰問題是MPEC問題的全局精確罰(即與MPEC問題有相同的全局最優解集)。正如文中所說,此精確罰問題的目標函數不僅在可行集上全局Lipschitz連續,而且還具有滿意的雙線性結構,為設計零模正則化問題的多階段凸松弛算法提供了滿意的等價Lipschitz優化模型。

