基于改進遺傳算法的動態路徑規劃研

董小帥 ，毛政元

1.福州大學 福建省空間信息工程研究中心，福州 350002

2.福州大學 空間數據挖掘與信息共享教育部重點實驗室，福州 350002

3.福州大學 地理空間信息技術國家地方聯合工程研究中心，福州 350002

1 引言

按照對時變性因素的不同處理，路徑規劃模型分為靜態和動態兩種類型[1]，前者指在靜態路網模型上迭加各路段權重，再采用規劃與優化算法求解最佳路徑，同一問題只需求解一次；后者指綜合考慮路網中各路段的通行能力和路網不斷變化的路況信息采用優化算法求解最優路徑[2-3]。動態路徑規劃相比靜態路徑規劃更具實用價值[4]，同時，由于其采用的動態路網模型加入了實時、復雜、多變的路網信息，經典規劃算法難以高效、魯棒地完成路徑規劃與優化，目前相關研究中一般采用仿生智能算法實現動態路徑規劃[5-9]。

遺傳算法是一種采用種群搜索機制的全局性尋優算法，該搜索策略使求得最優解的可能性和效率大大提高[10]，該算法因此被廣泛應用于包括路徑規劃在內的眾多問題的求解研究。但是傳統的遺傳算法存在“早熟收斂”、種群多樣性逐漸降低和局部搜索能力差等缺陷[11-14]。對此，相關研究文獻中提出了一系列的改進，比如，采用啟發式算法生成初始種群[15-17]，提出以相同節點作為交叉點的交叉策略和變異策略等[18-19]，提高收斂速度，避免“早熟收斂”；采用多種群協同進化策略[20]，優良基因以一定概率在不同種群間橫向傳遞，降低“早熟收斂”的可能性；自適應交叉概率和變異概率的提出，動態調整交叉，變異操作[21]，使得隨著迭代次數增加，種群多樣性不會大幅降低；引入模擬退火思想[22]以一定的概率接受比當前解更差的新解，混合禁忌搜索算法[23]、爬山算法[24]、融入復合型操作[25]等提高局部搜索能力。這些改進能夠在一定程度上克服傳統遺傳算法的缺陷，但在處理大規模實時交通數據時，求解精度與效率仍不能滿足實時路徑規劃的需求。

本文針對傳統遺傳算法應用于動態路徑規劃求解的局限性提出以下三方面的改進：（1）結合隨機選擇和趨于終點方向提出一種控制全局搜索方向的種群初始化策略，在保持初始種群多樣性的同時提高初始種群個體質量，加快收斂。（2）提出一種根據空間距離的鄰近大小選擇交叉位置點的交叉策略，有效保留父代優良基因，同時避免“早熟收斂”。（3）提出一種基于節點適應度的局部搜索策略，通過建立節點選擇概率與節點適應度的正相關關系，有效提高局部搜索能力，加快收斂。設計與實現了改進的遺傳算法，并以福州市部分路網數據為樣本，驗證改進后的遺傳算法在求解精度、效率與穩定性三方面的進步。

2 動態交通網絡規劃模型

2.1 動態路網模型

在城市交通網絡中，同一路段的交通狀況一般會隨時間而改變，動態路網模型不僅是對現實世界中路網的簡單抽象表達，同時還包含路況的實時變化信息[26-28]。比如，某些路段在上下班高峰時段更擁擠，采用傳統的靜態路阻函數進行時間最短的路徑規劃時，不能有效規避擁堵路段，時間成本較高。動態路網模型是靜態路網模型添加各路段時態信息后的擴展，其數學表達式如下：

式中，G表示有向帶權的動態城市交通路網；V表示路網中節點集合，V={vi|i=1,2,…,n}；E表示路網中各個節點連通的有向路段集合，vj∈V}，vi、vj分別是路段e的起點、終點；T表示時間閉區間[t0,tm]，t0是起點時刻，tm是到達終點時刻，在實際交通網絡中，Δt為間隔時長，其值越小越能實時反應路況信息的變化，一般取5 min，并忽略在該間隔時長內的路況變化；表示節點v在時刻t的時延集合；W(e,t)表示路段e在時刻t的路阻系數集合。

圖1為路網示意圖，其中節點包括轉向延誤節點和分流節點兩種類型，后者不產生轉向延誤（如V2）；路段具有方向性，在同一時間間隔內，同一路段可能由于方向不同而具有不同的路阻系數。

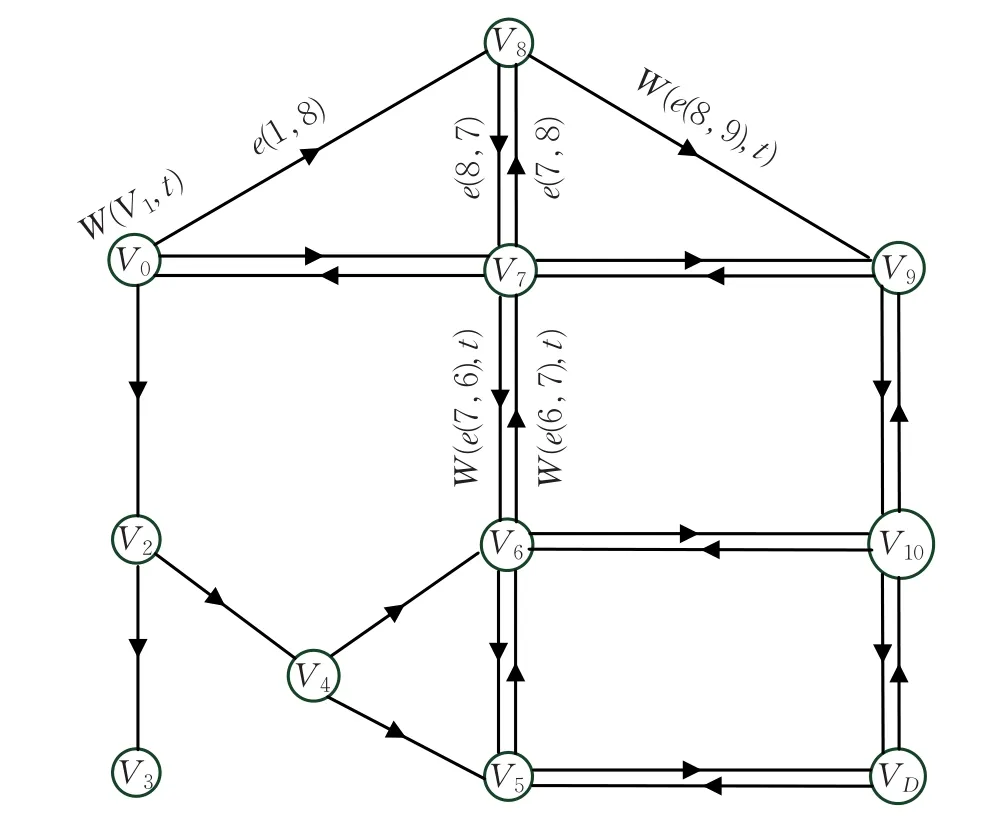
圖1 交通路網示意圖

2.2 路徑規劃模型

如圖1所示，設vO、vD分別是始節點、終節點，ROD是vO到vD所有合格路徑的集合，r=(vO,v2,v4,v5,vD)是其中一條路徑，r∈ROD，時間最優路徑規劃是指根據時刻t所在時間段的路況信息，分別計算ROD中每個路徑的行程時間Z(r)，從中選擇一條時間最短的路徑作為該時間段內的最優路徑，目標函數如下：

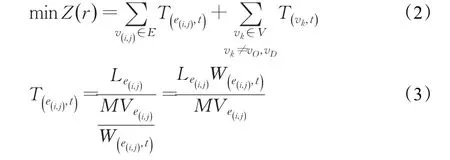
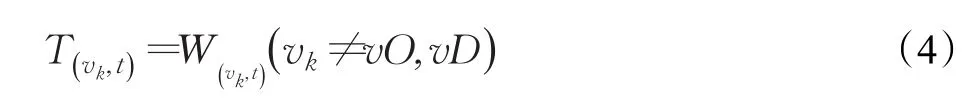
3 改進遺傳算法理論

3.1 編碼和初始化

遺傳算法包括三種常用的編碼實現方式，即二進制編碼、符號編碼與實數編碼。在動態路徑規劃問題中，一條路徑相當于一個染色體，路網節點相當于染色體中的基因，由于這些節點的排列順序正好就是所要求的路徑，所以采用實數編碼方式更能直接表達路徑的實際意義，同時也有利于適應值函數的選取和適應值的計算。由于城市交通路網中的節點數較大，滿足相同起點和終點之間的不同連通路徑一般具有不同的節點數，因此采用變長度染色體編碼策略比定長度策略更適合求解動態路徑規劃這一問題。

遺傳算法與其他搜索算法最大的區別之一就是其面向種群進行搜索的并行性，初始種群的設定對整個遺傳算法的運行性能具有決定作用。傳統的遺傳算法采用隨機的方式生成初始種群，這樣雖能提高種群的多樣性，但整個搜索過程缺乏方向性的引導，同時會出現斷路或環路現象，使得遺傳的進化操作復雜化甚至無意義。為了保證種群的多樣性、避免出現斷路與環路現象，同時又提高初始種群個體的質量，本文采用半隨機方式生成初始種群，即引入控制全局搜索方向的啟發式搜索策略。具體操作步驟如下：（1）以起節點O作為染色體的第一個基因，以終節點D作為染色體的最后一個基因。（2）為了規避斷路或環路現象，當一個節點被選中后，就標記該節點，若當前節點無未標記的鄰接節點可用于選擇時，退回當前節點的上一節點重新進行選擇并標記當前節點禁止下一次被搜索到。（3）以當前節點C的所有未被標記的鄰接節點作為下一個節點N的候選節點，從中按照一定的選擇概率使用隨機方式或最優夾角方式確定下一個節點，若選擇最優夾角方式，計算有向路段的夾角，選擇夾角最小的節點作為下一個節點。（4）重復步驟（2）和（3）直到當前節點C 為終節點D，即為一個初始染色體。（5）按照此方式求解下一個染色體，直至達到初始種群規模的要求。（6）為了進一步提高初始種群個體的平均質量，本文確定初始種群規模為設定種群規模數的1.2倍，最后按表現排名依次舍去最差的多余個體。

3.2 選擇操作

定義適應度函數的值為每個個體所包含路段和中間節點的交通時間阻抗之和，根據第二章得出的動態路網模型和動態最優路徑模型可知，個體適應度函數為：

式中，Z(r)越小，染色體的適應值越小，所對應的路徑所花費的行程時間越少，越接近于路徑最優解。

選擇操作是指從當代種群中選擇優秀個體以生成交配池遺傳給下一代的過程，聯賽選擇、最佳個體保留、適應值比例選擇是目前最常用的三種選擇策略。本文選擇聯賽選擇與最佳個體保留相結合的策略，前者的基本思想為：從當代群體中隨機選擇一定規模的個體，比較后選擇適應值小的個體放入交配池；可通過調整聯賽規模動態控制群體選擇壓力，一般聯賽規模取2。同時采用最佳個體保留策略將當代種群中最優的個體直接復制進入子代，使得子代種群中的最優個體不會出現比父代種群中的最優個體差的可能，從而保證進化方向，加快收斂速度。

3.3 交叉操作

交叉算子是模仿自然界染色體基因交叉重組將父代的優良基因遺傳給下一代個體的操作。采用隨機確定交叉點對或選擇相同節點作為交叉點對的傳統方式進行交叉操作存在明顯的局限性，前者需對子代個體進行連通化處理，從而使父代的優良基因發生劇變；后者會因為兩父代個體在此節點的前后基因片段相同而產生等同于父代的個體，使得交叉操作無效。因此本文采用啟發式鄰近交叉算子操作，主要步驟如下：（1）從其中一個雙親中隨機選擇待交叉點（除去O、D點）。（2）計算另一雙親中的節點與該節點的空間距離，選取距離最小的節點作為交叉點。（3）在交叉點連通生成子代個體，使子代表示的路徑合格化。此策略把需要連通處理的路段降到最小，同時保留了父代雙親的優良基因。

3.4 變異操作

傳統的單點、多點變異等策略在路徑規劃問題中不能有效地維持種群的多樣性，容易導致個體向更壞的方向變異，本文采用多向變異策略，主要步驟如下：（1）按照變異概率選擇變異個體，隨機選擇變異個體的變異點（除去O、D點）。（2）以該點為起點，O點為終點，逆向搜索獲得變異個體。（3）以D節點為起點，該變異點為終點，逆向搜索求得變異個體。（4）對兩個變異個體進行去環路處理。（5）比較兩種方式下變異個體的適應度，選擇適應度大的個體作為子代個體。（6）為保證種群多樣性，每隔五代重新生成一個新的個體取代其中一個待變異個體。

3.5 局部搜索策略

前人引入模擬退火、爬山與禁忌搜索等思想設計的混合遺傳算法雖在一定程度上能提高遺傳算法的局部搜索能力，但由于局部搜索過程中多次隨機生成若干路段，然后比較擇優替代舊局部路段，而沒有考慮或者利用局部路段中鄰接節點的路況、轉向等已知信息的綜合影響，從而導致經過大量時間解算得到的最優路徑中的部分路段為次優而非最優，因此本文引入節點適應度這一新的局部搜索策略對各代種群個體的隨機部分基因片段進行自學習，以替代適應度差的舊基因片段，且每次自學習只需搜索一次。根據路段的實時路況Traffic、路段的道路等級類型Type、轉彎類型Turn，以及與基因片段終點的夾角Angle四個影響因子對當前節點的鄰接節點進行適應度評價，定義為節點適應度，按照適應度所占比例選取下一節點。節點適應度與節點選擇概率定義為：

式中，f(xj)為當前節點的鄰接節點xj的適應度；根據路段的路阻系數，分為通暢、較通暢、擁擠和擁堵四種類型，分別對應的 Traffic值為1、0.75、0.5、0；根據城市交通道路的等級類型，分為主干路和支路兩種類型，分別對應的Type值為1和0.5；通過判斷通往下一節點的行駛轉向，分為直行、右轉、左轉和掉頭四種類型，對應的Turn值分別為1、0.75、0.5和0.25；Angle為有向路段----CN與------

ND的夾角所對應弧度值（C為當前節點，N為待選鄰接節點，D為所選基因片段的終點），由于其與適應度呈為負相關，需要進行倒數處理。P(xj)為鄰接節點xj的選擇概率，節點適應度越大，選擇概率就越大。

3.6 算法步驟

改進的動態路徑規劃算法的主要步驟如下：（1）設定遺傳參數以及動態路阻系數。（2）采用啟發式策略獲得初始種群。（3）計算個體適應度，判斷是否滿足算法終止條件，滿足則算法終止輸出實時路徑轉步驟（6），不滿足轉步驟（4）。（4）進行選擇算子、交叉算子、變異算子操作，對遺傳算子操作生成的子代個體進行局部搜索，并通過篩選生成子代種群。（5）轉步驟（3）。（6）按照最優路徑行駛，每隔5 min更新動態路阻系數，并判斷當前最優行車路線上是否出現某一個或幾個路段發生擁堵等嚴重影響正常通行的現象，若不發生繼續原定路線行駛，若發生轉步驟（7）。（7）定位當前位置的下一節點，若其為終點，結束行程，若不為終點則以該節點為起點重新進行路徑規劃。如圖2為算法流程。

4 實驗與分析

4.1 數據處理

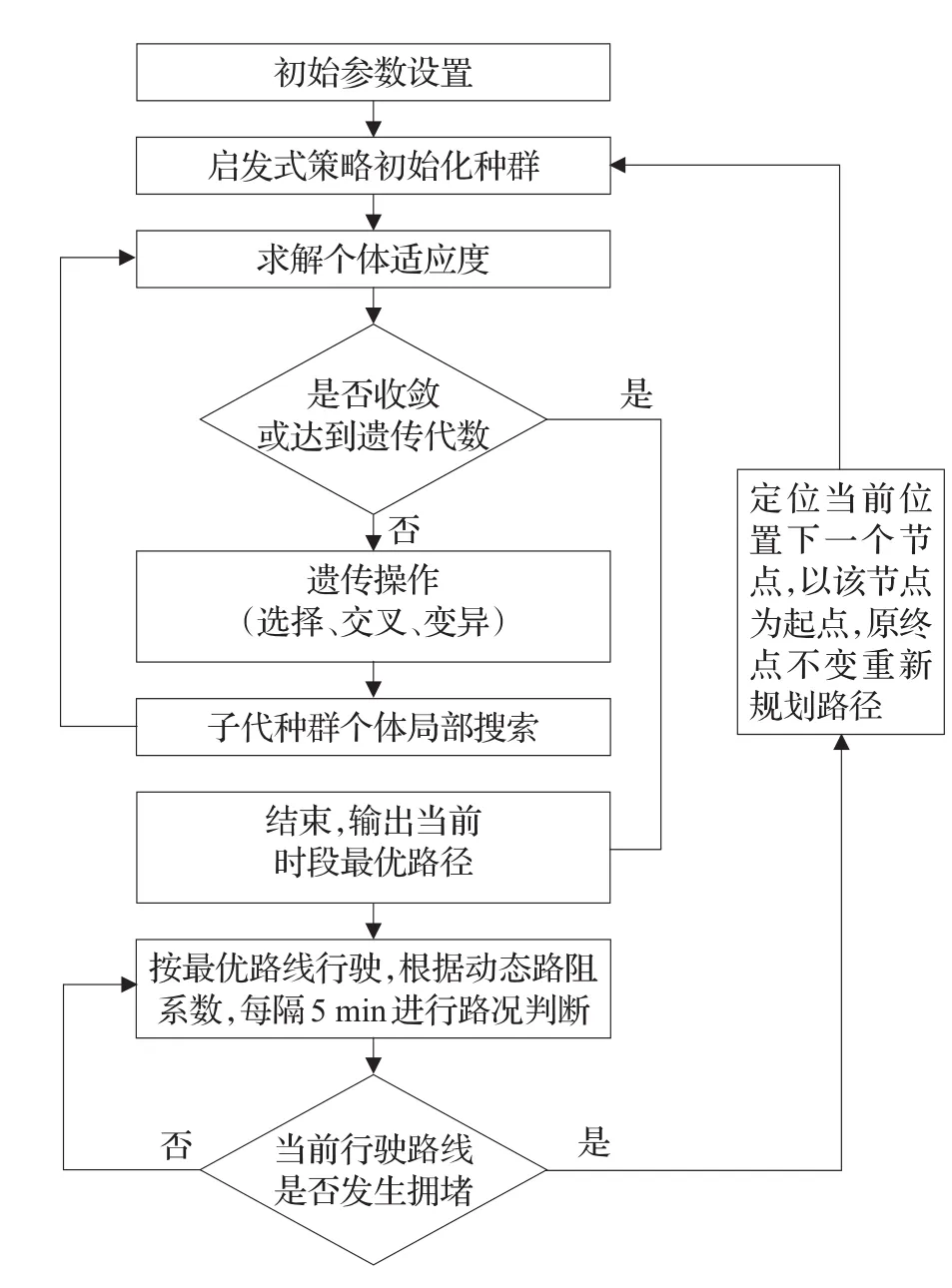
圖2 改進后的算法流程

有向交通路網向量數據主要包括節點圖層和路段圖層，依據時間最短的路徑規劃需求，先設計節點與路段的字段屬性表：前者包括RoadID、FromNodeID、ToNodeID、Road_Type、Speed、Length與Real_Traffic字段，分別表示路段編號、路段起節點編號、路段終節點編號、路段等級、通暢時速度、長度、擁堵系數；后者包括NodeID、X、Y與Node_Type字段，分別表示節點編號、X坐標值、Y坐標值、節點是否為轉向節點；二者通過路段屬性表中的FromNodeID、ToNodeID字段與節點屬性表中的NodeID字段關聯。為了模擬路網的動態性，采用時間離散化方法對路段擁堵系數進行每隔5 min的變化處理，結合路段長度以及通暢時路段速度求解路段行駛時間。本文采用的福州市部分路網數據共包含3 757個節點（包括轉向時延節點和轉向非時延節點），5 981個路段（包括單向路段和雙向路段），228個時段的擁堵系數。

鄰接矩陣和鄰接鏈表是路網資料常用的兩種存儲結構，由于城市有向路網的大規模性和稀疏性，采用鄰接矩陣表達路網數據需要消耗大量存儲空間與搜索時間，而鄰接鏈表充分利用了路網中路段的鄰接特性進行存儲，存儲空間和搜索時間的消耗均遠遠小于鄰接矩陣。因此，本文選用鄰接鏈表數據結構，在.NET平臺下，利用ArcEngine組件庫進行仿真實驗。

4.2 結果分析

種群規模是遺傳算法的一個重要參數，對求解精度和求解效率都存在較大影響，如圖3顯示了種群規模與收斂適應值、收斂代數的關系：當種群規模較小時，需要較多收斂代數，同時求解的收斂適應值較大不能滿足路徑規劃的精度要求；隨著種群規模增大，收斂次數減少，同時求解的收斂適應值逐漸減低，最終收斂次數和收斂適應值趨于平穩；當種群規模為20～60時，收斂適應值和收斂代數皆滿足最優路徑規劃的精度要求，但隨著種群規模的增加，同樣的收斂代數，種群規模越小，收斂計算時間越少。通過多次模擬分析，綜合考慮求解精度和效率，本文設定種群規模為30，交叉率為0.9，變異率為0.05，迭代終止條件為最優適應值連續5代保持不變或達到最大迭代次數100。

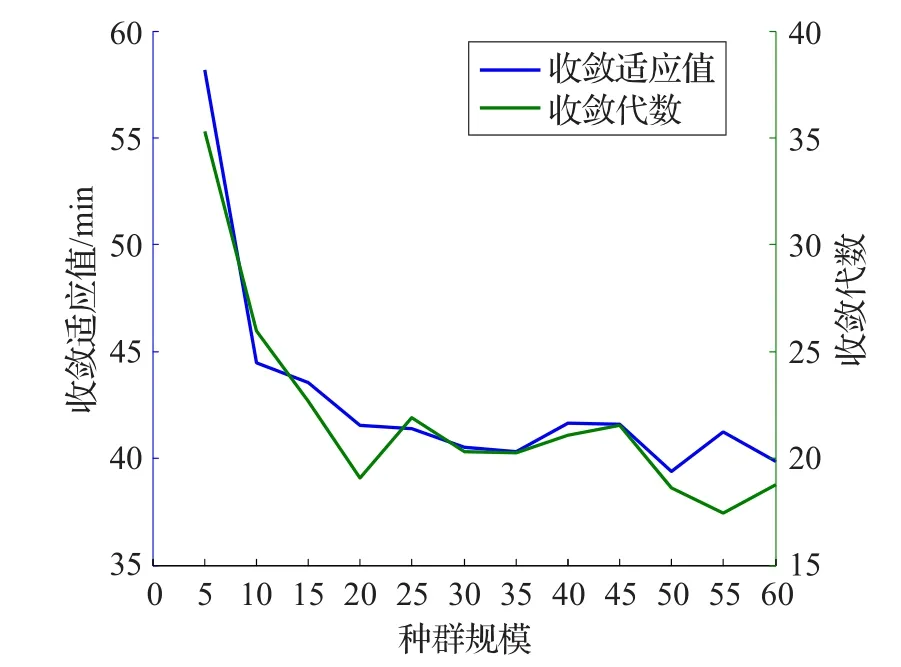
圖3 種群規模對收斂適應值和收斂代數影響

為便于比較分析算法的性能，選取傳統遺傳算法（GA）、文獻[22]中基于模擬退火的混合遺傳算法（SAGA），以及本文改進的遺傳算法（IGA）進行實驗對比，隨機選取一對OD點對，同時進行100代進化操作實驗，分析對比進化過程中每代種群中最優適應值的變化情況。如圖4所示，IGA在進化至13代時已達到收斂適應值，求解收斂速度快于GA和SAGA，同時IGA所求得的收斂適應值明顯優于GA和SAGA。分析可知，本文所采用的局部搜索策略通過利用鄰接節點自身的先驗知識，構建節點適應度，然后根據各節點選擇概率進行搜索，強化了局部搜索的目的性，進化過程中每一代種群最優值都有所提高，直至達到收斂適應值，從而提高了算法的局部搜索能力，使其具有更好的收斂性。

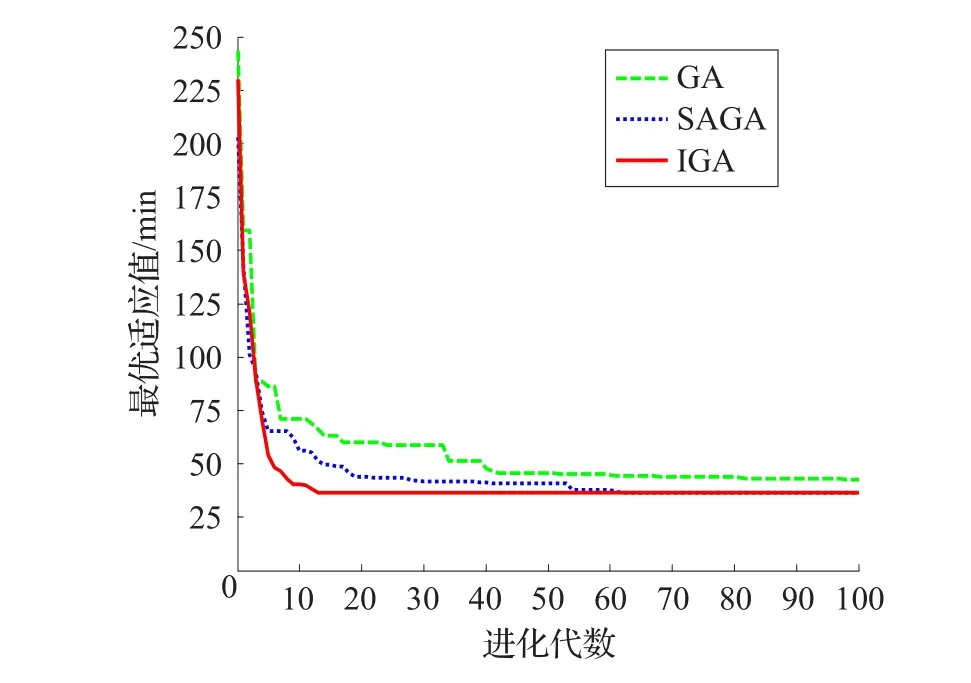
圖4 進化過程中最優適應值變化

進一步對該OD點對進行20次實驗，并利用第100代最優適應值的均值對之前每一代種群中最優適應值的均值做標準化處理，其值越趨近于1對應路徑越優，結果如圖5。IGA在前20代中具有很快的收斂速度，在進化至20代左右時的標準化適應值已達到0.9，即20次實驗中有若干次已十分逼近收斂結果，而GA和SAGA進化緩慢，直到40代之后才達到0.9，說明本文提出的改進算法IGA的收斂性和穩定性均優于GA和SAGA。

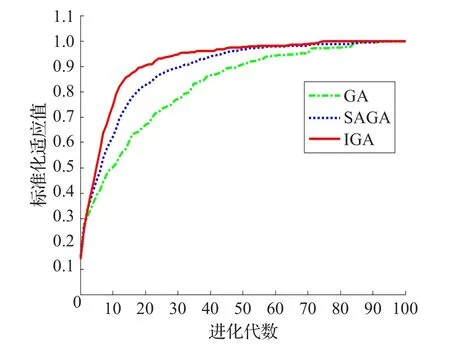
圖5 進化過程中標準化適應值變化

為避免偶然性，選取10對OD點對分別進行20次實驗，實驗結果如表1。精度上：IGA搜索到的最優個體所對應路徑的行程時間更少，相較于GA縮短約38%，相較于SAGA縮短約6%；效率上：IGA收斂時所需計算時間平均值為1.232 s，相較于GA降低約30%，比SAGA降低約20%。本文提出的算法IGA具有更好的局部搜索能力，求解精度和求解效率均有明顯提升，能更好地滿足動態路徑規劃需求。

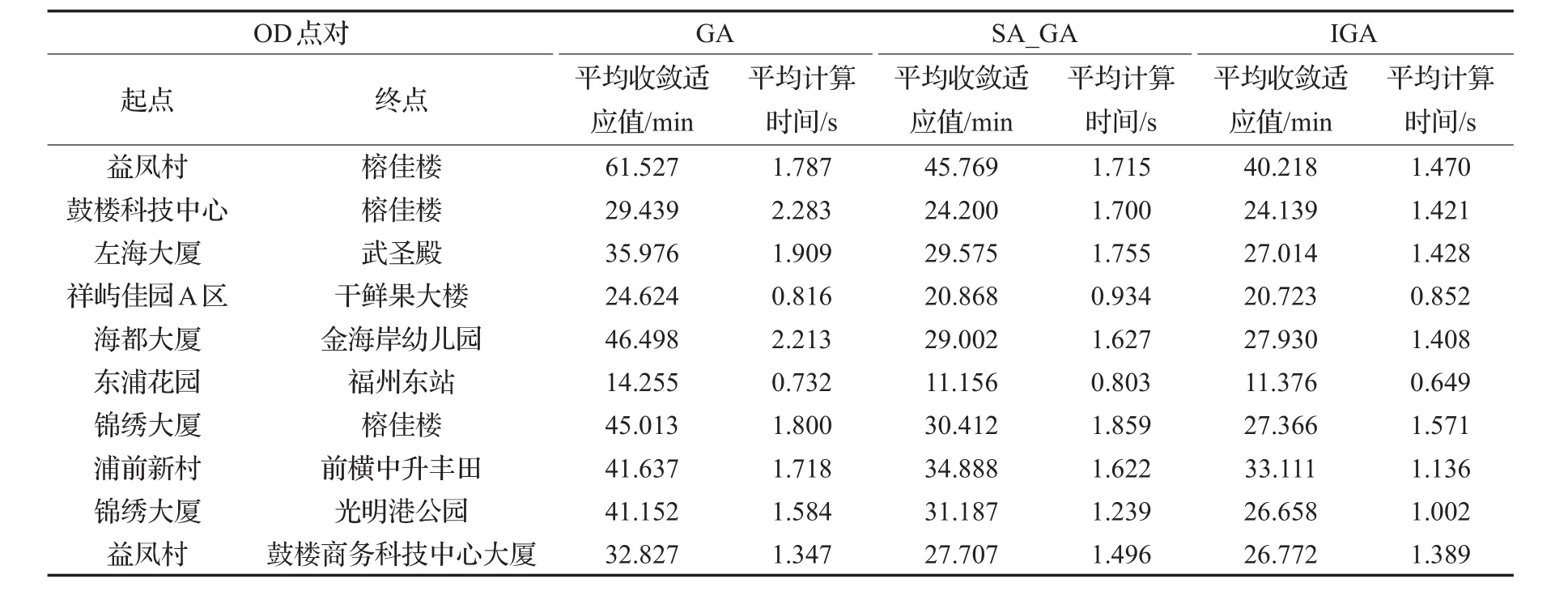
表1 不同OD點對實驗結果

為檢驗本文提出的算法的動態性與優越性，選擇錦繡大廈為起點，光明港公園為終點，采用三種算法分別進行動態路徑規劃誘導，結果如圖6、7、8所示，其中紅色代表擁堵路段，黃色代表擁擠路段，淡綠色代表較通暢路段，綠色代表通暢路段。初始時刻IGA所規劃的最優路徑避免不必要的轉向等次優行駛決策，具有更好的局部搜索效果，行程時間為19.69 min，優于GA的34.68 min，和SAGA的22.56 min；5 min后規劃路徑中剩余部分未出現擁堵路段，不需要重新進行路徑規劃；10 min后規劃路徑中剩余部分出現擁堵路段，重新規劃后得到規避了擁堵路段的新路徑。對比可知，本文提出的算法IGA能更好地處理動態路徑規劃問題。

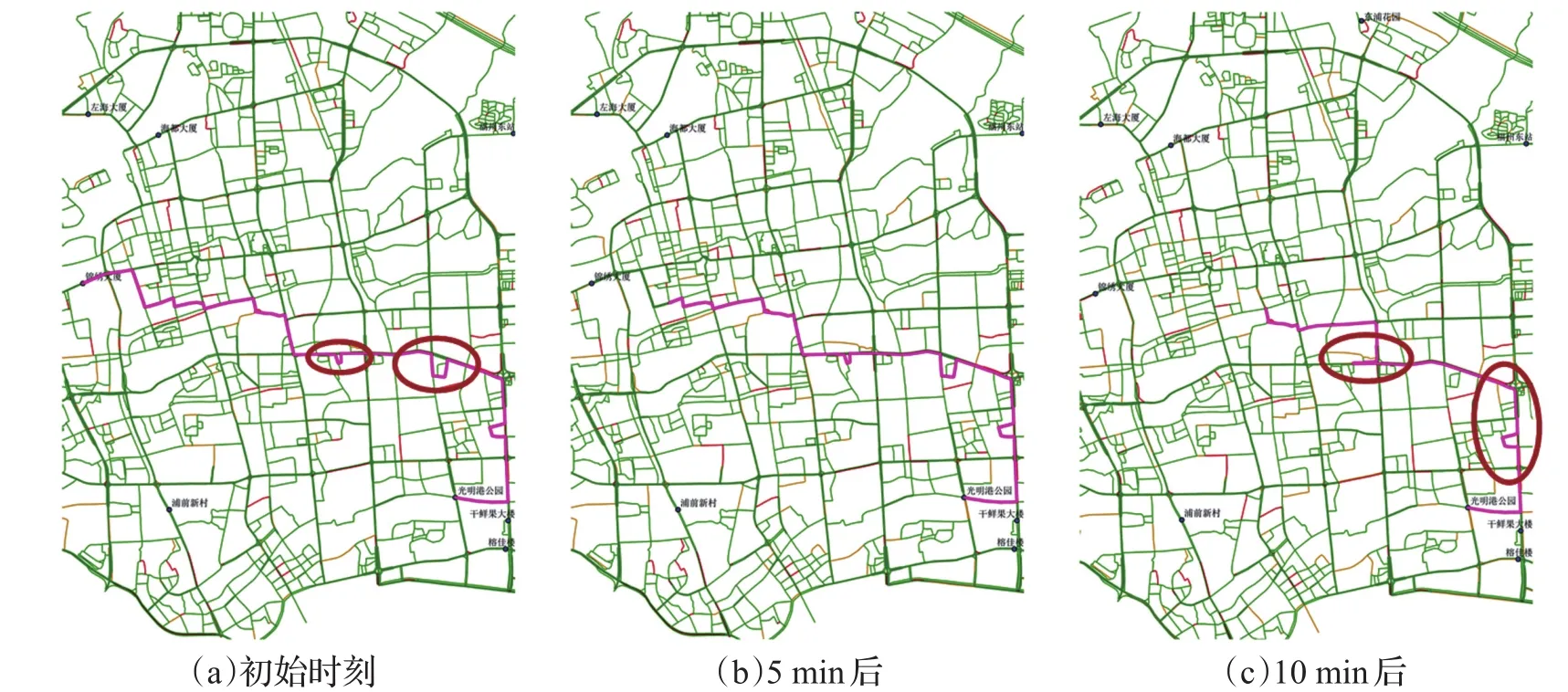
圖6 GA動態路徑規劃

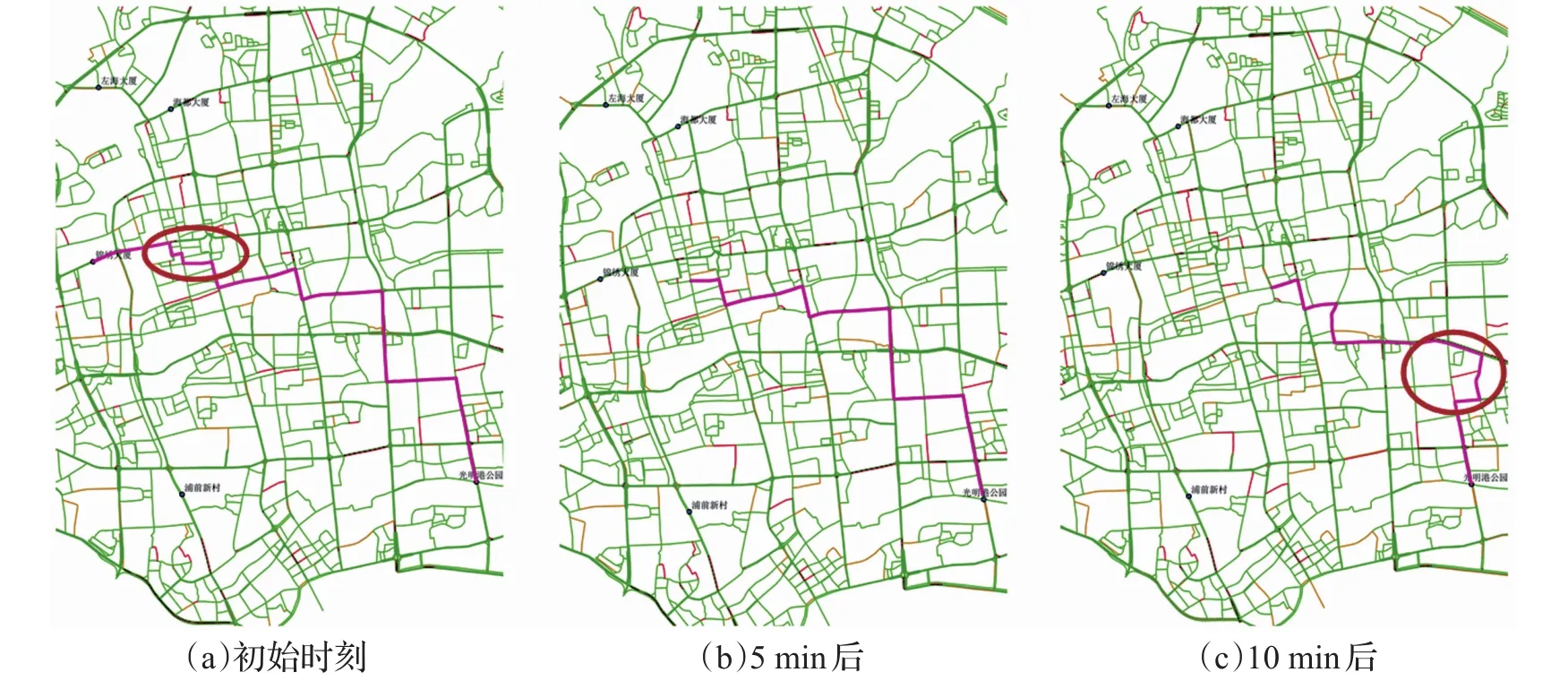
圖7 SAGA動態路徑規劃

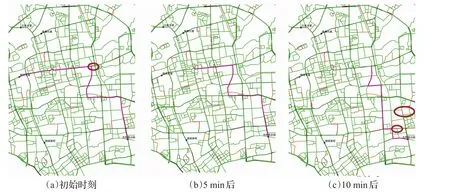
圖8 IGA動態路徑規劃

5 結論

本文針對城市路網中動態路徑規劃問題，提出一種改進的遺傳算法，該算法采用啟發式策略控制全局搜索方向確定初始種群；采用空間鄰近交叉策略完成交叉操作；使用前向、逆向的多向變異和重新生成新個體變異相結合的變異策略實施變異操作；引入節點選擇概率的局部搜索策略進行局部搜索，能有效克服傳統遺傳算法存在的“早熟收斂”，局部搜索能力差等問題，同時有著更高的收斂效率與更穩定的收斂性。實驗結果表明，提出的算法在搜索最優路徑的過程中具有更優的局部搜索能力，能有效地規避交通擁堵路段，滿足行進中的動態最優路徑規劃對求解精度和效率的要求。