基于人工魚群算法的波浪發電系統最優負載*

鄒子君，楊俊華，楊金明，王子為

(1.廣東工業大學 自動化學院，廣州 510006； 2.華南理工大學 電力學院，廣州 510641)

0 引 言

最大波浪能捕獲是波浪發電研究的關鍵技術，為提升波浪發電系統的平均輸出功率，已涌現各種控制方案。文獻[1]提出了一種變步長擾動觀察法，用于實現浮標式波能轉換裝置的最大功率點跟蹤。算法根據輸入功率的數值范圍，決定相應的變步長規則，緩解了算法跟蹤速度與精度的矛盾。仿真表明，該算法減少了裝置的輸出功率值與理論最大值間的穩態誤差，提高了裝置對不同波浪環境的適應性。但擾動觀察法的固有缺陷—最大功率點附近的功率振蕩會影響裝置的穩定性。針對振蕩水柱式波能轉換裝置，文獻[2]提出一種最大捕獲寬度跟蹤控制器(MCWT)，與傳統鎖存時間固定的控制器不同，該控制器可根據實際海浪條件自適應調節鎖存時間長度。同時，MCWT控制器的設計過程不需要系統的數學模型，假設條件與海浪條件差異不會影響實際控制效果。仿真表明，MCWT控制器可提高隨機波浪條件下裝置的魯棒性，增加波浪能捕獲功率值。但MCWT控制器需要傳感器測量波幅和波能轉換裝置的功率，實現成本較高。

為實現液壓動力輸出波能轉換裝置的最大波浪能捕獲，文獻[3]提出分離控制方案，基于龐特里亞金最大值原理設計控制率。仿真表明，與偽連續控制相比，分離控制能夠增加規則波下轉換裝置的波浪能捕獲寬度，不規則波浪條件下的輸出功率平均值也提高了47%。但該方法需提供波浪激勵力的預測值，在實際中不易實現。與典型的浮標式波能轉換裝置不同，可調傾角油壓動力輸出波能轉換裝置(ASAWEC)能夠從波浪的起伏運動和浪涌中捕獲波浪能量，為實現該裝置的輸出功率最大化，文獻[4]提出了學習向量定量神經網絡控制算法。通過數據集訓練神經網絡控制器，分類不同波形條件所對應的最佳傾斜角度，采用PI控制器，可在2 s內將裝置傾斜角調節至最佳值，實現輸出能量最大化。該算法有效性已得到規則波和不規則波條件下的仿真驗證，實際海浪條件的適用性有待進一步研究。

模型自由控制策略(MFC)，不依賴于控制對象的數學模型，特別適于波浪發電類難以建立精確數學模型且實際動態性能復雜未知的系統。為優化單體波浪能轉換裝置振蕩控制，文獻[5]采用MFC策略，能夠實現浮子速度與最佳速度跟蹤誤差的最小化，將輸出功率的峰均比從11.7大幅降至6.8，增加輸出功率平均值。并對參數不確定性、外部干擾等具有魯棒性，可將這些不確定因素造成的功率降幅減少一半。實際控制效果有待實際實驗驗證。

針對阿基米德擺式永磁同步直線波浪發電系統，文獻[6]提出了無速度傳感器控制，通過無跡卡爾曼濾波器估計直線發電機動子速度，從電機瞬時輸出有功功率獲得與波浪頻率匹配的最佳速度值，采用PI控制器跟蹤該最佳值，從而滿足Falnes提出的相位條件[7]，最大限度捕獲波浪能。

為優化波能轉換裝置的功率控制，文獻[8]提出了分層控制方案，通過求解浮子振蕩幅度約束條件下的最大吸收功率，產生參考速度。采用滑模變控制方法，調節浮子實際振蕩速度跟蹤最佳速度。仿真結果表明，與模糊控制、反應式控制相比，分層控制可提高裝置對非線性因素、擾動的魯棒性。但由于不規則波浪條件下產生的參考速度是對應波峰頻率的，分層控制只能是一種次優控制。

通過優化算法求解波浪發電系統的最優負載，是一種實現最大波浪能捕獲的有效途徑。傳統粒子群算法易使波浪發電系統負載值陷入局部最優，文中提出一種基于動物行為的人工魚群智能優化新算法，該算法已應用到微網可再生能源調度優化[9]、不均勻光照下光伏發電系統的MPPT控制[10]等問題中。通過比較“追尾或覓食或隨機”和“聚群或覓食或隨機”兩種組合行為得到的下一位置目標函數值大小，確定搜索方向，可增加搜索過程的靈活性。仿真結果表明，該算法可大幅增加波浪發電系統的平均輸出功率。

1 浮子的運動方程

圖1給出了振蕩浮子式波浪發電系統結構圖。

圖1 振蕩浮子式波浪發電系統結構圖

結構由浮子、直線發電機、電力電子變換器、儲能單元等模塊組成。浮子在波浪中運動時，不僅會引起阻尼力，還會受到重力和靜水壓力聯合作用引起的靜水恢復力的作用。根據波浪理論[11]，靜水恢復力及阻尼力的表達式為：

(1)

式中Fs(t)是靜水恢復力；Fr(t)為阻尼力；Ks是恢復力剛性系數；Rr是阻尼力阻尼系數；x為垂直方向上浮子偏離平衡位置的位移；t為時間。

浮子隨波浪振蕩時會產生輻射波，輻射波與海水相互作用會產生輻射力，可將輻射力表示為輻射阻抗與速度的乘積[11]：

(2)

式中FR(t)是輻射力；RR是因輻射力產生的附加阻尼；XR是因輻射力產生的附加電抗。

由牛頓力學，可得浮子的運動方程[11]：

(3)

式中m為浮子質量；Fex(t)為海浪激勵力，表示入射波作用于浮子上的力。

將上述Fs(t)、FR(t)、Fr(t)的表達式代入式(3)，可得：

(4)

整理后得：

(5)

對式(5)進行傅里葉變換，可得：

(6)

將s=jω代入式(6)，可得：

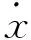
(7)

通常將附加電抗表示為[11]：

(8)

式中mR是因輻射力產生的附加質量。

將式(8)代入式(7)，可得：

(9)

變換式(9)，得到：

(10)

2 系統平均輸出功率的分析

系統輸出的平均功率為[11]：

(11)

從式(10)可得：

4）加強田間管理。重視提高麥田溝廂質量，降低田間含水量，為小麥根系發育創造良好的土壤環境，增強小麥自身的抗倒伏能力。根據植保情報，做好小麥病害綜合防治工作。

(12)

將式(12)平方后，代入式(11)：

(13)

式中在一定頻率下，參數Fex(ω)、ω、RR、Ks、mR、m均為常數，因此可對式(13)進行標么化處理，得：

(14)

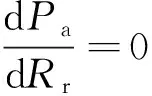
圖2 波浪發電系統輸出平均功率的曲線圖

對Pa的表達式，即式(13)求導可得：

(ωm+ωmR-Ks/ω)2]-2Rr(Rr+RR)=0

(15)

求解后可知Rropt的表達式為：

(16)

將式(16)代入式(13)，可得Pa的理論最大值:

(17)

式中的海浪激勵力Fex頻率與波浪運動頻率保持一致[12]，因此一定頻率下Fex的數值是固定的。從圖2可知，不同頻率下的最大功率點對應著唯一的一個Rr。于是，為尋求波浪發電系統的最優負載，增加輸出功率平均值，可利用人工魚群算法的尋優能力，通過迭代計算，迅速找到不同頻率下的Rropt，使Pa與Fex的比值滿足：

(18)

即可實現不同頻率下系統輸出功率最大化。

3 人工魚群算法

人工魚群算法是一種基于動物行為的群體智能優化算法，通過模擬魚群的覓食、追尾、隨機、聚群等行為在搜索域中進行尋優，求解優化問題。應用于波浪發電系統的最優負載求解問題，收斂速度快并具有取得全局極值能力。

首先，創建初始人工魚群。設定生成100條人工魚，隨機初始化個體位置。

然后，計算當前個體位置的目標函數值。比較“追尾或覓食或隨機”和“聚群或覓食或隨機”兩種組合行為得到的下一位置目標函數值的大小，選取較優的一種行為來執行，從而確定搜索方向。同時采用隨機移動步長，更新人工魚位置，并計算更新后的目標函數值。待所有個體均完成移動后，將每次迭代得到的最優人工魚位置及其對應的目標函數值存在bestx和besty。

最后，判斷當前迭代次數加1后是否大于文中的最大迭代次數500，若大于則停止搜索，輸出最優解；否則繼續上述的迭代過程。

圖3 第i條人工魚的追尾行為

圖4 第i條人工魚的覓食行為

圖5 第i條人工魚的聚群行為

4 仿真結果及分析

為驗證人工魚群算法的有效性，在Matlab/ Simulink仿真環境中結合小型波浪發電系統的數學模型，運行了人工魚群算法程序,如圖6所示。主要參數為：浮子質量m=45 kg，附加質量mR=0 kg，輻射力阻尼系數RR=300 N·S/m，剛性系數Ks=800 N·S/m。

圖6 人工魚群算法的流程圖

圖7～圖9分別是波浪周期T為5 s、6 s和7 s時，運行人工魚群算法和傳統粒子群算法的目標值優化過程，以圖7為例進行說明。圖7(a)為人工魚群算法的優化過程曲線，圖7(b)為魚群算法迭代500次的最優人工魚分布情況，圖7(c)為傳統粒子群算法的迭代過程。由圖7(a)、圖7 (b)的迭代次數可知，人工魚群算法在迭代到第2代的時候，目標值已基本達到最優解，而傳統粒子群算法需進化到第8代，始才逐漸穩定。因此，在成功尋優的迭代次數上，人工魚群算法的尋優速度更快。

圖7 周期為5 s時兩種算法的目標值優化過程

圖8 周期為6 s時兩種算法目標值的優化過程

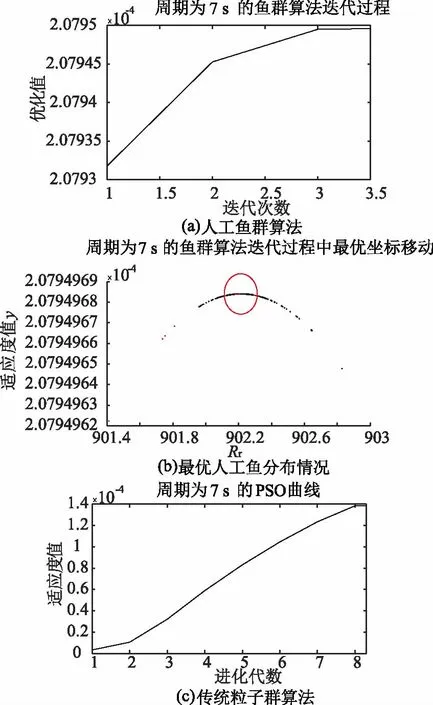
圖9 周期為7 s時兩種算法目標值的優化過程

表1和表2分別為采用人工魚群算法和傳統粒子群算法計算的目標值及與理論值的誤差。由此可見，與傳統粒子群算法相比，人工魚群算法所計算的目標值基本與理論值相等，可大幅增加波浪發電系統的平均輸出功率。

表1 采用人工魚群算法計算的目標值

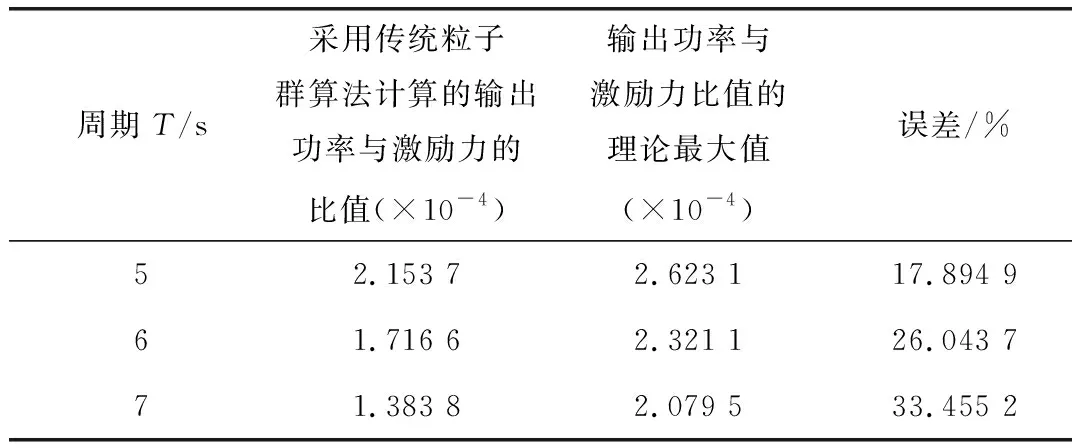
表2 采用傳統粒子群算法計算的目標值

5 結束語

人工魚群算法應用于尋找波浪發電系統的最優負載，可通過比較“追尾或覓食或隨機”和“聚群或覓食或隨機”兩種組合行為得到的下一位置目標函數值的大小，選取較優的一種行為來執行，從而確定搜索方向，可避免陷入局部最優，提高算法全局搜索能力。通過加入隨機移動步長，更新人工魚位置并計算更新后的目標函數值，求解優化問題。仿真結果表明，與傳統粒子群算法相比，所提算法尋優速度快，運行結果可達到理論最大值，獲得全局最優解，大幅增加波浪發電系統平均輸出功率，求解不同頻率下系統最優負載。