電力線信道系統噪聲的建模方法研究*

胡蘇陽，王莉，楊善水

(南京航空航天大學 自動化學院， 南京 211106)

0 引 言

復雜大系統(飛機、航空航天系統、核及可再生能源系統)的飛速發展促使電力線的使用日益增多，結構交錯密布，實際電力線信道具有衰減大、噪聲嚴重的問題[1-3]，對信息傳輸和故障診斷有較大干擾。因此對電力線信道傳輸特性建模研究引起國內外學者的廣泛關注[4-6]，在現有電力線系統噪聲建模研究中[7-10]，信道噪聲普遍采用傳統分類，主要包括有色噪聲、窄帶噪聲、脈沖噪聲[4]。然而實際航空電纜中電弧故障已成為普遍現象，給電網帶來高度非線性、時變性以及不可預測性的電弧噪聲，導致飛機配電網電壓畸變等問題，這給航空航天系統的可靠工作以及電力線故障的準確檢測定位帶來極大挑戰；且電氣系統中的電弧故障可能會中斷電源供電、損壞電力設備、引起火災甚至威脅人類生命安全。因此亟需建立適應多條件的、更加全面、準確的電弧噪聲模型，將電弧噪聲與典型電力線噪聲相結合，進一步完善電力線信道噪聲特征，建立更加全面的電力線系統信道模型。

1994年，意大利博洛尼亞大學的Montanari G C等學者將電弧電壓定義為電弧長度的函數，弧長的時變性通過疊加帶通白噪聲得到[11]； 1996年，美國克萊姆森大學的Srinivas Varadan等學者通過簡化電弧爐負載u-i特性曲線得到電弧電壓表達式[12]，將帶通白噪聲疊加于電弧電阻上模擬負載電阻的時變性； 2008年，上海交大的王育飛，潘艷霞[13]等通過直接疊加帶通白噪聲于確定性電弧電壓上，得到用于電壓波動與閃變研究的電弧爐隨機模型。但以上模型建模較復雜，只能適用于特定的環境。當外界環境改變時，需要專業人員重新考慮方程的合理性，其通用性有待提高。

文中主要研究內容如下：首先對典型電力線噪聲進行分類并分析其不同特性，建立典型電力線噪聲模型；然后結合實驗平臺中采集得到的電弧數據，提出基于分數階濾波器的電弧噪聲建模方法以及基于數據驅動的電弧噪聲模型參數確定方法；最后通過仿真和實驗結果驗證模型的準確性。

1 電纜信道噪聲特性仿真與分析

電纜信道環境中的噪聲按大類可分為有色背景噪聲、窄帶噪聲、脈沖噪聲[14](包括工頻異步周期脈沖噪聲、工頻同步周期脈沖噪聲等)，其中還包括一些復雜電氣現象帶來的復合噪聲，如電弧噪聲，呈現高度不確定性與隨機性，文中基于Matlab對這些噪聲特性進行分析并建模。

1.1 典型電纜信道噪聲

1.1.1 有色噪聲

有色背景噪聲來自各種低功率噪聲源，如電腦，調光器等，其頻譜較寬且持續存在。從時域角度來看，有色背景噪聲的產生過程，即白噪聲信號w(n)通過一個特定的濾波器H(z)得到輸出的有色背景噪聲x(n)。

噪聲整形濾波器模型的傳遞函數如下所示：

(1)

式中函數的分母A(z)表示的是自回歸AR部分；ai和p是濾波器的系數和階數，將典型白噪聲序列通過線性穩定濾波系統H(z)，即能表示出噪聲的產生過程。

1.1.2 窄帶噪聲

窄帶噪聲通常由調制的正弦波疊加而成，主要由中短波廣播等無線信號在電力線信道中引起的串擾而產生，其頻帶較窄，可通過式(2)所示的N個獨立的正弦函數疊加生成。

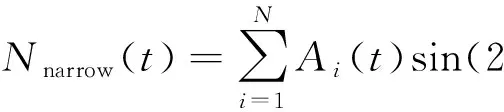
(2)

式中Ai(t)是對信號近似的調制幅值；φi表示相位，在0～2π之間隨機產生；fi為各正弦信號頻率。

1.1.3 工頻同步的周期脈沖噪聲

工頻同步的周期脈沖噪聲主要由整流器件產生，伴隨高能量高次諧波，整流器件在每個工頻周期內產生兩次沖擊電壓，導通一次，截止一次，重復頻率為50 Hz或100 Hz。其特點是持續時間短，脈沖強度高于背景噪聲。電纜上的脈沖噪聲可以由衰減的正弦波疊加而成，文中采用指數規律衰減的正弦信號來表示，考慮到整個時間軸上脈沖出現的時間，時間軸上所有工頻同步周期脈沖噪聲可表示為:

(3)

式中A為脈沖幅度0～45 dB；l為整流器件沖擊電壓的個數；tarr為單個脈沖出現時間；f為衰減正弦波頻率，脈沖周期為0.02 s，脈沖寬度τ由整流器件導通或截止時間決定。

1.1.4 工頻異步的周期脈沖噪聲

工頻異步的周期脈沖噪聲主要來源于計算機顯示器的掃描諧波等，與工頻同步周期脈沖噪聲不同的是，其出現頻率由顯示器的掃描頻率決定。文中工頻異步脈沖噪聲采用指數規律衰減的正弦信號疊加產生，可表示為：

(4)

1.2 電纜信道電弧噪聲

電弧是指由于電場過強，氣體發生電崩潰而持續形成等離子體，使得電流通過通常狀態下的絕緣介質(例如空氣)的現象。當電弧產生并穩定燃燒后，電弧電流中還存在著電弧電流交流分量，該交流分量分布不具有周期性，呈現為一種噪聲的特性，該噪聲主要來源于電弧陰極鞘層區的射頻信號[15]。

對電弧噪聲特征的建模首先需要利用電弧模擬發生裝置對故障進行模擬，并準確采集電弧電流、電弧電壓、電弧電流交流分量等電氣特征量，分析其時域及頻域特征。圖1所示為電弧故障模擬、測試自動化研究平臺。

圖1 電弧故障模擬、測試自動化研究平臺實物圖

使用銅作為陰極、碳作為陽極，輸入電壓恒定為270 V，27 Ω電阻作為負載，利用電動電弧發生器產生不同弧長的電弧。采集電弧電流交流分量進行FFT分析，頻譜圖如圖2所示，從圖中可以看出隨著弧長的增大，在低頻段電弧電流頻譜幅值不斷的增加，呈現為不同衰減速率的有色噪聲。

圖2 電弧噪聲諧波頻譜隨弧長變化對比圖

根據圖2中分析的特性，電弧噪聲分為兩個頻帶，分別為幅值隨頻率增加而衰減的低頻帶，近似于有色噪聲；幅值基本保持不變的高頻帶，近似白噪聲。文中基于Matlab，利用白噪聲模塊產生隨機噪聲，并設計濾波器，基于建立實際情況相符的電弧噪聲模型。

1.2.1 基于分數階濾波器的電弧噪聲建模方法

采用單極點單零點的PI補償網絡設計濾波器，濾波器的傳遞函數為：

(5)

需要利用分數階微積分的思想，構造滿足指定傳遞函數的濾波器，以調整幅值衰減的速率，用一個有限的整數階微分方程來近似描述分數階系統。對于形如G(s)=su,α∈(0,1)的傳遞函數，使用分數階的方法步驟如下：

(1)給定需要等效的近似頻段的范圍[1/v,v]，及近似的階次M。近似階次M越大，擬合效果越好，但計算量會大大增加。實驗表明，階次M通常取4時，得出的結果以及各方面因素是令人滿意的，因此，文中采用近似階次M=4；

(6)

(7)

K=v-u

(8)

(3)由式(9)計算出分數階傳遞函數G(s)=su的等效整數階有理傳遞函數形式：

(9)

在得到分數階傳遞函數后，還需要對白噪聲進行放大或縮小一定的倍數w，所以最終的傳遞函數表達式為：

(10)

該方法中的分數階濾波器的參數需要確定，包括濾波器的階次u、濾波器截止角頻率v，放大倍數w。這三個參數是為了擬合電弧噪聲特性而提出的，并無實際的物理意義，只能通過人工反復調整參數實現仿真與試驗波形的吻合。而這種方式只能反映單次試驗時的電弧噪聲隨機性特征，當電弧發生條件改變時，需要重新確定參數，不具有通用性。

1.2.2 基于數據驅動的電弧噪聲模型參數確定方法

數據驅動方法能夠通過分析研究對象的數據，分析系統變量的內部邏輯關系，離線或在線學習計算與當前狀態下匹配的模型數據。提出使用數據驅動的方法確定故障電弧隨機性噪聲模型中的參數，采用離線數據計算不同工作條件下參數的變化。

對于每一次試驗采得的數據，均需要待定電弧隨機性模型的參數：濾波器的階次u、濾波器截止角頻率v，放大倍數w。因此，采用遍歷法對每一個參量進行遴選，以使得擬合得到的頻譜結果與實驗結果最接近。為了能夠定量評定擬合的效果，采用電流在低頻段(0～50 kHz)的諧波幅值和判斷濾波器的階次u、濾波器截止角頻率v擬合效果，采用電流在高頻段(200 kHz ～500 kHz)的諧波幅值和判斷放大倍數w。

具體的步驟如下：

(1)讀入實驗數據，對其進行FFT分析，計算得到試驗數據的低頻段和高頻段諧波幅值和；

(2)設定濾波器的階次u、濾波器截止角頻率v，放大倍數w的初值；

(3)利用上文中的方法，計算得到分數階濾波器的表達式；

(4)使用分數階濾波器對N(0,1)的白噪聲進行濾波，并對濾波后的波形進行FFT分析，計算得到仿真數據的諧波幅值和；

(5)計算試驗數據與仿真數據的諧波幅值和之間的誤差；

(6)將誤差與誤差最小值相比，當誤差大于最小誤差時，更新最小誤差，并記錄下此時的u,v,w；

(7)重復步驟(2)～步驟(6)直至遍歷所有的u,v,w值后結束循環，輸出此次試驗下，誤差最小時的u,v,w。

對電弧電流交流分量離線數據進行擬合，獲得的電弧噪聲模型擬合頻譜結果如圖3所示。

圖3 電流6 A弧長11 mm的電弧噪聲模型擬合頻譜

2 電纜信道系統噪聲模型實驗驗證

利用圖1所示電弧故障模擬、測試自動化研究平臺對電力線信道噪聲模型進行實驗驗證。擬合電弧噪聲與實測數據的頻譜對比圖如圖4所示，電弧噪聲諧波的仿真波形與實驗波形基本契合，在4 Hz～2 kHz頻段內呈現有色噪聲的特性，在2 kHz～500 kHz頻段內呈現出白噪聲的特性，能夠較好的還原電弧噪聲諧波分量的頻域信息。

圖4 電流6 A、弧長11 mm的電弧噪聲模型與實測數據頻譜圖對比

求取相同弧長、不同電流時的諧波幅值和如圖5所示，□和○分別表示實驗和仿真獲得的頻域特征平均值結果。從圖中可以看出，實驗結果與仿真結果的頻域特征量統計區域較為吻合，計算得統計平均誤差為15.3%。

圖5 不同電流下1mm弧長電弧噪聲頻域特征

為了驗證模型對外界條件變化的適應程度，比較電極改變時電弧電流的時域特征，采用碳為陰極，銅為陽極，同樣比較相同電流(20 A)不同弧長的頻域特征量，如圖6所示，□和○分別表示實驗和仿真獲得的頻域特征平均值。在電弧弧長小于15 mm時，此時實驗結果與仿真結果的頻域特征量誤差較小，統計平均誤差為5.7%。而當電弧弧長大于15 mm時，實驗結果頻域特征量隨弧長增大而減小，仿真結果則基本維持不變，此時擬合誤差稍大，統計平均誤差為25.8%。

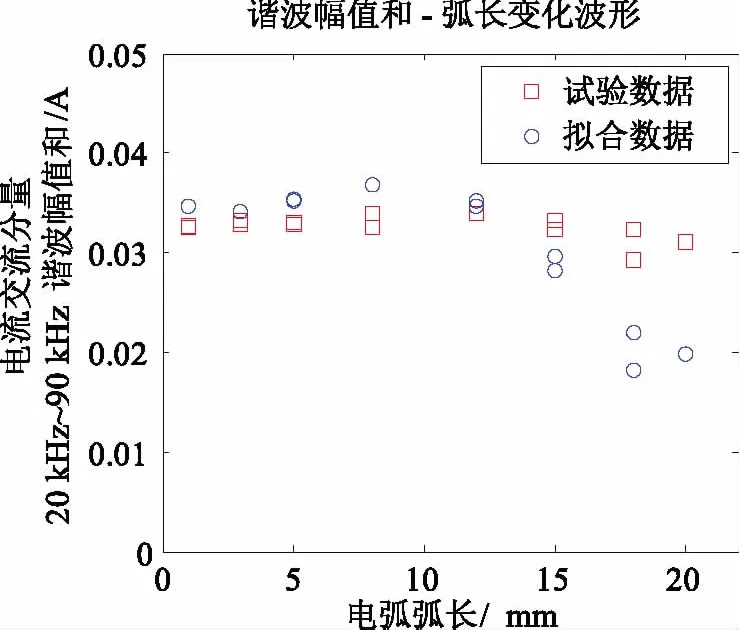
圖6 不同弧長下20 A電弧電流頻域特征

對電力線中的窄帶噪聲模型與實驗數據的時頻域對比如圖7所示。

圖7 窄帶噪聲模型與實測對比圖

對電力線中工頻同步脈沖噪聲模型與實驗數據的時域對比如圖8所示。

圖8 工頻同步脈沖噪聲模型與實測對比圖

對電力線中工頻異步脈沖噪聲模型與實驗數據的對比如圖9所示。

考慮到時域波形受電網環境隨機性的干擾誤差，噪聲模型對噪聲的時域、頻域特性的分布擬合較為準確，驗證了模型對典型電力線噪聲擬合的準確性。

圖9 工頻異步脈沖噪聲模型與實測對比圖

3 結束語

對電力線信道典型噪聲的不同特性進行分析，并提出基于分數階濾波器的電弧噪聲建模方法以及基于數據驅動的電弧噪聲模型參數確定方法，完善了電力線信道噪聲模型，通過理論分析、仿真和實驗驗證得到以下結論:

(1)電弧噪聲在4 Hz～2 kHz頻段內呈現有色噪聲的特性，在2 kHz～500 kHz頻段內呈現出白噪聲的特性；

(2)提出的電弧噪聲模型可以模擬不同電流、弧長條件下的電弧高頻噪聲特性。隨著電弧電流的增大，其高頻噪聲諧波幅值和具有先減小后增大的趨勢；

(3)在碳為陰極、銅為陽極時，在0～30 A狀態下對0～15 mm弧長電弧實驗結果擬合效果較好，在15 mm以上弧長狀態下，實驗結果頻域特征量隨弧長增大而減小;

(4)將典型電力線噪聲模型和所提出的電弧噪聲模型相結合，進一步建立了更加完善、準確的電力線信道系統噪聲模型，為后續開展電力線故障診斷技術的深入研究奠定了基礎。