棧式降噪自編碼網絡在變壓器故障診斷中的應用

許倩文，吉興全，張玉振，李軍，于永進

(1.山東科技大學 電氣與自動化工程學院，山東 青島 266590； 2.國網山東省電力公司威海供電公司，山東 威海264200)

0 引 言

變壓器是電力系統的核心設備，系統的安全性受其運行狀態的直接影響，準確診斷變壓器內部潛伏性故障對于保障電網安全運行具有十分重要的意義。變壓器狀態可通過其油中溶解氣體的含量與構成獲得基本了解。故而，油中溶解氣體成為變壓器故障診斷中的可靠依據之一。以油中溶解氣體分析(Dissolved Gas Analysis，DGA)為基礎形成了三比值法[1]、Rogers法[2]等傳統方法，以及反向傳播(Back Propagation，BP)神經網絡[3]、支持向量機(Support Vector Machine， SVM)[4-5]等人工智能方法。在實際運用中，發現三比值法，Rogers法等傳統方法對故障診斷有一定效果，但也存在編碼不全、判斷標準過于絕對等問題，反而不利于故障診斷；而BP神經網絡方法雖然特別適合于求解內部機制復雜的問題，但存在已出現震蕩、收斂速度低等不足；基于本質分析，SVM法為一類二分類算法。面對多分類問題，表現出分類效率低、不易構造學習器等劣勢；同時，上述方法均屬于淺層機器學習方法，這些方法均需依賴于完備且準確的樣本，方可獲得較為滿意的診斷結果，如此即不能充分借助變壓器油色譜實現對所得的眾多無標簽樣本在線監測目的。

提出的基于棧式降噪自編碼網絡(Stacked Denoise Auto-encoder，SDAE)的故障診斷方法，把深度學習應用于設備故障診斷，由無監督預訓練和有監督微調兩個階段構成，是一種半監督式的機器學習方法，該方法學習能力強，能夠給出變壓器各種運行狀態的概率。最后，通過工程實例來測試所構建的方法，同時與常規BP神經網絡方法進行對比分析。

1 棧式降噪自編碼模型

1.1 降噪自編碼網絡

自編碼器(Auto-Encoder，AE)是一種無監督學習的非線性特征提取模型。由編碼器和解碼器兩部分組成，結構如圖1所示。嘗試學習一個恒等函數，使輸出值接近輸入值。

圖1 自編碼器結構示意圖

降噪自編碼(Denoise Auto-Encoder， DAE)與自編碼的不同點體現在：前者原始輸入數據中增加了噪聲，接著以網絡輸入數據形式，對先前不含噪聲的輸出原始數據加以重構。故而，DAE的損失函數為構造網絡輸出和原始數據兩者的一個差異性度量。新增噪聲接著對原始數據加以訓練恢復，能夠提升網絡抗噪能力，從而增強自編碼的魯棒性。假設x是無噪聲的原始輸入，DAE首先利用一個隨機映射x′～qDx′|x把原始輸入數據x腐蝕為含有噪聲的數據x′。

編碼函數fθ把x映射到隱含層得到隱含層特征矢量y，函數表達如下：

y=fθx′=sWx′+b

(1)

式中s是編碼網絡的非線性激活函數，通常采用sigmoid函數；θ=W,b為編碼參數集合；W是m×n維權重矩陣；b是m維偏置向量。

再利用解碼函數gθ重構x得到z，函數表達式如下：

z=gθy=s′W′y+b′

(2)

式中s′是解碼網絡的激活函數；θ′=W′,b′為解碼參數集合；W′是n×m維解碼權重；b′是n維偏置向量。

最后通過不斷調整θ和θ′的值，去盡可能擬合為一個恒等函數，實現重構誤差的最小化。

重構誤差可表示為：

(3)

如圖2所示，DAE追求的是存在擾動的情況下對真實信號的重構能力，由此得到的特征表達具有更好的魯棒性和泛化能力。其中x表示原始輸入數據，x′表示加入噪聲的輸入數據，y為對x′進行編碼得到新的特征z為對y進行解碼后的輸出。

圖2 降噪自編碼器

1.2 棧式降噪自編碼網絡

棧式降噪自編碼網絡(Stacked Denoise Auto-Encoder，SDAE)是一個由多層DAE堆疊構成的深層神經網絡，其上一層DAE的輸出用于其下一層DAE的輸入，如圖3所示。棧式降噪自編碼神經網絡分為無監督預訓練和有監督微調兩個階段。

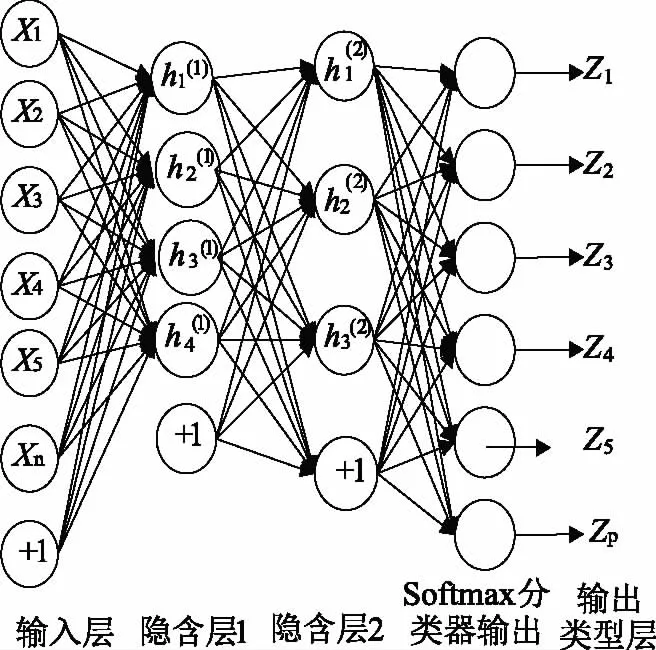
圖3 SDAE模型

(1)無監督預訓練階段。

該階段是采用逐層貪婪訓練法進行訓練。如圖3所示，每一個隱含層均與上一層構成一個DAE編碼網絡。然后利用反向傳播優化算法，求得每個DAE網絡代價函數取得最小值時的權重矩陣和偏置項，并通過不斷減小上述的代價函數值，當達到指定的迭代次數或者代價函數下降到指定值時，得到最佳的權重矩陣以及偏置項。

(2)有監督微調階段。

將預訓練步驟得到的編碼網絡的最佳權重矩陣和偏置，利用反向傳播算法再次迭代和更新各個權重矩陣和偏置項，直到達到最大的迭代次數,從而獲得每一層最終的最佳權重矩陣以及偏置項；在初步確定每個SDAE的隱含層數、每個隱含層的單元數以及學習率的情況下，將屬于同一種故障類型的訓練樣本集作為輸入，通過預訓練和微調來確定每個SDAE每一層最終的最佳權重矩陣和偏置項。

(3)分類輸出。

為實現變壓器故障的分類，微調時丟掉SDAE的“解碼”層，直接將Softmax分類器視為網絡的輸出層，把最后一個隱含層的輸出作為特征輸入到Softmax分類器進行分類。

2 基于SDAE的變壓器故障診斷方法

2.1 輸入向量的確定

從上述討論中可知，SDAE具有較強的樣本特征提取能力，選取H2、CH4、C2H2、C2H4、C2H6這5種特征氣體的體積百分數作為依據來判定變壓器的故障類型，將其作為網絡的輸入向量，由于這5種特征氣體含量值差別較大，為使網絡有良好的收斂性，將輸入數據進行歸一化處理，將所有輸入向量的取值處理在0～1之間。

2.2 輸出向量的確定

網絡的輸出對應變壓器的故障類型，將變壓器的狀態分為低溫過熱、中低溫過熱、中溫過熱，高溫過熱，低能放電，高能放電，以及正常這7類，狀態類型對應的編碼詳見表1。

2.3 變壓器故障診斷的SDAE網絡模型

圖4所示為診斷變壓器故障的SDAE網絡模型。此模型的輸入H2、CH4、C2H2、C2H4、C2H6這5種經歸一化分析的油內所含溶解特征氣體值，將變壓器各運行狀態相應的概率當做模型的輸出，其中故障診斷結果為具備最高概率值的狀態。

就變壓器故障診斷SDAE模型而言，其存在非監督預訓練、監督式微調這兩個訓練過程。前者主要通過大量預訓練樣本實現網絡底部各層DAE參數的初始化操作；后者是借助丟掉SDAE的“解碼”層，直接把最后一個隱含層的輸出作為特征輸入到Softmax分類器進行分類。

表1 變壓器狀態編碼

圖4 基于SDAE網絡的變壓器故障診斷模型

2.4 基于SDAE網絡變壓器故障診斷的步驟

(1)選取樣本數據和輸入向量；

(2)確定輸出向量，對變壓器狀態進行編碼；

(3)建立變壓器故障診斷SDAE網絡模型；

(4)利用SDAE網絡模型，對網絡的每一層進行參數初始化；

(5)采用逐層貪婪訓練法使用樣本數據依次訓練網絡每層的DAE，從而預訓練整個神經網絡；

(6)用完成分類標簽處理的樣本數據，借助BP算法，監督式訓練整個分類器，促進微調的進一步實現；

(7)丟掉SDAE的“解碼”層，直接把最后一個隱含層的輸出作為特征輸入到Softmax分類器實施分類；

(8)對已完成訓練的網絡加以保存，同時通過測試集樣本來測試網絡診斷性能。

3 算例分析

為驗證基于SDAE實現的深度神經網絡對變壓器故障診斷的效果，選用某供電公司提供的已確定實際故障結果的變壓器DGA數據，總共2 000組檢測記錄作為樣本，其中1 200組作為訓練數據，800組作為測試數據。其對應的7種故障類型如表2所示。文中SDAE具有兩隱含層的DAE，并采用多個分類輸出的Softmax作為分類器，用7位二進制編碼作為輸出。

表2 故障診斷樣本統計

為了分析降噪對故障診斷的影響，將SDAE深度網絡模型和未加噪的棧式自編碼深度網絡模型分別用于變壓器的故障診斷。兩種網絡模型用于相同訓練樣本和測試樣本，其它各個參數也相同。通過比較得出各個模型對變壓器故障診斷的影響如圖5所示。

圖5 診斷準確率

由圖5中可看出，加噪后的模型能使網絡整體的診斷準確率提高，加強了樣本在擾動狀況時所表現出的重構真實信號能力，進而促進特征表達泛化能力與魯棒性的提升。

為比較文中SDAE網絡模型的性能，分別采用三比值法，BP神經網絡和SVM對相同的樣本集進行訓練和故障診斷。各故障類型的診斷準確率如表3所示，表4則列舉了測試樣本集中10組典型樣本的診斷實例。

表3為三比值法、BP、SVM、SDAE分別對應測試樣本在各個故障類型診斷的準確率，從表3中可看出，三比值法的診斷準確率為78.2%，BP準確率為79.3%，SVM準確率為88.03%，SDAE準確率為95.2%。因而證明了所提出的SDAE方法與三比值法、BP、SVM相比，在變壓器故障診斷方面具有更高的準確率。

從表3、表4中進一步可得出：

表3 不同方法的診斷結果比值

表4 變壓器故障診斷實例

(1)SDAE與三比值法相比，較好的解決了三比值法中編碼不全、判斷標準過于絕對等問題，診斷準確率高于三比值法；

(2)SDAE與BP相比，診斷準確率更高，SDAE通過無監督預訓練和有監督調優兩個階段，實現高維深層故障特征的自適應提取和挖掘，改善BP神經網絡易陷入局部極小化和收斂速度慢的問題，此外，SDAE最后利用Softmax分類器，對故障進行分類輸出，提高了故障診斷的準確率；

(3)SDAE與SVM相比，SDAE中的Softmax分類器，可直接用于多分類情況。而基于本質分析，SVM屬于二分類算法。針對此算法分類效率低、不易構造學習器問題，SDAE算法做出了優化與彌補。

4 結術語

提出的基于SDAE模型用于變壓器故障診斷的技術，將深度學習推行到變壓器設備故障診斷領域。此項技術在腐蝕原始輸入數據的基礎上，自含有噪聲的輸入中掌握的特征在魯棒性上表現更佳；并且對照傳統機器學習方法，證明了該方法的有效性。所提出的故障診斷技術在故障準確率方面仍可進一步提高，可以在特征提取方面進行改善。