基于差分平面法的CT飽和檢測及補償研究*

林國營，宋強，潘峰，李開成，王凌云

(1.廣東電網有限責任公司電力科學研究院,廣州 510000； 2.華中科技大學 電氣與電子工程學院 強電磁工程與新技術國家重點實驗室，武漢 430074)

0 引 言

繼電保護系統的正常運行需要準確的電網電流數值。電力系統通過電流互感器測量電流的大小。當系統發生故障時，較大的故障電流可能導致電流互感器飽和，從而產生較大的電流測量誤差，引起電流差動保護等繼電保護系統的誤動[1-2]。使用羅氏線圈代替傳統的電磁式電流互感器是解決電流互感器飽和的有效方法，然而傳統電磁式電流互感器已經在電力系統中廣泛安裝使用。這要求繼電保護系統可以有效檢測、識別電流互感器飽和，從而防止誤動。

國內外的學者已經提出了眾多的電流互感器飽和檢測算法。有學者提出通過檢測電流互感器二次電流諧波含量來判斷是否發生飽和[3-4]。這種方法需要對電流信號進行傅里葉變換，至少需要一個周期的電流數據，實時性較差。

有學者利用線路虛擬阻抗在正常工況下不發生突變的原理來檢測互感器是否飽和[5-6]。然而該方法將受到電網阻抗模型及電壓信號的影響。有學者使用差分方程或數值求導對飽和區間進行檢測[7-9]。此類方法計算量小、實時性強，但在微弱飽和情況下檢測能力有限，且易受噪聲影響。

在檢測到互感器飽和后，學者使用相關的補償算法來對飽和畸變的二次電流進行校正。常用的互感器飽和補償算法有：基于人工神經網絡的補償算法、計算勵磁電流的補償算法、基于未飽和區間數據的補償算法等[10-13]。其中基于人工神經網絡的補償算法受訓練樣本的限制，不易于推廣應用。基于勵磁電流計算的補償算法通常基于互感器模型，需要電流互感器負載阻抗等相關參數。基于未飽和區間數據的補償算法通常利用最小二乘法等方法通過未飽和的電流數據對電流曲線進行擬合。然而該類方法需要先準確判斷互感器的進出飽和時刻。

為了解決上述算法存在的問題，提出了一種基于差分平面的電流互感器飽和檢測、補償新方法。該方法利用電流差分平面上各點的距離來檢測互感器飽和的飽和時刻。在檢測到飽和起始時刻后，使用改進的最小二乘擬合來對二次側畸變電流進行補償。該方法沒有使用復雜的數學工具，因而算法簡單、實時性強。PSCAD/EMTDC仿真證明該方法在電流互感器存在剩磁、不同負載等工況下均能有效實現電流互感器的飽和檢測及補償。

1 差分平面法

差分方程法是電流互感器飽和檢測的常用方法。設電流互感器二次側電流為i，則電流互感器二次電流的一至三階差分方程為：

id1n=in-in-1

(1)

id2n=in-2in-1+in-2

(2)

id3n=in-3in-1+3in-2-in-3

(3)

式中id1、id2和id3分別代表互感器二次電流的一階差分、二階差分和三階差分。

差分方程法通過將差分電流極值和閾值對比的方式來檢測電流互感器飽和。當電流互感器飽和較為微弱時，互感器飽和時刻的差分電流可能會小于所設定的閾值。為提高電流互感器飽和檢測能力，利用各階差分電流組成差分平面，如以二次電流i為橫坐標，一階差分id1為縱坐標，可組成i-id1差分平面。同理可使用id1、id2和id3組成id1-id2差分平面和id2-id3差分平面。當電網正常運行時，電網電流接近標準正弦信號，在各差分平面上電流軌跡為橢圓形，如圖1所示。

當系統發生故障時，故障電流可分解成幅值為If的穩態正弦分量以及時間常數為τ的直流衰減分量，故障電流如式(4)所示：

(4)

圖1 電網正常運行下的差分平面軌跡

由于采樣頻率遠小于直流衰減分量的時間常數，故直流分量的差分可近似忽略。當故障發生而電流互感器不飽和時，故障電流在各差分平面上的軌跡仍近似為橢圓形。圖2顯示了故障電流及其在各差分平面上的軌跡。由圖2可知當故障發生時，在i-id1差分平面上的電流軌跡受直流衰減分量影響較大，出現了多個橢圓。在id1-id2和id2-id3差分平面上，電流軌跡幾乎不受直流衰減分量的影響。

圖2 短路故障下的差分平面軌跡

差分次數越高，差分方程受直流衰減分量影響越小，但受噪聲的影響也越嚴重。id1-id2差分平面的抗噪聲能力強于id2-id3差分平面。當圖2中的故障電流疊加30 dB高斯白噪聲時，二次電流在各平面上的軌跡如圖3所示。由圖3可知，在30 dB噪聲環境下，id1-id2差分平面上的電流軌跡仍能大致保持橢圓軌跡，而id2-id3差分平面上的電流軌跡受噪聲干擾嚴重，已無法分辨形狀。

圖3 噪聲下的差分平面軌跡

當互感器發生飽和時，將二次電流折算到一次側后，其波形及在差分平面上的軌跡如圖4所示。由圖4可知，電流互感器飽和條件下，i-id1差分平面上的點仍集中在一個橢圓形區域內，而id1-id2差分平面上則出現了偏離原橢圓軌跡較遠的點。圖5顯示了一個周期內二次電流的畸變情況及其在id1-id2差分平面上的軌跡。系統采樣率為4 kHz，故在一個周期內共有80個點。設飽和時刻對應id1-id2差分平面上電流軌跡的第n個點。圖(b)、圖(c)分別為本周期內二次電流在開始飽和之前以及開始飽和之后的差分平面軌跡。由圖5可知，在飽和起始時刻附近，二次電流在id1-id2差分平面上的軌跡將偏離原橢圓形軌跡。

圖4 互感器飽和下的差分平面軌跡

圖5 飽和電流在id1-id2差分平面上的軌跡

由于飽和發生時二次電流在id1-id2差分平面上所對應的點將發生明顯的偏移，故可以使用id1-id2差分平面上連續兩點之間的距離來指示互感器的飽和情況。現定義變量dist來表征id1-id2差分平面上連續兩點之間的距離，dist可通過式(5)計算:

(5)

互感器在發生飽和及理想狀況下的dist值如圖6所示。由圖6可知若互感器不發生飽和，其dist波形接近于含直流偏置的正弦波。當互感器發生飽和時，在互感器飽和起始時刻，變量dist出現了明顯的極大值點。故可以通過設定閾值的方法來指示電流互感器的飽和起始時刻。此時互感器的飽和判據為：dist>th，其中th為閾值。

圖6 飽和及理想情況下的dist波形

2 互感器飽和補償

在檢測到電流互感器飽和起始時刻后，即可以判定電流互感器未發生飽和的區間。利用電流互感器未發生飽和的數據可對故障電流進行曲線擬合，從而實現對互感器飽和電流的補償。

最小二乘法是互感器飽和補償中常用的曲線擬合方法。然而若直接使用最小二乘法對二次電流進行曲線擬合，則需使用泰勒公式對直流衰減分量進行截斷處理，從而引入截斷誤差。故對原有最小二乘法進行改進，先求取直流衰減分量，再使用最小二乘法擬合穩態分量。

故障電流模型如式(4)所示，包含4個未知參數，故可使用4個未飽和的數據點求解。連續4個采樣點可如下表示：

(6)

式中T為采樣周期；ω為電網工頻的角頻率。通過三角變換由式(6)可得：

(7)

由此直流分量idc可如下計算：

(8)

計算衰減直流分量時，可在未飽和區間使用長度為4的滑動窗口計算不同時刻的e-T/τ值，并取其均值。為進一步提高計算精度，只選用未飽和區間中間部分的數據進行計算。若發現有大于等于1或小于等于0的e-T/τ，則舍去該值。Ie-kT/τ表征時間窗內k時刻直流分量的大小，故可以利用式(8)將不同時間窗計算得到的Ie-kT/τ折算到的同一時刻，再取平均。

計算得到直流衰減分量后，將其與原信號做差即可得到穩態正弦分量。穩態正弦分量iac可通過最小二乘法擬合：

iacn=IfcosωnT+θ

=IfcosωnT)cos(θ-IfsinωnTsinθ

(9)

設Ifcos(θ)、-Ifsin(θ)為系數a1、a2，cos(ωnT)、sin(ωnT)為變量x1、x2，則由最小二乘擬合可得：

(10)

因此最終互感器二次電流的擬合公式為：

(11)

3 飽和檢測算法

將差分平面法與改進最小二乘法相結合可實現電流互感器飽和的準確檢測與有效補償。差分平面法可用于檢測電流互感器的飽和起始時刻。當dist值大于閾值時即判定為飽和起始時刻。不飽和情況下的dist值由采樣頻率和穩態故障電流幅值決定。因此故障發生后，不飽和情況下各周期內dist的最大值保持不變。文獻[12]指出電流互感器飽和通常不會在故障發生后的前六分之一個周期內出現。采樣頻率為4 kHz時，可用采樣得到的前13個點確定閾值，閾值可設為：

th=M+4S

(12)

式中M為故障開始后前13點dist數據的均值;S為前13點dist數據的標準差。

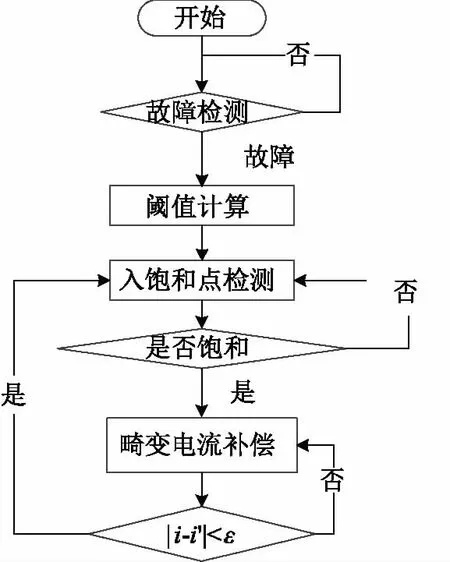
圖7 基于差分平面法的CT飽和檢測流程

4 仿真實驗

通過PSCAD/EMTDC對雙機系統進行仿真，從而檢驗文中算法的性能，仿真系統模型如圖8所示。其中互感器采用JA模型，其互感器沒有剩磁，磁路長度為0.637 7 m，鐵芯截面積為2.601e-3 m2，負載電阻為0.5 Ω，負載電感為0.8e-3 H。飽和檢測時，二次電流測量值均折算到一次側。

圖8 實驗系統模型

系統在0.02 s時發生短路故障，故障后前0.08 s內互感器電流波形及使用三階差分法、差分平面法檢測電流互感器飽和時刻的結果如圖9所示。圖9中圖(a)的藍線與綠線分別為飽和電流波形和理想電流波形。圖(b)為二次電流三階差分。圖(c)為二次電流的dist值。由圖9可知，在故障發生后的前幾個周期里，互感器飽和嚴重。此時互感器二次電流的三階差分、dist值均能良好的指示互感器的飽和起始時刻。

系統故障后的第4個周期至第8周期的飽和電流波形及其三階差分、dist值如圖10所示。由圖10可知，由于故障電流直流分量的衰減，此時互感器飽和程度較為微弱。對比圖10的圖(b)和圖(c)可知，在互感器微弱飽和的情況下，dist值比三階差分有更強的互感器飽和檢測能力。

圖9 故障發生前期

圖10 故障發生后期

系統故障后使用差分平面法的飽和起始時刻檢測結果如表1所示。由表1可知，差分平面法可以準確測量互感器的飽和起始時刻，本算例中其最大誤差為0.25 ms。

表1 飽和時刻檢測結果

使用文中的最小二乘法對互感器飽和畸變電流進行補償，其補償結果及補償相對誤差如圖11所示。

圖11 改進最小二乘法飽和電流補償結果

其中補償相對誤差定義為：

(13)

圖12 最小二乘法飽和電流補償結果

飽和結束時刻真實時間/ms檢測結果 /ms誤差/ms飽和結束時刻138.538.75-0.25飽和結束時刻257.25570.25飽和結束時刻376.7576.250.5飽和結束時刻496.2595.750.5飽和結束時刻5116115.750.25飽和結束時刻6136135.50.5飽和結束時刻7155.75155.50.25飽和結束時刻8175.75175.50.25

5 結束語

針對互感器飽和后將影響電流測量精度、導致保護誤動的問題，提出了一種電流互感器飽和檢測、補償的新方法。使用互感器二次電流的一階差分作為橫坐標、二階差分作為縱坐標組成差分平面，利用差分平面上連續各點之間的距離來檢測互感器飽和。在判斷得到電流互感器飽和起始時刻后，使用改進的最小二乘法對飽和電流進行校正。PSCAD仿真證明：(1)文中方法可實現電流互感器飽和的準確檢測與有效補償；(2)基于差分平面的電流互感器飽和檢測方法相對傳統的差分方法有更強的飽和檢測能力；(3)文中補償方法相對直接使用最小二乘法進行補償有更高的精度；(4)文中方法適用于不同工況下的電流互感器飽和檢測、補償，且無需互感器的相關參數。