FSAE賽車轉向數據采集系統設計

黃 成，周岳斌，宋學前

（湖北文理學院機械工程學院，湖北 襄陽441053）

中國大學生方程式汽車大賽（FSAE）是一項由高等院校汽車工程或汽車相關專業在校學生組隊參加的汽車設計與制造比賽。各參賽車隊按照賽事規則和賽車制造標準，自行設計和制造出一輛在加速、制動、操控性等方面具有優異表現的小型單人座休閑賽車，能夠成功完成全部或部分賽事環節的比賽。FSAE賽車轉向數據采集系統用于對轉向機構的監測，只需讀取競賽時的轉向角位移的數據，就可以實現對轉向的實時監控和數據記錄[1]。實時反饋回的轉向角位移數據反映了賽車工況，通過數據分析，就可以進一步改進賽車轉向設計的缺陷。因此，轉向數據采集系統的設計對于賽車轉向的調校和賽車手的訓練來說尤其重要。

1 系統架構

轉向數據采集系統的總體架構如圖1所示，處理器選用STM32F103系列芯片，具有64KB SRAM、512KB FLASH、1個 SDIO接口以及 3路 12位的ADC和112個通用的I/O等[2]。該數據采集系統中，用3路ADC分別采集轉向機齒輪的轉角、內轉向輪轉角、外轉向輪轉角，同時讀取三個角位移的模擬量大小，通過MCU將模擬量轉換成數字量，從而獲取某時刻賽車內外轉向輪以及轉向機齒輪角位移大小，并將處理后的數據通過無線通信模塊傳回到PC，然后采用MATLAB進行建模和軟件分析，具體控制流程如圖2所示。

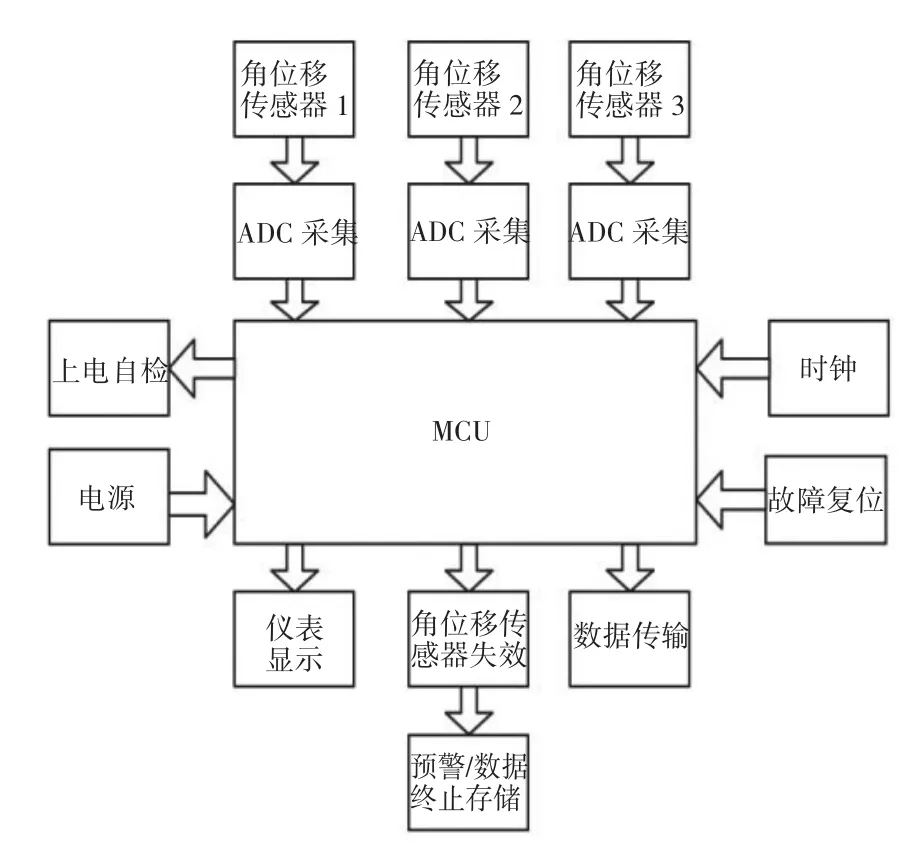
圖1 系統總體架構

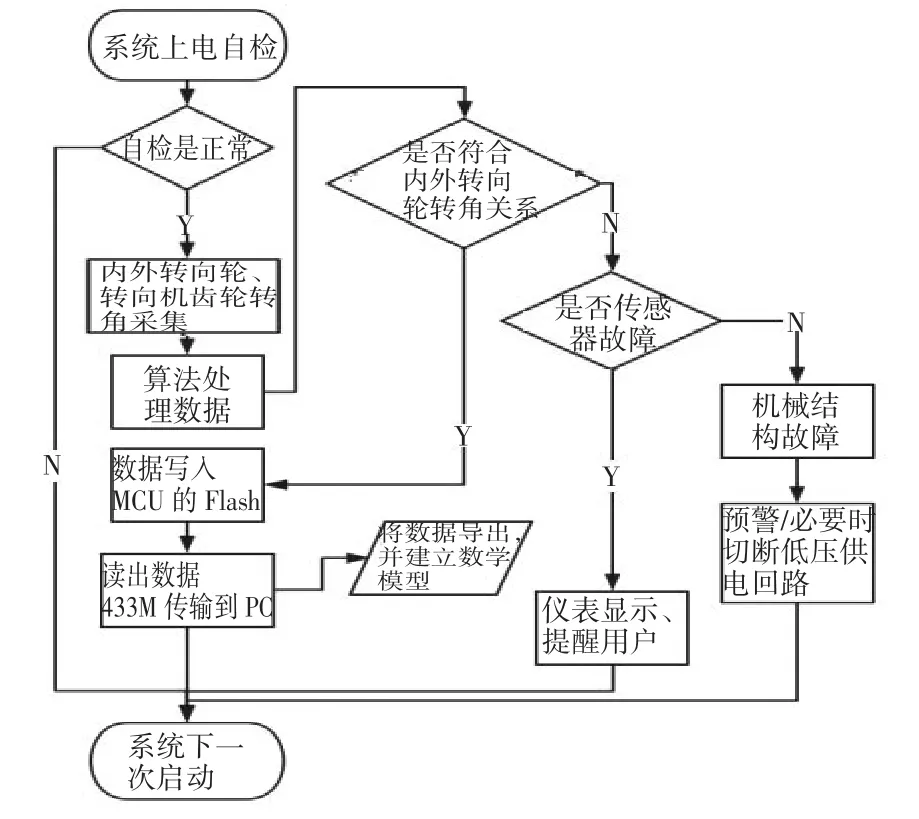
圖2 系統控制流程圖

考慮到角位移傳感器和轉向機械零部件都有一定的壽命范圍，賽車在不同工況下行駛時，可能會出現不同形式的失效，導致傳回數據異常，因此定義了兩種主要失效形式：傳感器失效、轉向機械結構失效。

2 角位移檢測與計算

角位移傳感器選用WDD35D4-1K角位移傳感器，傳感器模型如圖3所示，表1為其主要參數。

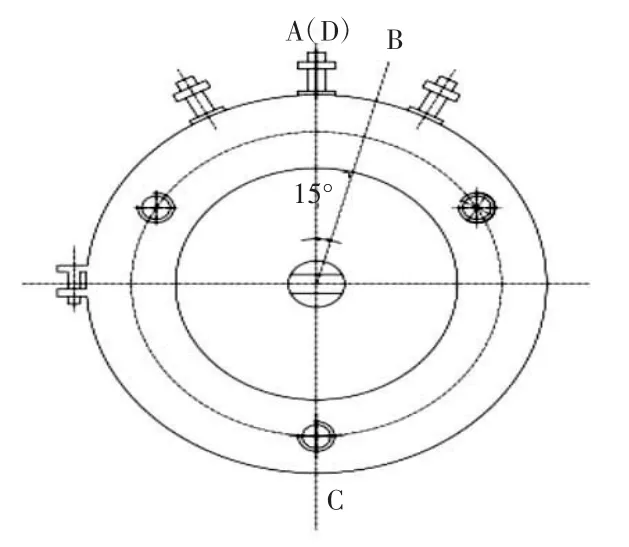
圖3 傳感器模型圖

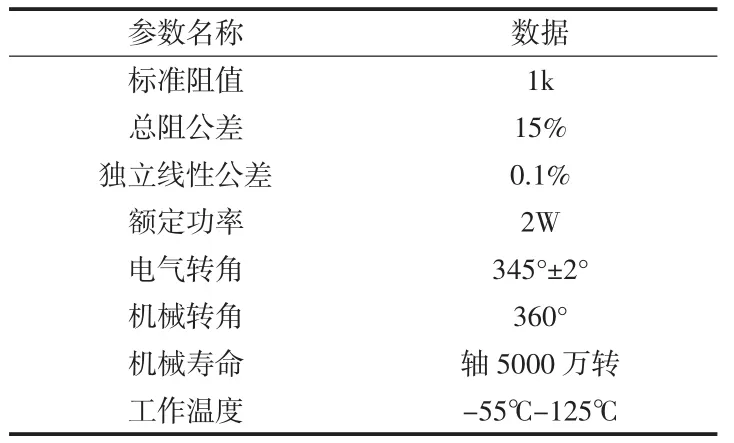
表1 傳感器參數表

考慮到方程式賽車的低壓電氣系統大多是5 V供電，傳感器也選用5 V供電，而MCU的ADC口一般只能承受3.3 V輸入電壓，因此加入一個運放跟隨電路，如圖4所示。運放跟隨輸入端進行RC濾波，輸出端采用精度0.01%、低溫漂的采樣電阻分壓，以保證電壓采集的精度和輸入到ADC口的最大電壓不超過3.3 V.

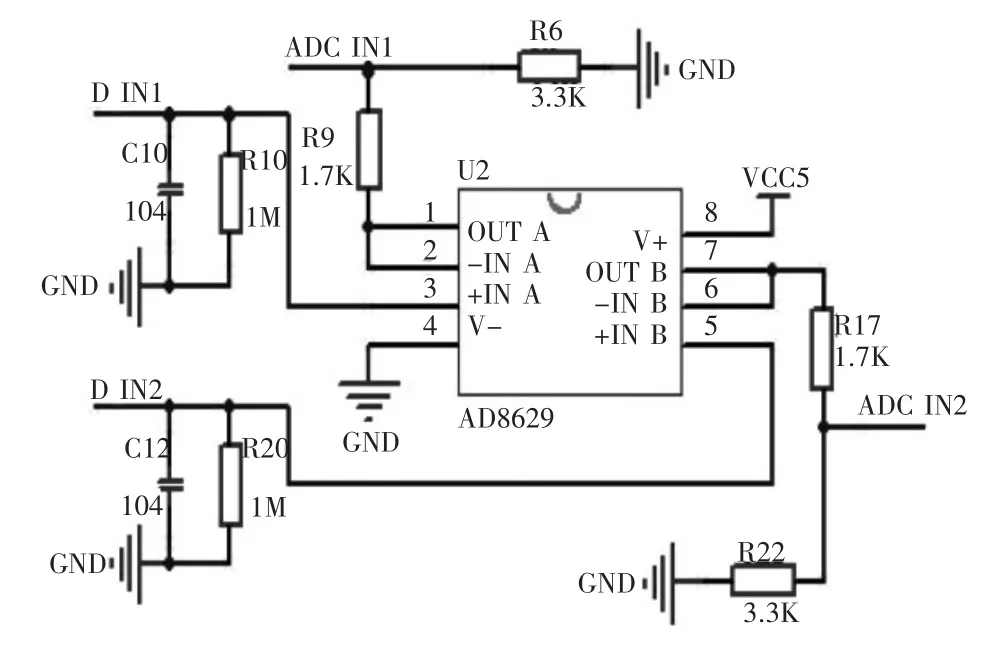
圖4 運放電路

根據表1可知角位移傳感器的電氣轉角與機械轉角在AB段不是一一對應的（電氣轉角最大為345°±2°，而機械轉角 360°連續），圖 3 中 A、B、C、D 分別代表機械轉角的 360°、345°、180°、0°，對應的電氣轉角分別為 0°、345°、180°、0°. 以傳感器轉軸 180°的位置為基準來安裝定位，當傳感器轉軸轉動方向：C點B點時，采集的電壓模擬量相對于基準位置是線性增加的；C點D點時，采集的電壓模擬量相對于基準位置又是線性減少的，從而可判斷某時刻賽車轉向的方向，也解決了機械轉角和電氣轉角AB段不對應對數據采集的影響。

MCU的ADC是12位模數轉換器，共有18個通道，各通道A/D轉換可以單次、連續、掃描或間斷模式執行，其輸入時鐘由PCLK2時鐘除以預分頻因子產生，最大不能超過14 MHz[3]。ADCCLK=14 MHz時，采樣周期為1.5個ADC時鐘，最小轉換時間為1 us.如果ADC的時鐘頻率超過14 MHz，會導致結果的準確度減小。對于每個要轉換的通道，采樣時間在保證轉換速率的前提下，盡可能選擇稍長的采樣時間，以獲得較高的準確度。

ADC的轉換時間的計算公式為：

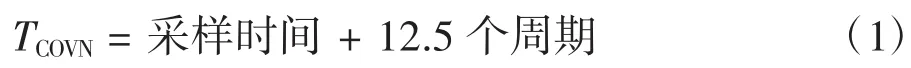
TCOVN為總轉換時間，采樣時間是根據每個通道SMP位的設置決定的[4]。在保證轉換速率的前提下，盡量提高數據準確度，選用采樣時間為239.5周期，設置時鐘分頻因子為6，則時鐘頻率為12 MHz（小于14 MHz），TCOVN=239.5+12.5=252 個周期 =21 us.為了滿足數據采集的同時性，ADC設置為三個不同通道進行采集，轉換模式為單次轉換。

C處參考電位為：

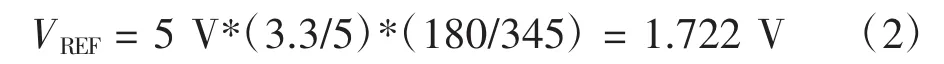
VB=5 V，VA=VD=0 V，因此任意時刻相對于參考電位的電位差為：

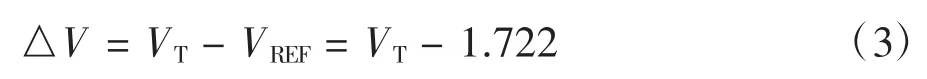
其中VT為任意時刻轉軸位置對應的電位，由公式（3）可以得出，任意時刻賽車轉向的方向及角位移大小，△V>0時，賽車的轉向方向向左，△V<0時，賽車的轉向方向向右。角位移大小為：

3 數據處理與分析

方程式賽車的轉向設計既要減少輪胎的磨損，延長輪胎使用壽命，也要具有良好的轉向操縱性和轉向穩定性。賽車大多采用斷開式轉向梯形結構，方向盤上的轉向力矩由轉向傳動機構傳到轉向機的齒輪上，再由齒輪帶動齒條移動。轉向橫拉桿兩端分別與轉向齒條和轉向節臂相連，在拉桿推力和拉力作用下轉向節臂帶動輪胎做轉動，從而實現轉向。合理的轉向梯形結構應使賽車轉向過程中四個轉向輪盡可能做純滾動，而不產生側滑，即四個轉向輪速度的瞬心交于同一點。當賽車后輪不發生轉向時，賽車的轉向中心應在后輪軸線上，此轉向關系即為理想阿克曼轉角關系，如圖5所示。

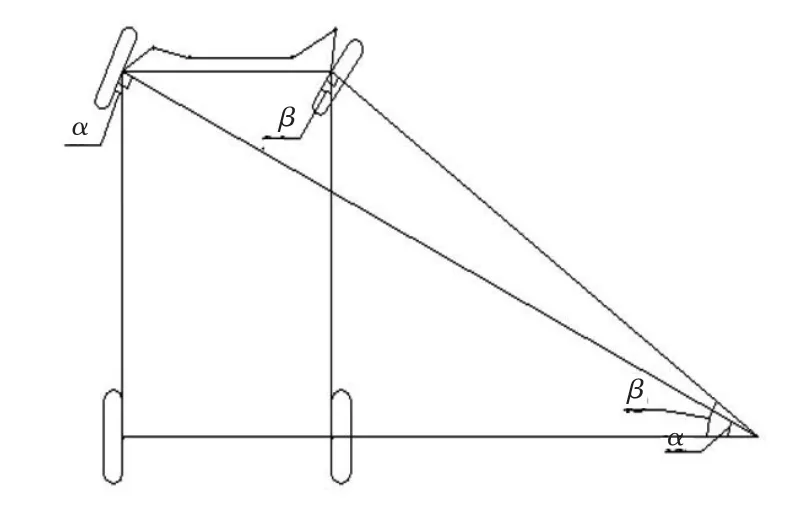
圖5 理想阿克曼轉角關系圖

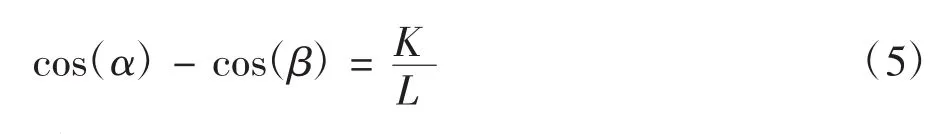
其中α為理想外轉向輪轉角，β為理想內轉向輪轉角，K為兩主銷中心距，L為輪距。

斷開式轉向梯形結構數學模型如圖6所示，依據此圖可計算相關轉向參數。

理想的內外轉向輪轉角關系為[5]：

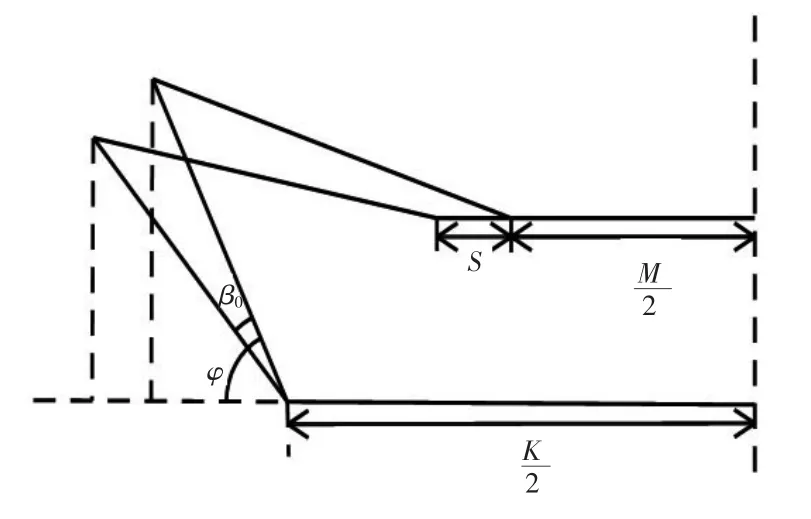
圖6 轉向梯形結構數學模型

內轉向輪轉角：

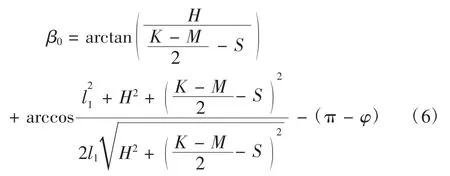
外轉向輪轉角：

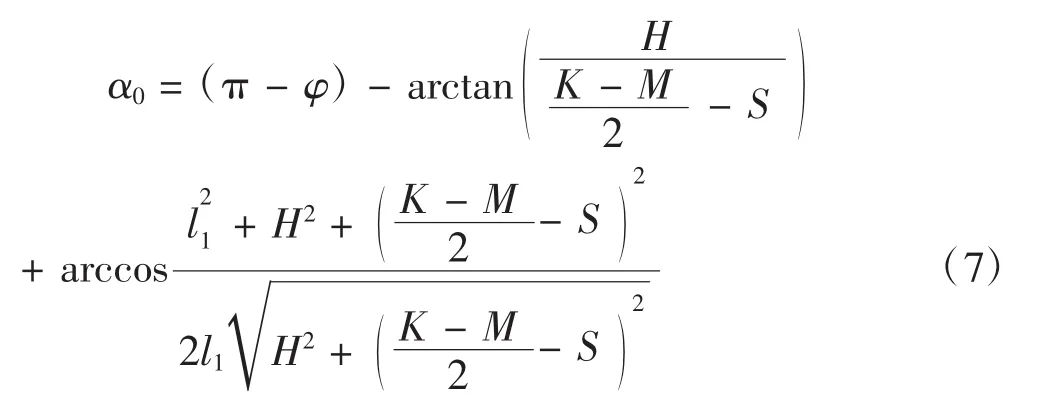
α0、β0為轉向模型設計得出的內外轉向輪轉角，而通過傳感器1、2獲取的是內外轉向輪的實際角位移量α1和β1，通過傳感器3獲取轉向機齒輪的角位移 Φ1，代入（8）式（W= Φ1）中求出 S，然后將 S代入式（5）可以求出α、β，然后用程序算法將每一次獲取的角位移量導入到阿克曼率公式中：

其中齒條單側行程由方向盤轉角大小決定，齒條單側行程與方向盤轉角的關系為：

計算出阿克曼率的值，每獲取5次ak，求一次平均值，以減少采集數據誤差。求出的阿克曼率，可矯正內外轉向輪轉角關系曲線，矯正后可以得到新的關系曲線。在實際轉向機構設計中，所設計機構的內外轉向輪轉角關系要與矯正后的關系曲線具有更高的擬合度，這樣可以使設計的轉向機構具有更好的操作性和穩定性，在比賽時才可以發揮出更優越的性能。

4 數據傳輸與故障處理

數據傳輸模塊選用433 M的無線傳輸模塊，具有以下特點：433 M為ISM頻段，靈敏度高，透明傳輸且傳輸距離遠，功耗低，抗干擾能力強，并且在傳輸速度和繞射性能上相對比較均衡。比賽賽場上，要求數據實時傳回，并且傳輸的抗干擾性能好，不受距離的影響，采用433 M無線傳輸，可以有效解決賽場上各種信號的對數據傳輸的干擾問題，確保了數據的實時性和準確性。MCU將處理后的數據發送到串口，利用無線傳輸模塊將數據傳回從機，并將數據通過串口打印出來，通過從機上的數據可以實時監控賽車的狀態，串口打印出的數據還可以保存成文本文件，導入MATLAB進行數學分析。見圖7、圖8.

圖7 采集系統實物圖

圖8 串口接收數據

考慮到競賽時，賽車在賽場上存在各種不確定因素，定義了兩種主要的故障：角位移傳感器故障、轉向機構故障，如表2所示。通過傳回到PC端的數據分析，若存在傳感器故障，此時定義故障等級為Ⅱ，儀表顯示轉向傳感器存在故障，及時將故障信息反饋給車手，提醒車手將賽車駛入指定的檢修區，進行故障排查及檢修；若存在轉向機構故障，此時定義故障等級為Ⅰ，儀表顯示轉向機構故障，提醒車手駛入避讓區，然后由車手拍下急停按鈕，切斷低壓回路，在避讓區等待相關技術人員的檢修[6]。必要時，由該采集系統的控制低壓回路的裝置，故障發生后主動切斷低壓回路，以防止車手未及時發現故障，避免出現安全事故。

表2 故障類型定義

5 結束語

轉向系統是用來改變或保持汽車行駛或倒退方向的一系列裝置，對汽車的行駛安全至關重要。本文提出了一種方程式賽車轉向數據采集系統的有效設計方案，可實現不同賽況下賽車轉向系統的實時監控，同時可對采集的轉向角度數據進行數學分析，有利于后期轉向機械結構優化設計，對大學生方程式賽車轉向系統的設計和優化也有一定的指導意義和參考價值。