基于動態(tài)系數(shù)的三次指數(shù)平滑算法負載預(yù)測

,, ,

(1.湖北大學(xué) 計算機與信息工程學(xué)院，武漢 430062; 2.湖北大學(xué) 楚才學(xué)院，武漢 430062; 3.烽火通信科技股份有限公司 業(yè)務(wù)與終端產(chǎn)出線，武漢 430073)

0 引言

2006年亞馬孫推出了云計算平臺之后，云計算就如火如荼地發(fā)展著。國外的如微軟、oracle、IBM等公司，國內(nèi)的阿里、騰訊、新浪等，在云計算上都取得一定的研究成果。云計算的核心技術(shù)就是虛擬化技術(shù)，其特點就是把數(shù)據(jù)中心的物理服務(wù)器虛擬成一個龐大的資源池，供用戶使用。虛擬化技術(shù)讓數(shù)據(jù)中心具有可伸縮的特點，提高數(shù)據(jù)中心的資源利用率，對應(yīng)用隔離，提高數(shù)據(jù)中心災(zāi)難恢復(fù)能力，減少碳排放量等起到重要作用。但是如何高效地利用數(shù)據(jù)中心資源池里面的CPU、內(nèi)存、硬盤、帶寬資源，已經(jīng)成為很多互聯(lián)網(wǎng)企業(yè)所面臨的問題。但是目前數(shù)據(jù)中心存在很多宿主機資源使用率不高的情況，比如天貓雙十一負載達到頂峰時期，宿主機資源使用率高，其他時期基本上很多宿主機都處于比較空閑的狀態(tài)，大量的資源使用率不高的宿主機導(dǎo)致一些不必要的資源浪費。如何均衡數(shù)據(jù)中心虛擬機負載，現(xiàn)在已成為云計算當(dāng)前的一個重點研究方向。云平臺如何負載均衡很大程度上取決于虛擬機未來負載的情況，由于數(shù)據(jù)中心的用戶訪問量每時每刻都在發(fā)生變化，當(dāng)前的負載情況往往不能決定數(shù)據(jù)中心未來的負載均衡策略，因此既要保證用戶的云服務(wù)體驗，又要避免大量的資源浪費，云平臺的負載均衡策略往往起到重要作用，而虛擬機負載預(yù)測是云平臺負載均衡策略的重要依據(jù)，因此虛擬機在未來時期的負載預(yù)測[1]對整個云平臺負載均衡調(diào)控尤為重要。當(dāng)虛擬機的實際負載高于預(yù)測負載時，由于資源不足導(dǎo)致整個云平臺的響應(yīng)速度過慢，以至于影響用戶體驗。當(dāng)虛擬機的實際負載又遠遠小于預(yù)測負載，則會導(dǎo)致一部分物理服務(wù)器過多的資源處于空閑狀態(tài)。因此，數(shù)據(jù)中心的負載預(yù)測對減少整個數(shù)據(jù)中心資源的消耗以及提升云服務(wù)體驗都起到重要的作用。

基于這種情況，本文采用指數(shù)平滑法[2-5]預(yù)測數(shù)據(jù)中心的未來負載情況，該算法在時間序列預(yù)測模型中得到了大量的實驗證明，其預(yù)測結(jié)果有一定的說服力。然而該算法有一個缺點，其預(yù)測系數(shù)沒有一個明確的求解方法，一般是由人為經(jīng)驗估算得出，并且不能隨著實際情況動態(tài)地改變其預(yù)測系數(shù)，導(dǎo)致預(yù)測負載與真實情況存在較大的誤差。在這種背景下，本文設(shè)計了一種基于動態(tài)系數(shù)[6-8]的三次平滑指數(shù)來預(yù)測數(shù)據(jù)中心負載走向。

1 虛擬機負載預(yù)測

在云計算平臺中，隨著虛擬機的負載越來越大，就意味著對虛擬機對宿主機的資源使用率越來越高。如果宿主機的資源使用率(包括計算、I/O等)達到一定范圍，則會導(dǎo)致該宿主機上的虛擬機出現(xiàn)對資源競爭的情況，導(dǎo)致云服務(wù)的響應(yīng)速度變慢。為了避免這種情況的出現(xiàn)，VMM(虛擬機管理器)能夠及時調(diào)控能起到關(guān)鍵作用，因此虛擬機負載預(yù)測對整個云平臺的負載均衡調(diào)控十分重要。

1.1 時間序列預(yù)測算法

時間序列預(yù)測算法包含移動平均法[9]、指數(shù)平滑法、BP神經(jīng)網(wǎng)絡(luò)預(yù)測算法[10-11]、回歸預(yù)測法[12]等。移動平均法將近期和遠期數(shù)據(jù)進行平均化，因此只適合近期變化不大的時間序列進行預(yù)測。如果序列處于某種上升或者下降比較明顯的趨勢時，就不適合作為該序列的預(yù)測算法。指數(shù)平滑法根據(jù)上期的預(yù)測值與真實值，通過加權(quán)的方式預(yù)測下一期的走勢，其優(yōu)點就是不用保存大量歷史數(shù)據(jù)，節(jié)省很多內(nèi)存空間，是一種廣泛使用的預(yù)測算法。BP神經(jīng)網(wǎng)絡(luò)預(yù)測算法其基本原理是輸入信號Xi通過隱層點作用于輸出層點，經(jīng)過非線性轉(zhuǎn)換，產(chǎn)生輸出信號Yk。如果在輸出層得不到期望的輸出，則使誤差往梯度方向下降，經(jīng)過反復(fù)的學(xué)習(xí)訓(xùn)練，最終得到誤差最小的網(wǎng)絡(luò)系數(shù)。該算法優(yōu)點就是非線性序列預(yù)測精準(zhǔn)度高，具有自學(xué)習(xí)與自適應(yīng)能力，有一定的容錯能力，缺點就是其算法本質(zhì)上是梯度下降法，需要進行復(fù)雜的科學(xué)計算，導(dǎo)致其學(xué)習(xí)速度很慢。回歸預(yù)測法是在自變量與因變量相關(guān)關(guān)系基礎(chǔ)之上，建立變量之間的相關(guān)方程，并將方程作為預(yù)測模型。根據(jù)自變量個數(shù)的不同，分為一元回歸預(yù)測法和多元回歸預(yù)測法。該算法的優(yōu)點是在分析多因素模型中，更加簡單方便，缺點就是需要大量的歷史數(shù)據(jù)計算才能得到回歸因子。

1.2 指數(shù)平滑法

指數(shù)平滑法由布朗提出，它是一種特殊的加權(quán)移動平均法，通過加權(quán)平滑系數(shù)，在時間序列模型中通過上一期預(yù)測值與真實值加權(quán)平均得到下一期的預(yù)測值。其數(shù)學(xué)表達式為:

yt+1=yt+α(xt-yt)

(1)

式中，xt是上期的觀測值，yt是上期的預(yù)測值，yt+1是下階段的預(yù)測值，指數(shù)平滑算法只需要上期的預(yù)測值與觀測值，不需要大量的數(shù)據(jù)計算，減少對服務(wù)器的負載壓力。在指數(shù)平滑算法中，預(yù)測成功的關(guān)鍵是α的選擇。α的大小規(guī)定了在新預(yù)測值中新數(shù)據(jù)和原預(yù)測值的比例。α值越大，新數(shù)據(jù)所占的比例就越大，原數(shù)據(jù)所占比重就越小，反之亦然。

1.3 三次指數(shù)平滑法

根據(jù)平滑次數(shù)的不同，指數(shù)平滑法分為一次指數(shù)平滑法、二次指數(shù)平滑法、三次指數(shù)平滑法等[13]。二次指數(shù)平滑法是建立在一次指數(shù)平滑法基礎(chǔ)之上的，適合預(yù)測線性時間序列，所預(yù)測的效果也優(yōu)于一次指數(shù)平滑法。若時間序列的走向呈現(xiàn)出拋物線式曲線，則需要采用三次指數(shù)平滑法進行預(yù)測，三次指數(shù)平滑法是在二次指數(shù)平滑法基礎(chǔ)之上再進行一次平滑[14]。由于數(shù)據(jù)中心的虛擬機負載時間序列呈拋物線狀，所以采用三次指數(shù)平滑法更為合適。不同次數(shù)的指數(shù)平滑法適用于何種類型的序列如表1所示。

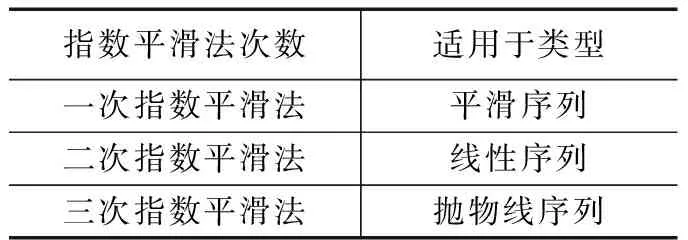
表1 不同平滑次數(shù)所適用序列

設(shè)數(shù)據(jù)中心虛擬機負載值為{Xt}(t=1,2,3…),第n時刻虛擬機負載一次、二次、三次指數(shù)平滑值分別記為St(1)、St(2)、St(3),各指數(shù)平滑值計算公式如下：

(2)

采用三次指數(shù)平滑法對t期后的q期數(shù)據(jù)進行預(yù)測得到，公式為：

Xt+q=at+btq+ctq2

(3)

其中:at、bt、ct為第t期的預(yù)測參數(shù)，計算公式為:

(4)

1.4 平滑系數(shù)的選擇

由于平滑系數(shù)的選擇對負載預(yù)測的影響很大，因此對于整體的預(yù)測模型十分重要。α取值范圍為0～1，一般情況下，根據(jù)經(jīng)驗，其取值范圍0.30～0.70[6]。α的取值一旦固定，則加權(quán)系數(shù)也隨之固定，即無法修改。由式(1)得知，在一次指數(shù)平滑預(yù)測模型中，α越大則歷史數(shù)據(jù)占的比例越高，α越小則預(yù)測數(shù)據(jù)占的比例就越高。因此α的取值大小，取決于模型對時間序列的變化速度，α取較小值時，預(yù)測序列平滑能力較強，反之模型對時間序列的變化反應(yīng)速度較快。當(dāng)時間序列呈現(xiàn)水平趨勢時，應(yīng)選取較小的序列值，常在0.10～0.30之間，序列有波動且長期趨勢變化不大時，可以選稍大的系數(shù)值，常在0.30～0.50之間取值，序列波動較大，呈現(xiàn)明顯上升或者下降時，可選擇較大的系數(shù)值，可以從0.60～0.80之間取值[15]。

“小荷才露尖尖角，早有蜻蜓立上頭。”盡管作者付出了諸多努力，也難以窮盡不斷涌現(xiàn)的新的理論和成果。愿這本《化學(xué)課程與教學(xué)論》能夠成為一股細微的源泉，溶入我國化學(xué)教學(xué)研究的潮流。

2 基于自適應(yīng)三次指數(shù)平滑系數(shù)負載預(yù)測

2.1 模型缺陷

傳統(tǒng)的指數(shù)平滑法能夠簡單高效地預(yù)測時間序列的走勢，但是模型有一個明顯缺陷，預(yù)測系數(shù)一旦確定就無法改變，無法根據(jù)時間序列的波動而動態(tài)變化。這種靜態(tài)的平滑系數(shù)導(dǎo)致預(yù)測過程中，無法適應(yīng)時間序列的動態(tài)變化的情況，對數(shù)據(jù)跳躍較為明顯的序列預(yù)測效果不佳。

在預(yù)測過程中，平滑系數(shù)反應(yīng)的是數(shù)據(jù)的變化趨勢。傳統(tǒng)模型中，平滑系數(shù)一旦確定即為一個常數(shù)，使得整個預(yù)測模型中自適應(yīng)能力低。在大多數(shù)應(yīng)用場景中，時間序列往往隨著時間的變化而發(fā)生動態(tài)變化，難以捕捉到其變化趨勢。本文所預(yù)測的數(shù)據(jù)中心負載波動往往較大，傳統(tǒng)的靜態(tài)三次指數(shù)平滑法無法適應(yīng)環(huán)境的變化，導(dǎo)致預(yù)測效果不佳。這也表明，動態(tài)系數(shù)在指數(shù)平滑預(yù)測模型中顯得越來越重要，能夠適應(yīng)過去數(shù)據(jù)變化的能力，采用動態(tài)系數(shù)對過去的系數(shù)進行一個修正，實驗表明動態(tài)系數(shù)在整個預(yù)測模型中起到?jīng)Q定性作用。

2.2 動態(tài)系數(shù)求取

在實際應(yīng)用中，為了讓三次指數(shù)平滑系數(shù)能更好的適應(yīng)環(huán)境的變化，達到更佳的負載預(yù)測效果，本文采用能夠動態(tài)變化的平滑系數(shù)。首先考慮到云平臺負載情況往往在某個時間段內(nèi)變化不大，根據(jù)負載變化將云平臺負載預(yù)測劃分為若干個時間段。對于不同時段，平滑系數(shù)α采用步長為0.01的迭代，通過反復(fù)訓(xùn)練α，提高預(yù)測的精準(zhǔn)度。具體步驟如下：

1)選定某個時段的歷史數(shù)據(jù)，采用等距法進行搜索最佳值。設(shè)定距長λ為0.01，則將α分為0.01相同的距離區(qū)間，記為αk(k=1,2…)。

2)根據(jù)誤差平方和最小原則選取最佳平滑系數(shù)，即在這個時間段選取誤差所對應(yīng)最小的平滑系數(shù)α。

(5)

3)通過步驟(2)得到最小誤差所對應(yīng)的系數(shù)α，新系數(shù)所預(yù)測的負載數(shù)據(jù)跟實際數(shù)據(jù)存在誤差，那么新的誤差值為之前誤差與新誤差二者的均值，并且覆蓋原來的誤差，即：

(6)

4)重復(fù)步驟2)、3)的操作，選取誤差所對應(yīng)最小的三次平滑系數(shù)，并將新預(yù)測的誤差與舊誤差二者的均值重新覆蓋原來的舊誤差。整個算法流程如圖1所示。

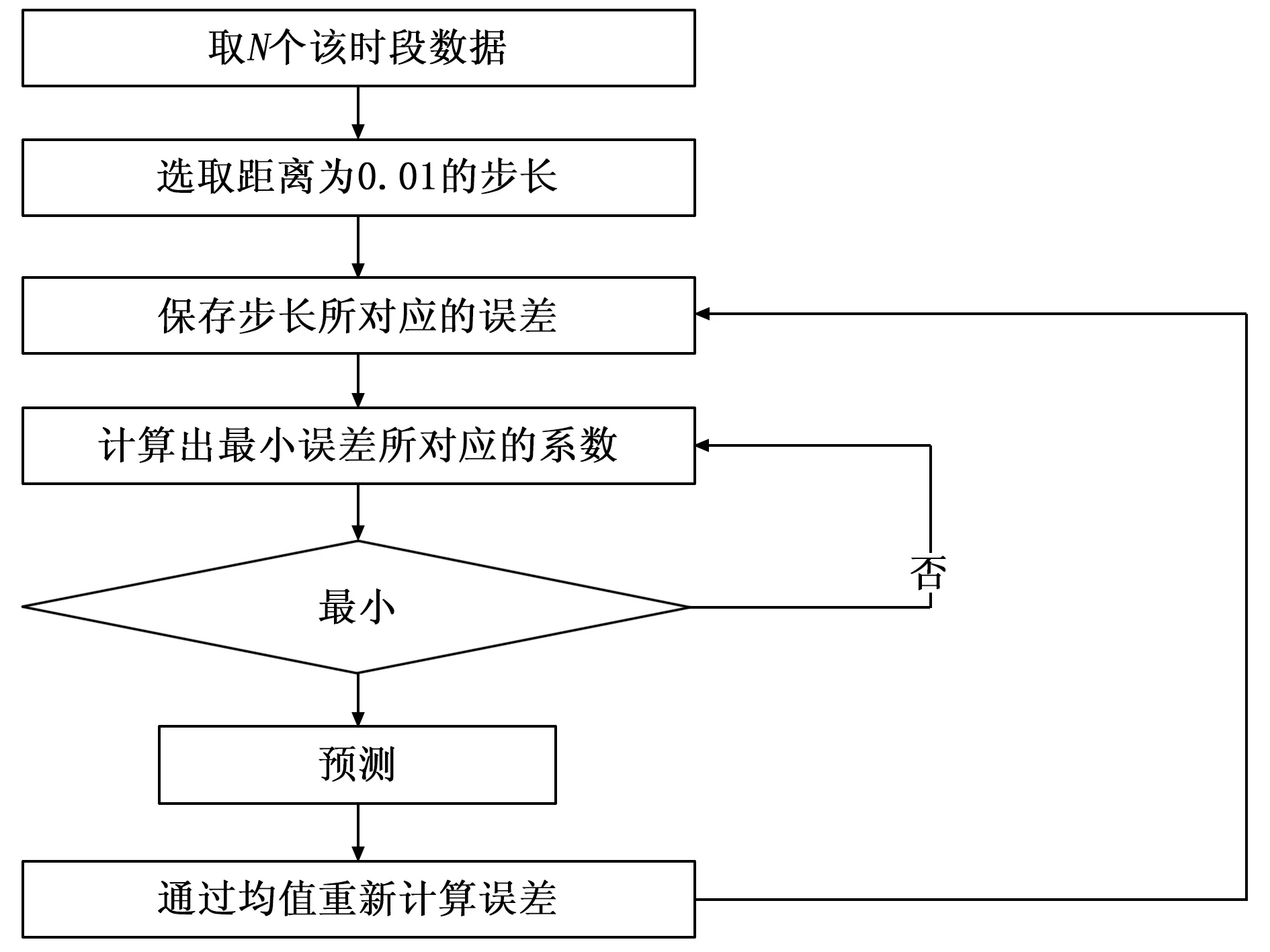
圖1 動態(tài)平滑系數(shù)求取流程圖

2.3 基于動態(tài)三次平滑系數(shù)負載預(yù)測

通過式(5)與式(6)得到最優(yōu)平滑系數(shù)，再通過式(2)～式(4)完成負載預(yù)測。本文采用誤差比對方式獲取最佳系數(shù)值，通過新一輪的預(yù)測再重新校對誤差，相比傳統(tǒng)的靜態(tài)系數(shù)預(yù)測更加精準(zhǔn)，此種方式不僅提高了預(yù)測的精準(zhǔn)度，同時也有效解決了負載暴增或者暴減的突發(fā)情況。

3 實驗及分析

為了驗證文中提出的基于動態(tài)系數(shù)的三次指數(shù)平滑算法預(yù)測的精準(zhǔn)度，本文采用某智慧農(nóng)業(yè)云平臺虛擬機負載時間序列作為本文的實驗數(shù)據(jù)。

3.1 驗證過程

假設(shè)在需要預(yù)測未來負載走向的數(shù)據(jù)中心上，其運行在物理服務(wù)器之上的虛擬機負載Li表示形式為：

Li=ui*pi

(7)

其中：ui表示虛擬機CPU的使用率，pi表示虛擬機CPU核心數(shù)量。若h0是一臺雙核心的虛擬云服務(wù)器，p0=2，現(xiàn)在CPU的使用率是0.3，那么L0=2*0.3=0.6。本文采用的智慧農(nóng)業(yè)云平臺某時期負載作為實驗數(shù)據(jù)對動態(tài)預(yù)測進行驗證,如表2所示。

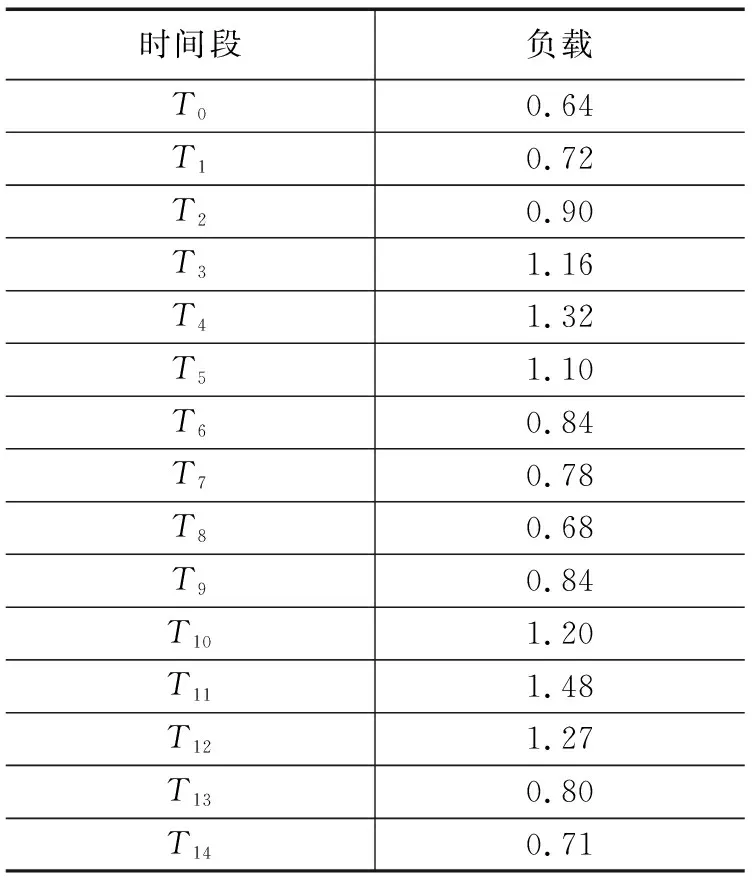
表2 智慧農(nóng)業(yè)云平臺某時期不同時段負載情況

通過對數(shù)據(jù)分析發(fā)現(xiàn)，智慧農(nóng)業(yè)云平臺虛擬機負載數(shù)據(jù)呈拋物線變化情況，可以用三次指數(shù)平滑算法進行預(yù)測。本文首先采用兩種靜態(tài)系數(shù)來預(yù)測，分別為0.30和0.50，用python語言繪制出初始值之后時段的預(yù)測值，對比兩種靜態(tài)系數(shù)所預(yù)測的效果，其結(jié)果如圖2所示。

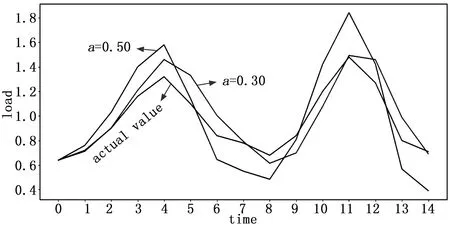
圖2 靜態(tài)系數(shù)與真實值對比結(jié)果圖

接下來采用動態(tài)系數(shù)進行預(yù)測，其預(yù)測結(jié)果與實際情況對比如圖3所示。

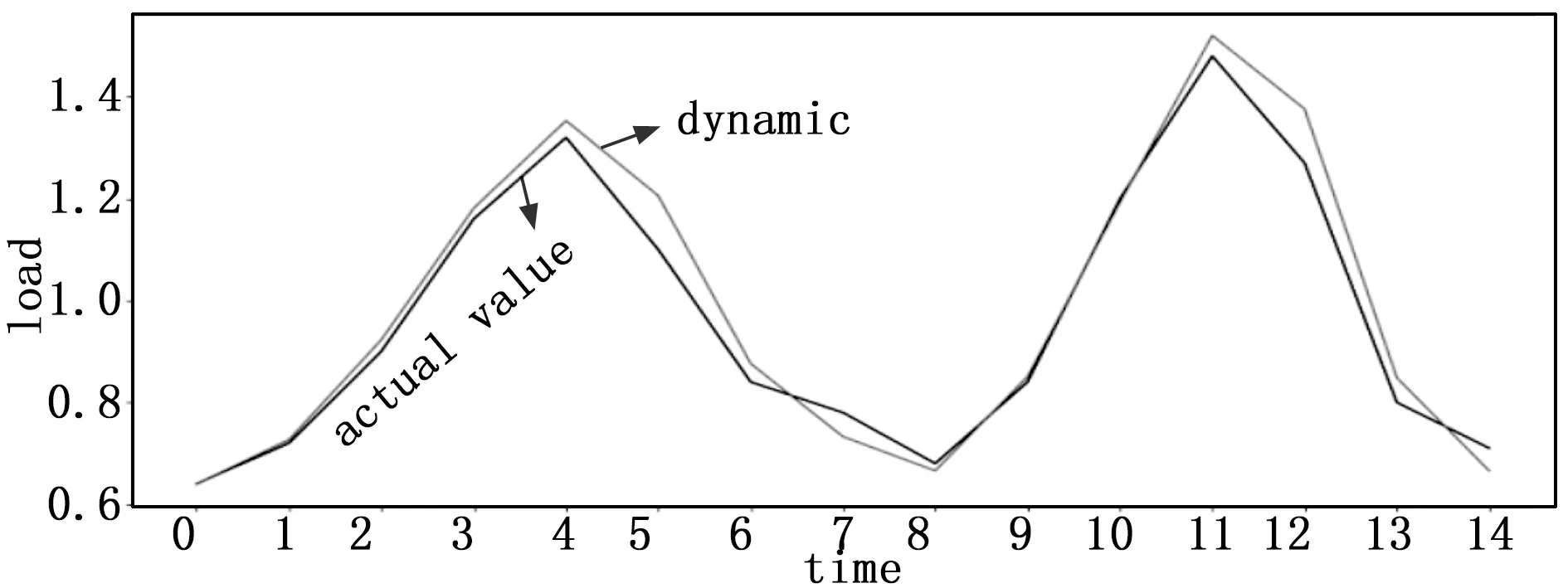
圖3 動態(tài)系數(shù)與真實值對比結(jié)果圖

3.2 結(jié)果分析

由圖2可知，靜態(tài)平滑系數(shù)為0.3所預(yù)測負載的準(zhǔn)確度比系數(shù)為0.5要高，更貼近真實值。而圖3所采用的動態(tài)系數(shù)是通過反復(fù)迭代尋找最小誤差所對應(yīng)的最優(yōu)解得到的，其預(yù)測負載準(zhǔn)確度較以上兩個靜態(tài)系數(shù)更高。實驗結(jié)果表

明，本文所采用的動態(tài)系數(shù)三次指數(shù)平滑法預(yù)測負載相比傳統(tǒng)的靜態(tài)系數(shù)準(zhǔn)確度更高，預(yù)測系數(shù)能夠隨著環(huán)境的變化而發(fā)生動態(tài)改變，計算復(fù)雜度低，在工程上具有一定的應(yīng)用價值。

4 結(jié)束語

本文采用基于動態(tài)系數(shù)三次指數(shù)平滑法預(yù)測數(shù)據(jù)中心虛擬機負載，傳統(tǒng)方法是采用靜態(tài)系數(shù)去預(yù)測未來的時間序列，其缺點是不能根據(jù)環(huán)境變化動態(tài)調(diào)整其預(yù)測系數(shù)。本文通過在不同時段采用等距迭代的方式反復(fù)測量不同系數(shù)的誤差情況來求解最佳系數(shù)，新系數(shù)預(yù)測出來的誤差又重新與舊誤差產(chǎn)生一個均值并覆蓋原來的誤差。實驗表明，本文提出的動態(tài)系數(shù)三次指數(shù)平滑法預(yù)測負載的誤差小于靜態(tài)系數(shù)，具有更好的實用性。