FIR數字濾波器零極點靈敏度分析及優化實現

莊陵，馬靖怡，王光宇，關鵑

?

FIR數字濾波器零極點靈敏度分析及優化實現

莊陵，馬靖怡，王光宇，關鵑

（重慶郵電大學移動通信技術重慶市重點實驗室，重慶 400065）

針對有限字長效應導致濾波器零極點的位置偏移問題，基于狀態空間實現結構研究FIR數字濾波器零極點對系數誤差的靈敏性。不同于IIR濾波器，FIR濾波器狀態空間模型中的系統矩陣具有虧損性。引入虧損矩陣廣義特征向量分析極點的靈敏性，導出靈敏度表達式，并依據相似變換理論找尋最佳變換矩陣，提出FIR濾波器零極點靈敏度的優化實現。理論推導及仿真實驗表明，FIR濾波器極點對系數誤差敏感度較高，且所提優化實現方案能夠降低靈敏度。

FIR數字濾波器；狀態空間實現；零極點靈敏度；虧損矩陣；廣義特征向量

1 引言

有限字長（FWL, finite word length）效應導致的系數量化會影響實際應用中濾波器的性能，使零極點位置發生偏移，從而改變頻率響應特性。研究系數變化的靈敏度有多種方式，一類基于衡量傳遞函數關于參數的擾動[1-3]，另一類基于測度系統零極點位置的偏差[4-5]。某些情況下相比于量化引起傳遞函數中的誤差，零極點位置偏移對濾波器性能產生的影響更為重要，例如，在設計陷波濾波器時需要保證零點位置的精確性，或對于閉環系統，其穩定性決定于極點（特別是主導極點）位置[6]。

值得注意的是，以上對零極點靈敏度的分析均基于IIR濾波器，而FIR濾波器相較于IIR濾波器有容易實現線性相位特性、適合多采樣率轉換等優點，廣泛應用于4G移動通信系統、視頻與圖像處理等領域。然而，FIR濾波器與極點靈敏度有關的系統矩陣為虧損矩陣，其特征向量系是線性相關的，不具有完備的特征子空間，因此，利用非虧損矩陣特征向量的獨立性分析極點靈敏度的方法已不再適用[14]。本文引入廣義模態理論，利用系統矩陣的一組滿足酉正交條件的廣義特征向量系及其伴隨向量系，對FIR濾波器的極點靈敏度進行理論推導及分析，同時給出FIR濾波器零極點靈敏度的優化方法。

2 FIR濾波器狀態空間實現背景理論

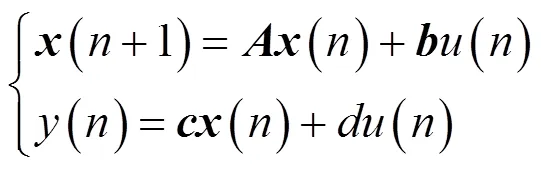
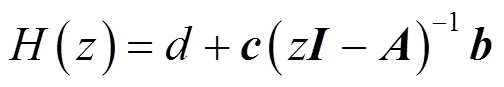
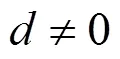
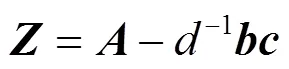
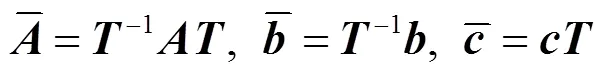
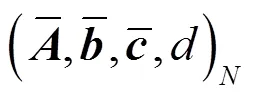
3 零點靈敏度及其最小化

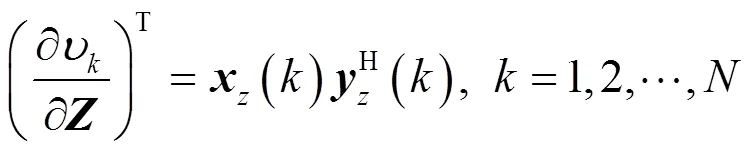
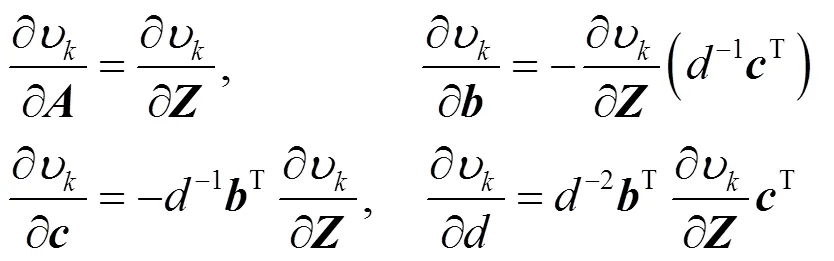
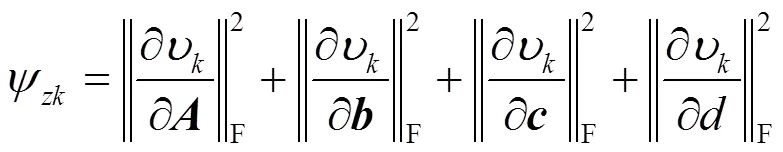
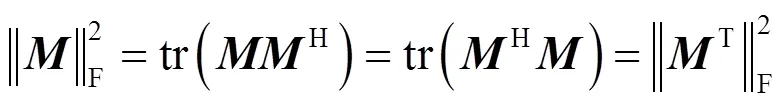
則式(7)亦可表示成

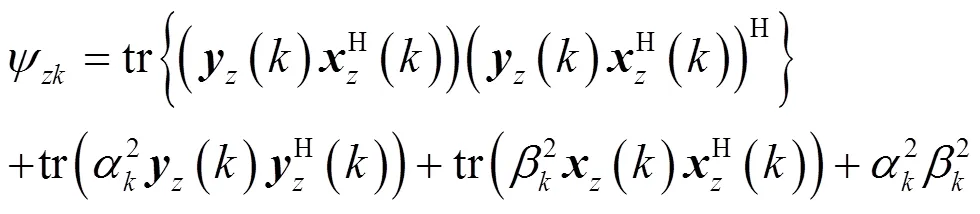
濾波器總的零點靈敏度為

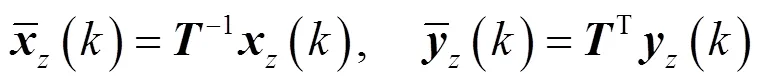
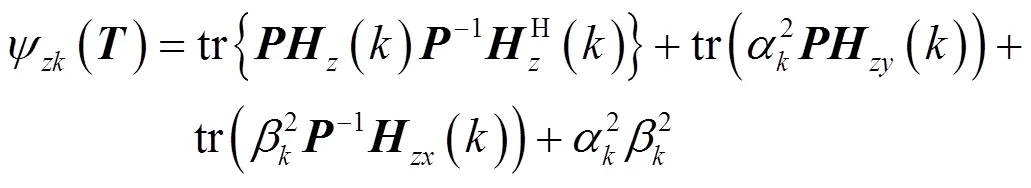
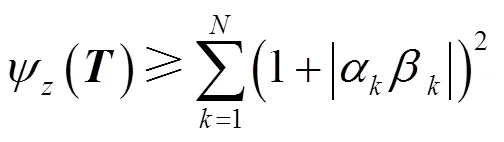
4 極點靈敏度及其優化

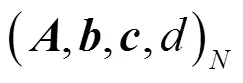
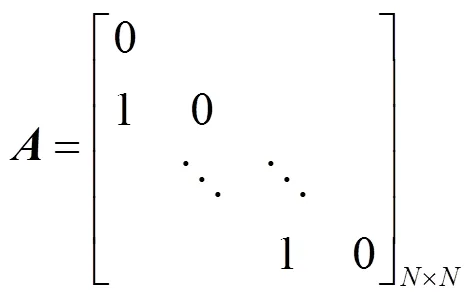
4.1 系統矩陣A的特征值擾動分析

系統矩陣是一個重虧損矩陣，由其結構可知存在如下形式的可逆矩陣

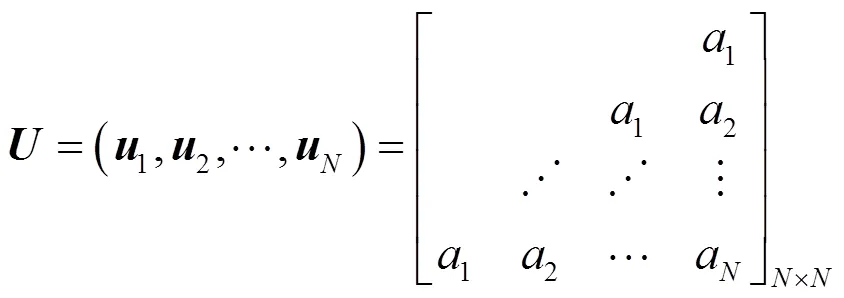
使

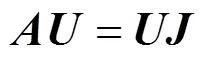
其中，是的Jordan標準型。下面對矩陣的列向量進行歸一化

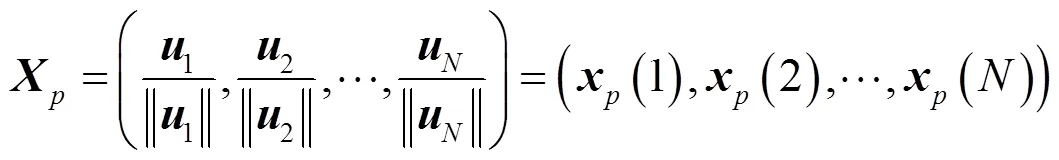
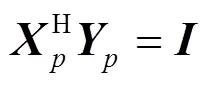
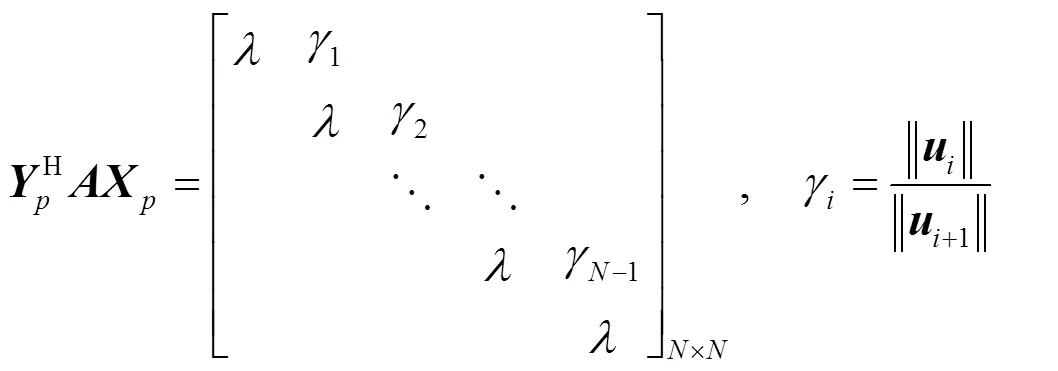
則矩陣受擾動后其特征值的表現形式如定理1所示。

定理1 若系統矩陣的元素產生擾動

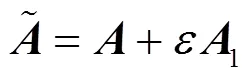
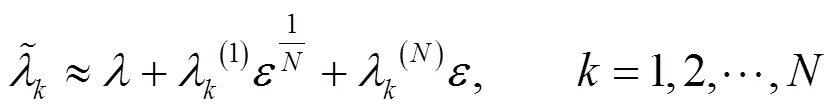
則有

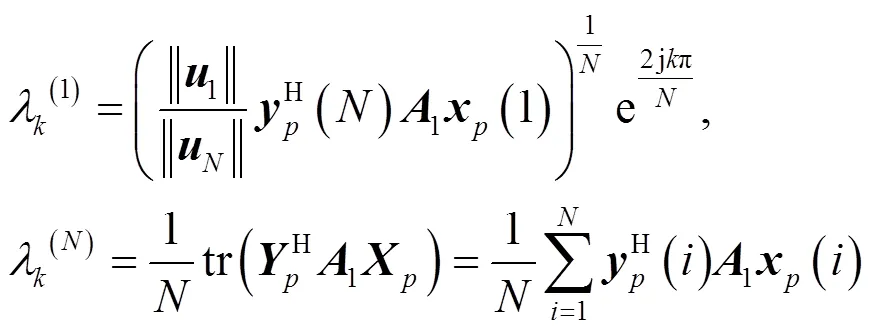
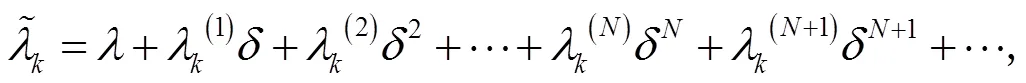
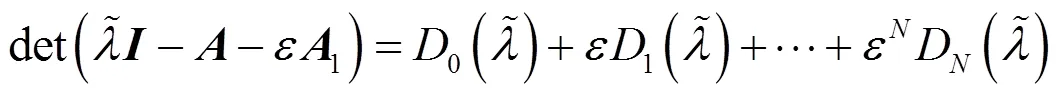
根據文獻[15]可推導出

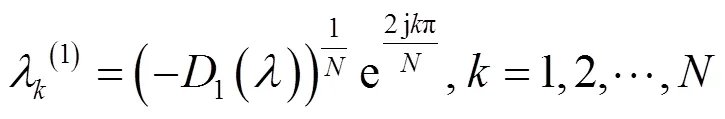
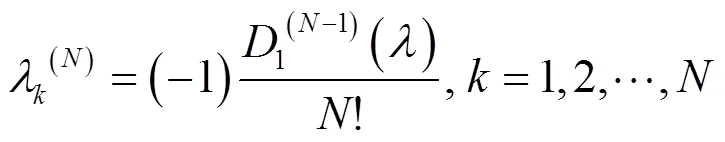
由特征值與矩陣跡和行列式關系的定義可得

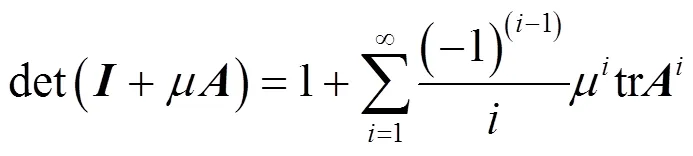
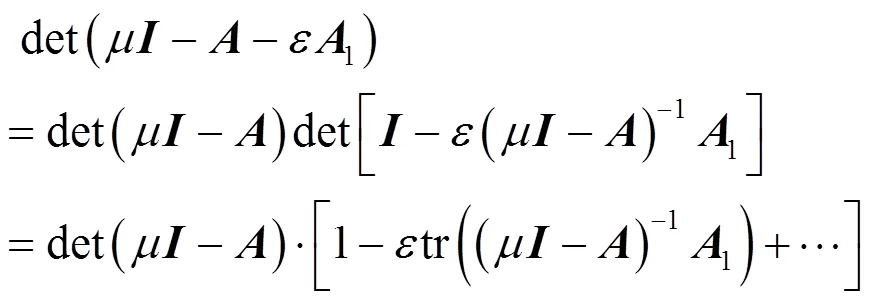
對比式(22)，可得

引入廣義特征向量矩陣

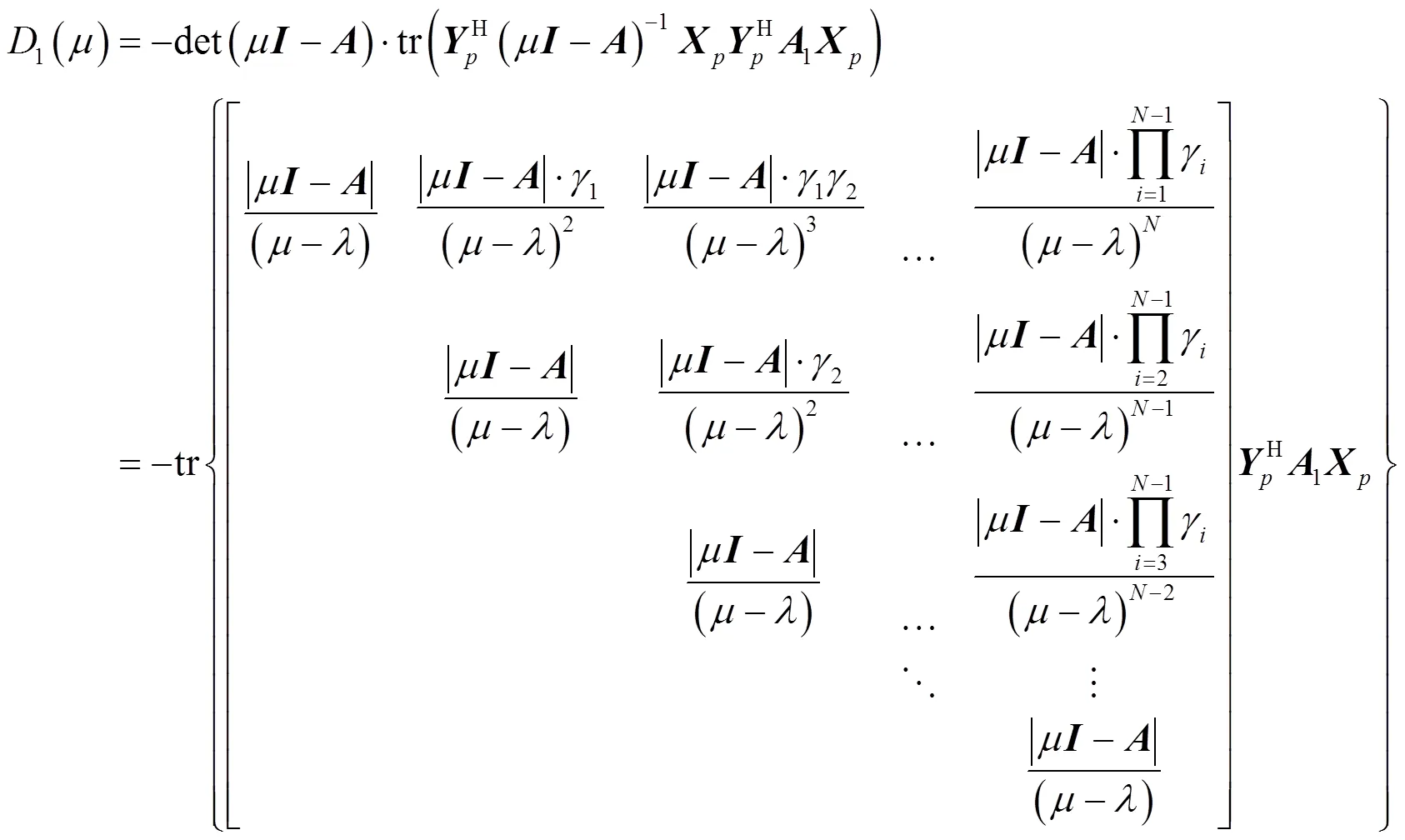
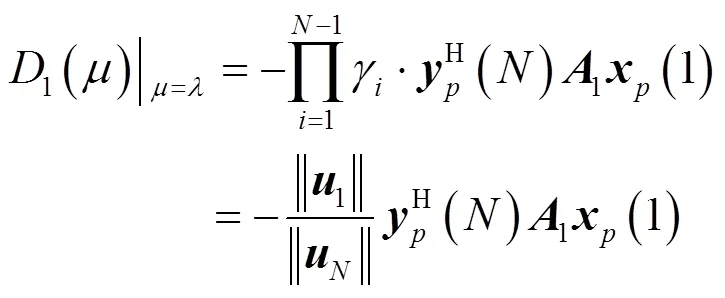
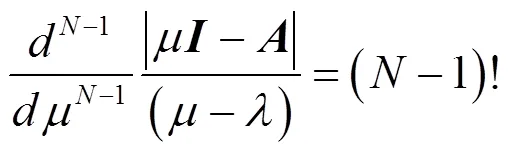
則有

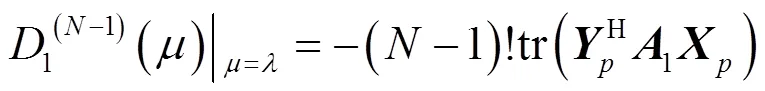
將式(29)和式(31)分別代入式(23)和式(24)，即可證得式(20)。

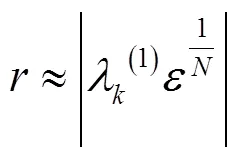
4.2 極點靈敏度優化

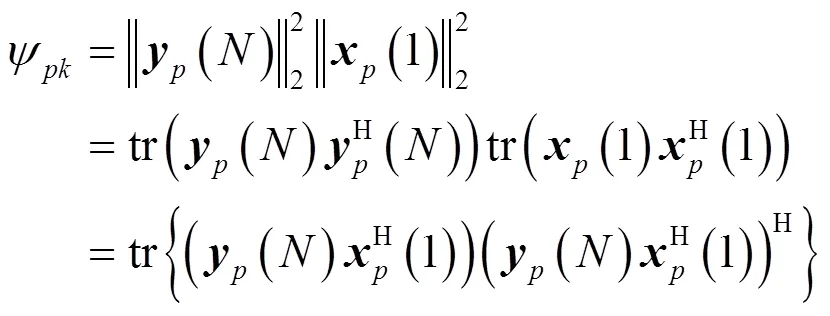
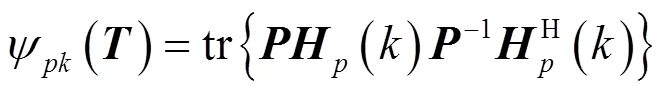
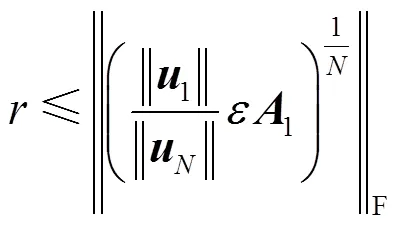
5 零極點靈敏度加權優化

在優化系統零極點靈敏度時，通常不能得到同時使兩者達到最優的狀態空間實現。最小化零點靈敏度可能優化不了極點靈敏度，甚至會惡化極點靈敏度。然而存在極點與零點擾動都會影響到系統性能的情況，或系統對某些極點（零點）上的擾動更為敏感。對零極點加上特定權重，可以權衡極點與零點靈敏度之間的優化。記系統的加權零極點靈敏度為

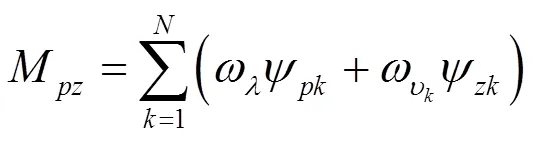
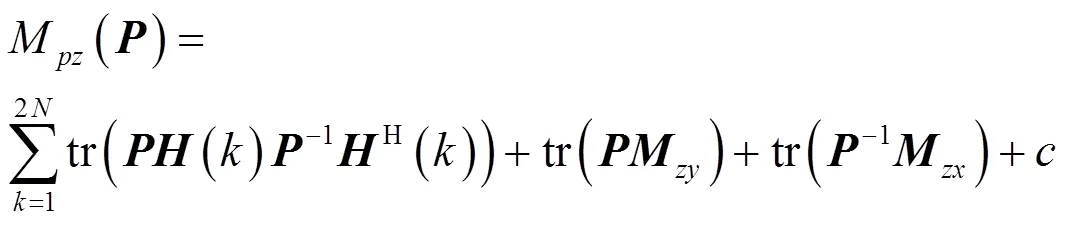
其中

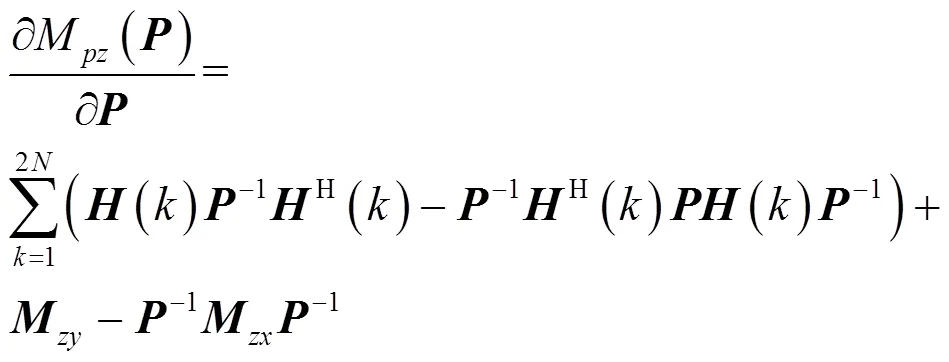
因式(38)等價于

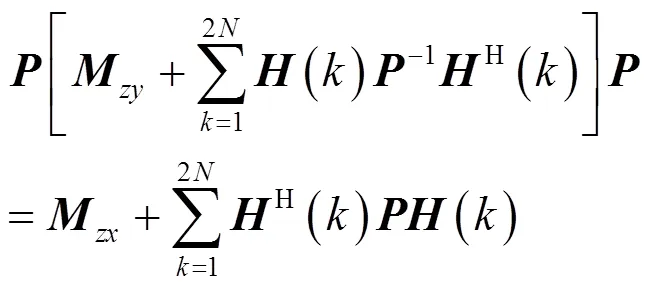
可令

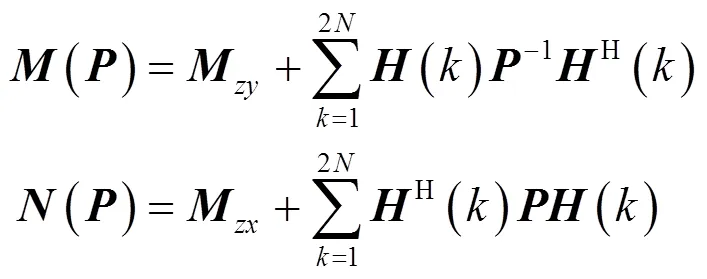
整理式(39)得

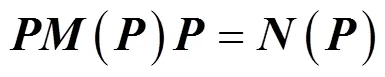
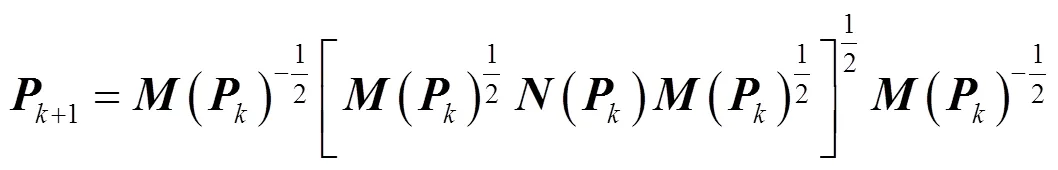
迭代終止條件

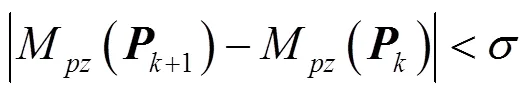
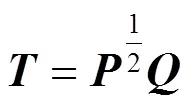
6 仿真實例

下面以23階線性相位FIR低通數字濾波器為例，利用matlab仿真平臺分析零極點的靈敏度以及零極點位置偏移對濾波器頻響特性的影響，并比較3種優化方案的優化性能。

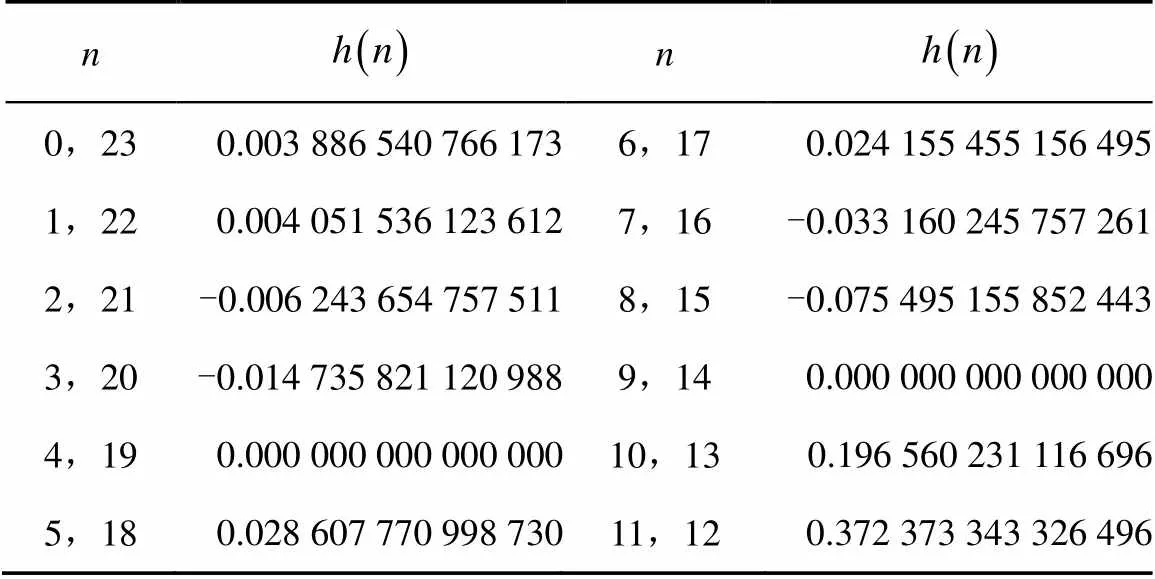
表1 23階線性相位下IR低通濾波器系數h(n)

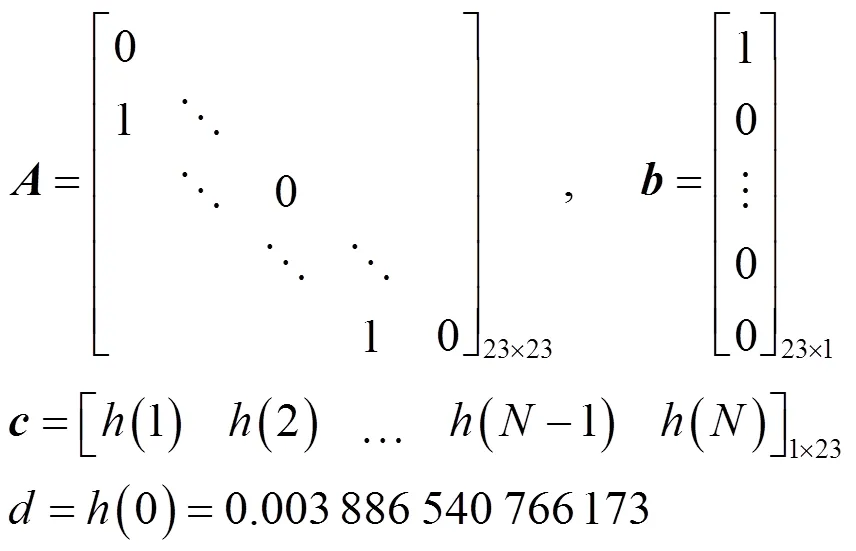
表2 不同實現的零極點靈敏度

6.1 系數擾動下的靈敏度分析

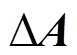
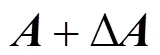
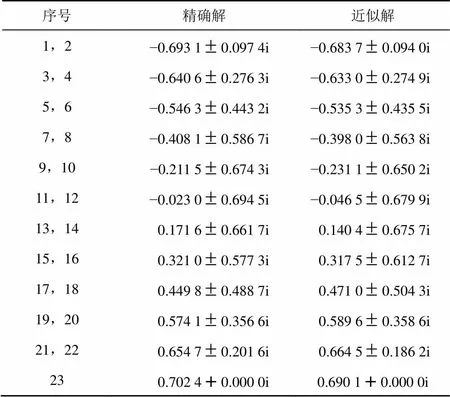
序號精確解近似解 1，2?0.693 10.097 4i?0.683 70.094 0i 3，4?0.640 60.276 3i?0.633 00.274 9i 5，6?0.546 30.443 2i?0.535 30.435 5i 7，8?0.408 10.586 7i?0.398 00.563 8i 9，10?0.211 50.674 3i?0.231 10.650 2i 11，12?0.023 00.694 5i?0.046 50.679 9i 13，140.171 60.661 7i0.140 40.675 7i 15，160.321 00.577 3i0.317 50.612 7i 17，180.449 80.488 7i0.471 00.504 3i 19，200.574 10.356 6i0.589 60.358 6i 21，220.654 70.201 6i0.664 50.186 2i 230.702 40.000 0i0.690 10.000 0i

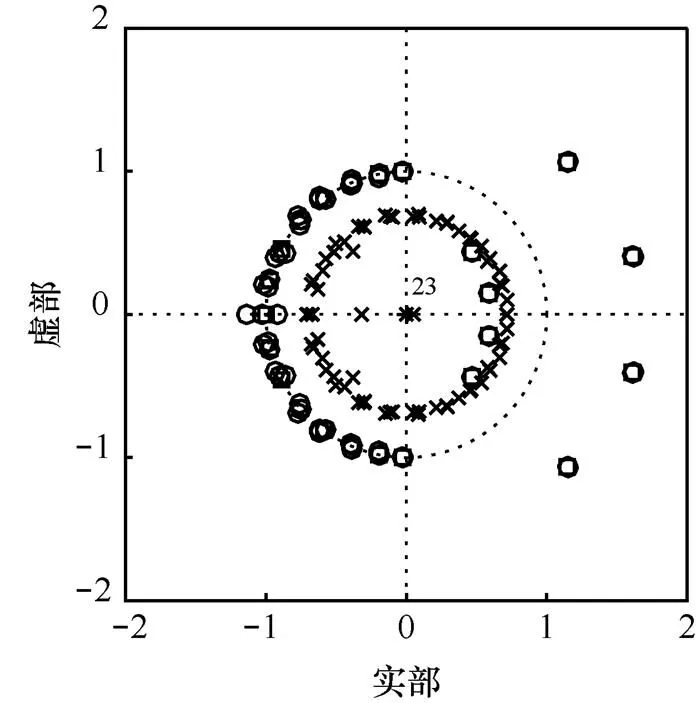
圖1 狀態空間實現下濾波器的零極點擾動分布

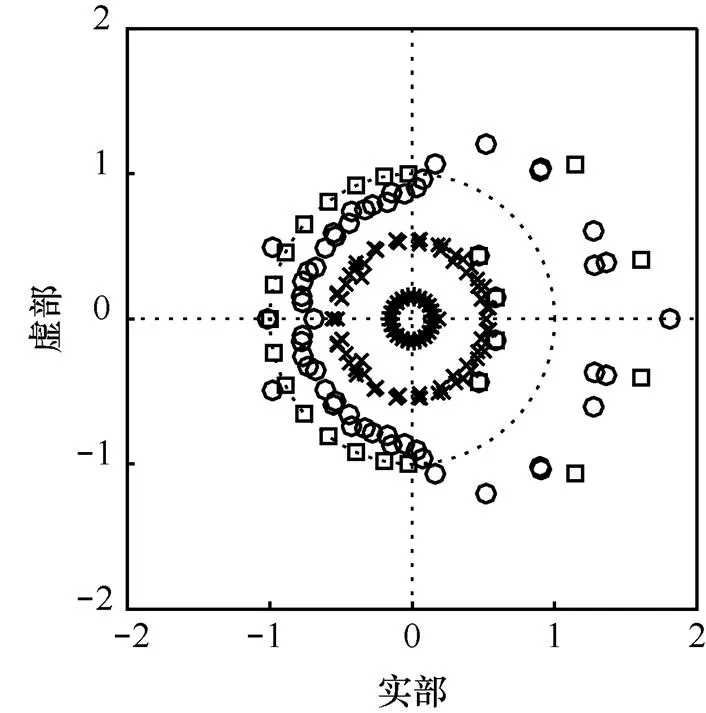
圖2 狀態空間實現下濾波器的零極點擾動分布

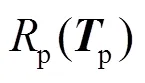
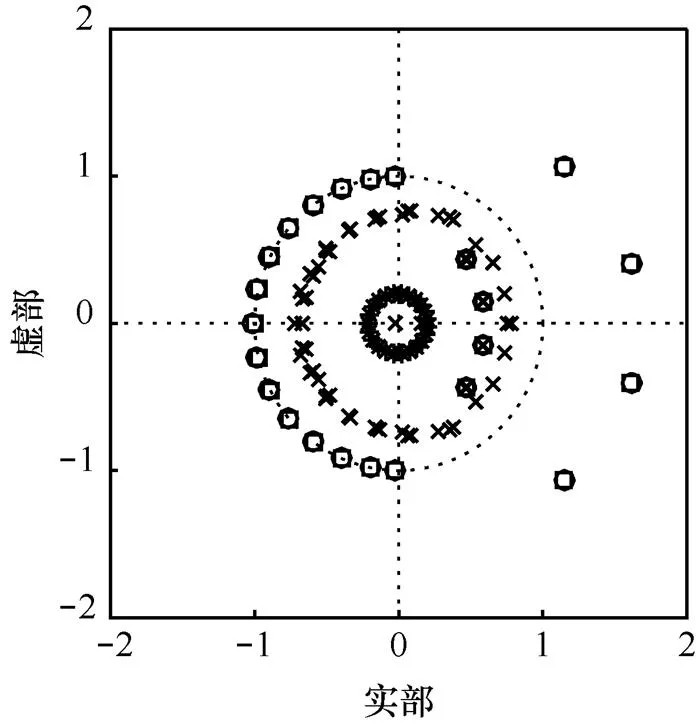
圖3 狀態空間實現下濾波器的零極點擾動分布

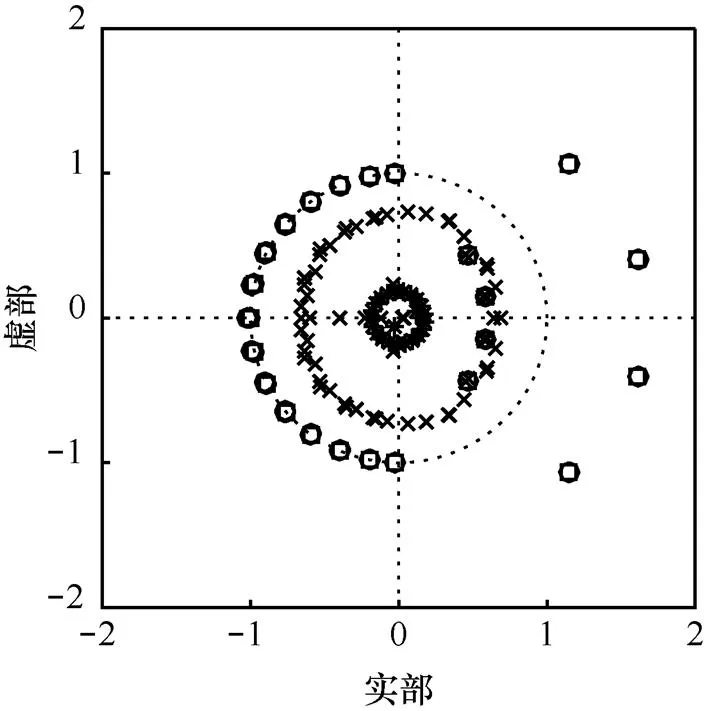
圖4 狀態空間實現下濾波器的零極點擾動分布

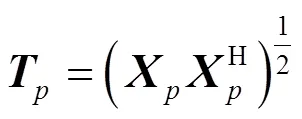
由于系統特性直接與系統函數零極點的分布有關，零極點位置偏移會改變系統原有的頻響特性。圖5~圖12分別對應圖1~圖4中擾動實現的幅頻響應與相頻響應變化。

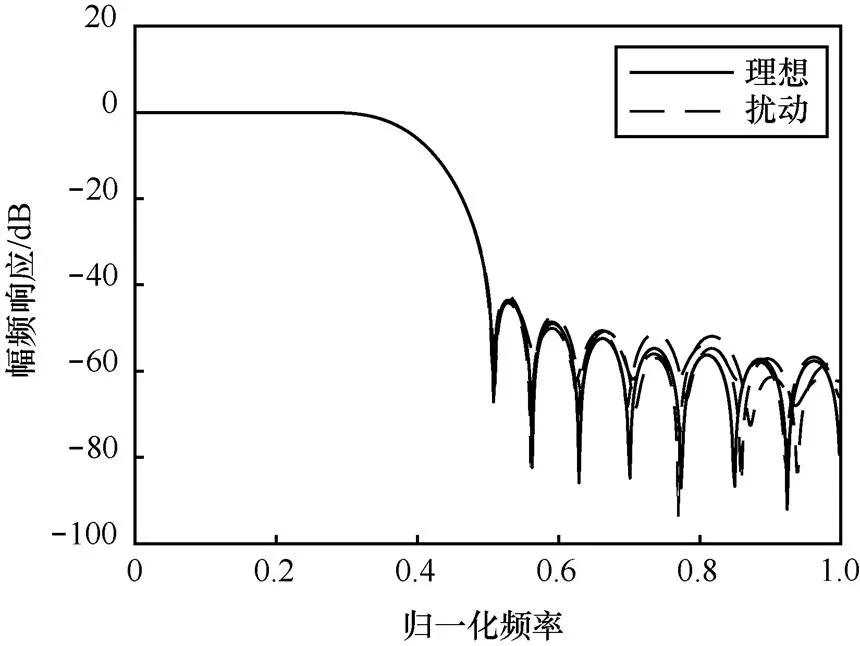
圖5 狀態空間實現下濾波器的幅頻響應變化

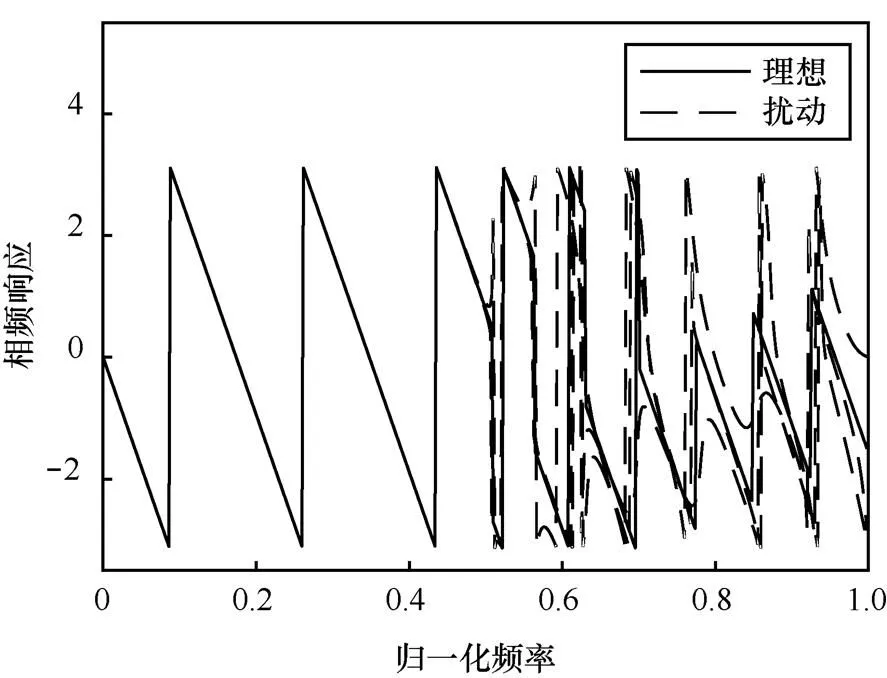
圖6 狀態空間實現下濾波器的相頻響應變化

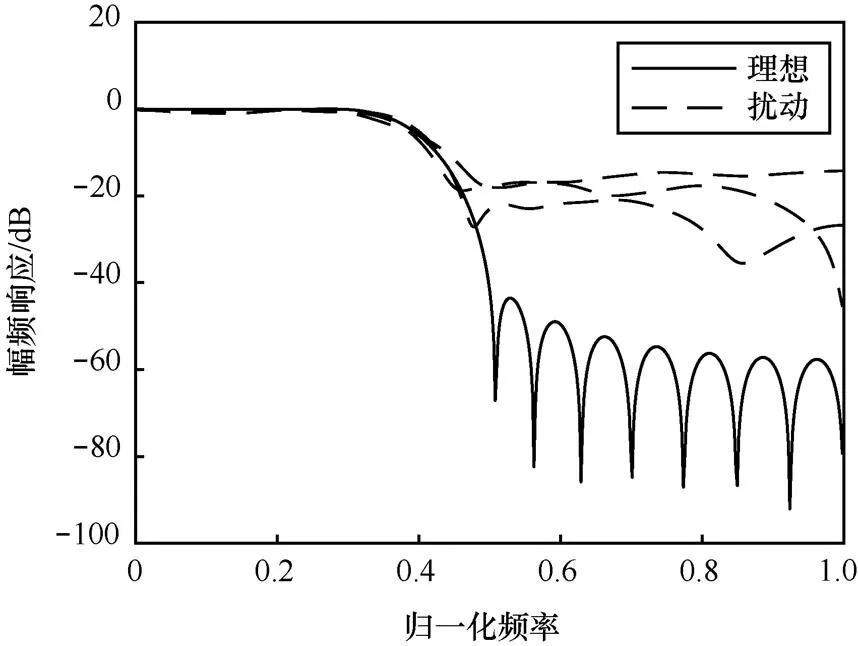
圖7 狀態空間實現下濾波器的幅頻響應變化

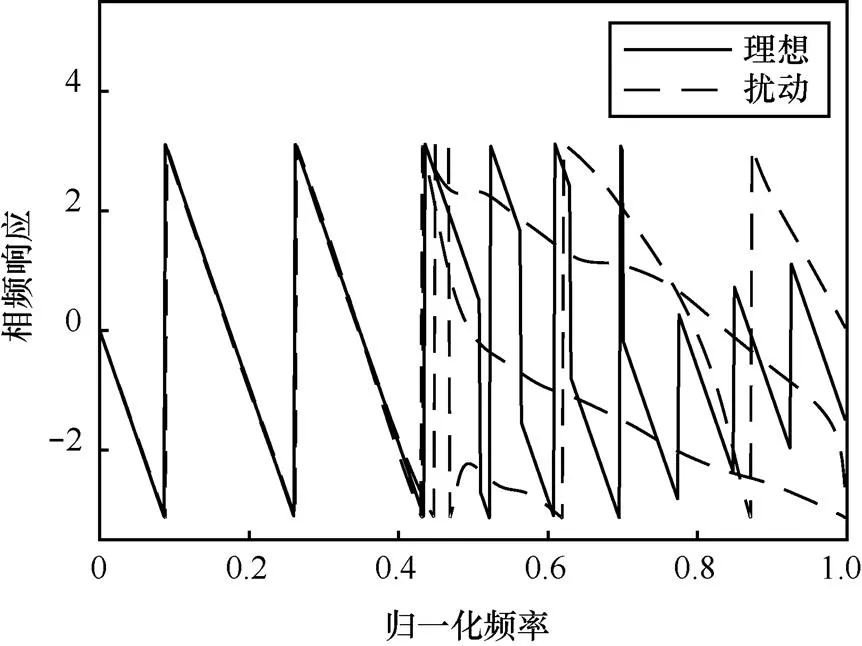
圖8 狀態空間實現下濾波器的相頻響應變化

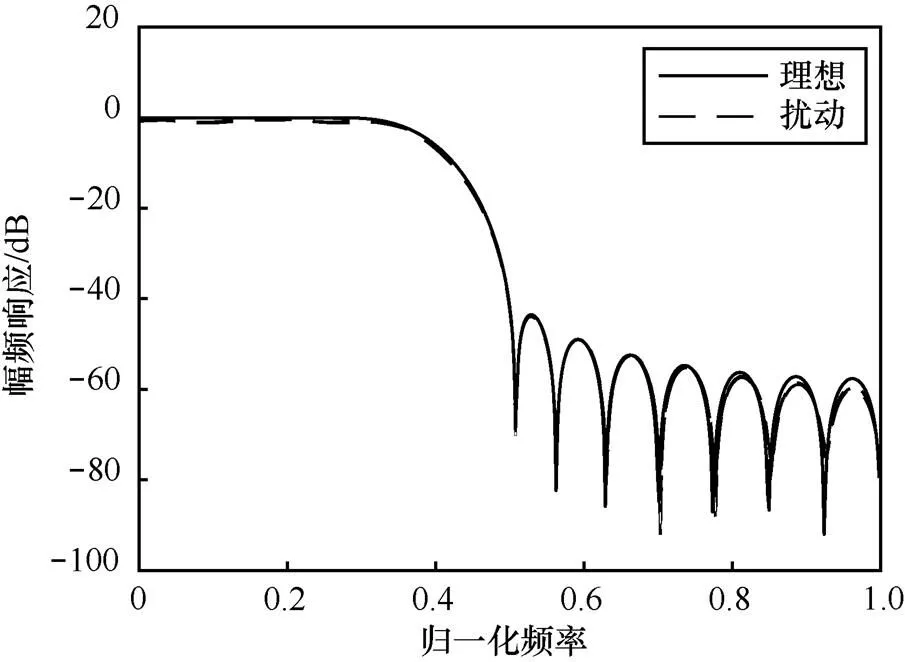
圖9 狀態空間實現下濾波器的幅頻響應變化

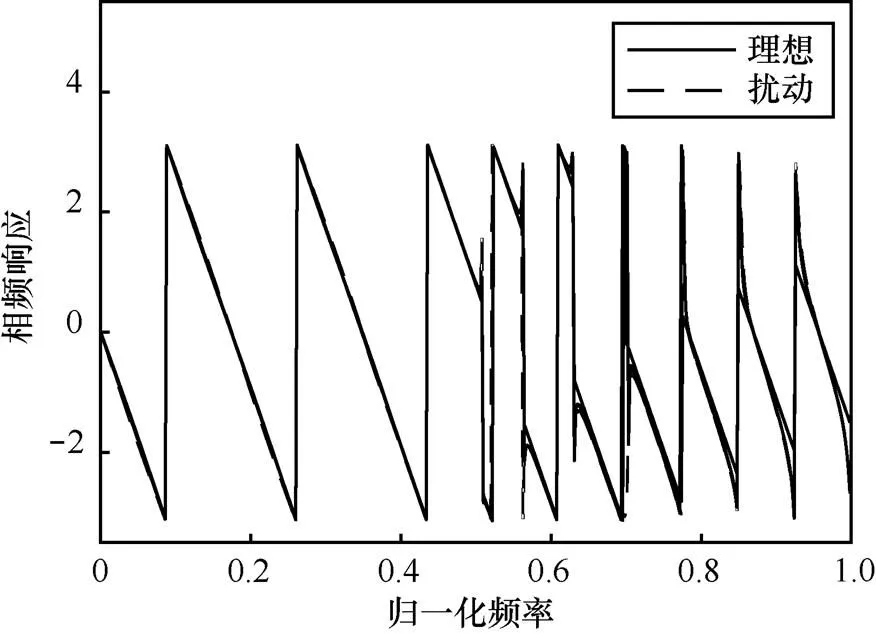
圖10 狀態空間實現下濾波器的相頻響應變化

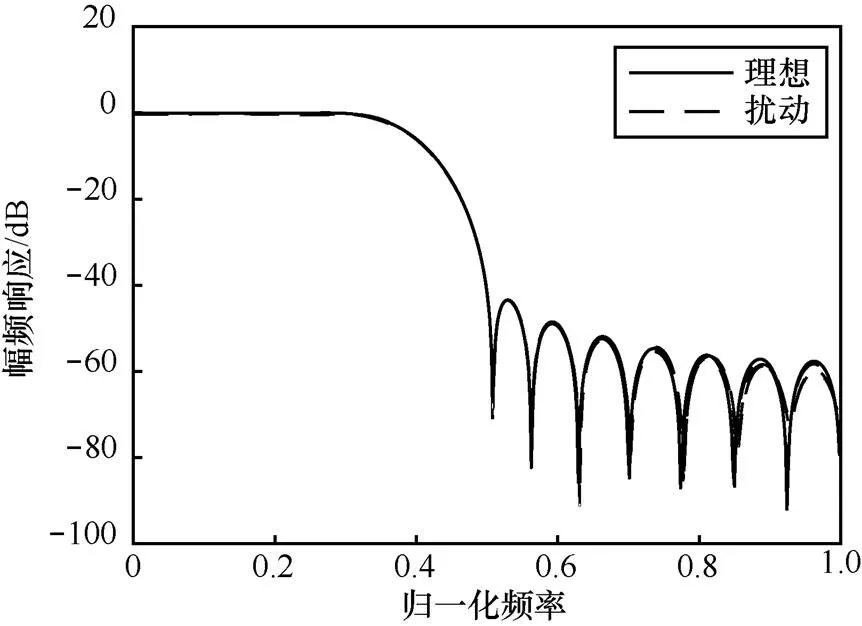
圖11 狀態空間實現下濾波器的幅頻響應變化

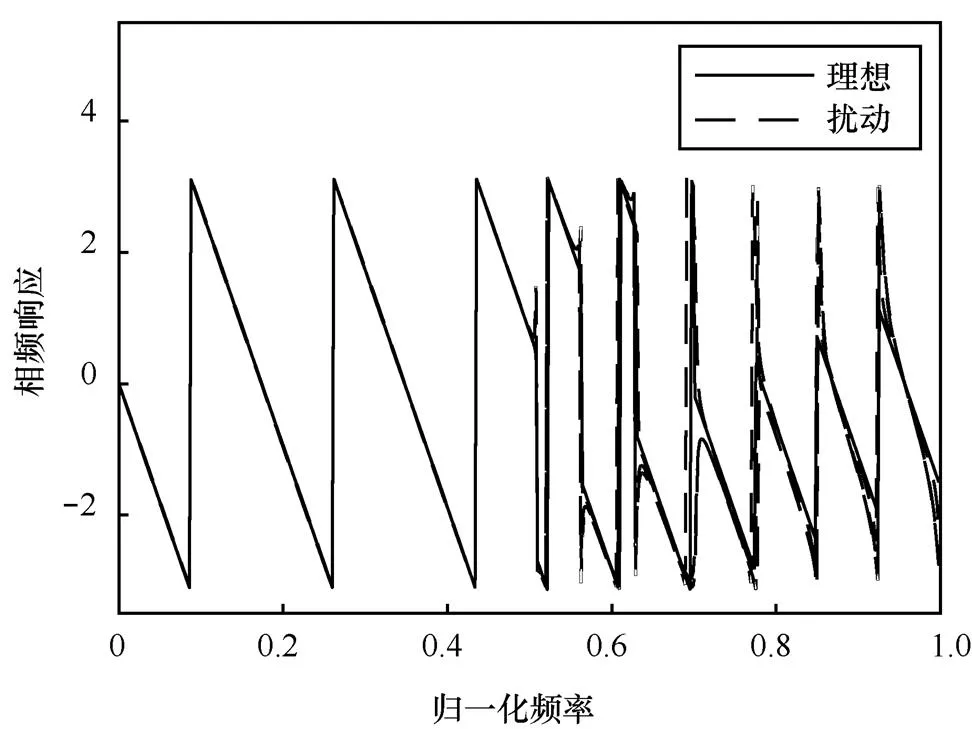
圖12 狀態空間實現下濾波器的相頻響應變化

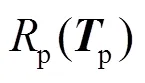
6.2 系數量化下的靈敏度分析

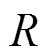
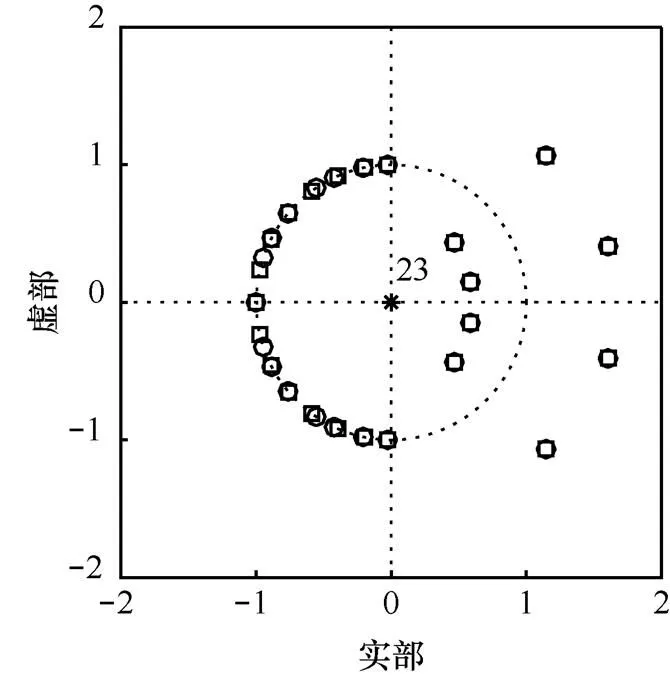
圖13 狀態空間實現R下濾波器的零極點分布比較（Bc=10 bit）

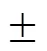
圖14 幅頻響應比較（Bc=10 bit）實線-理想；虛線-R；

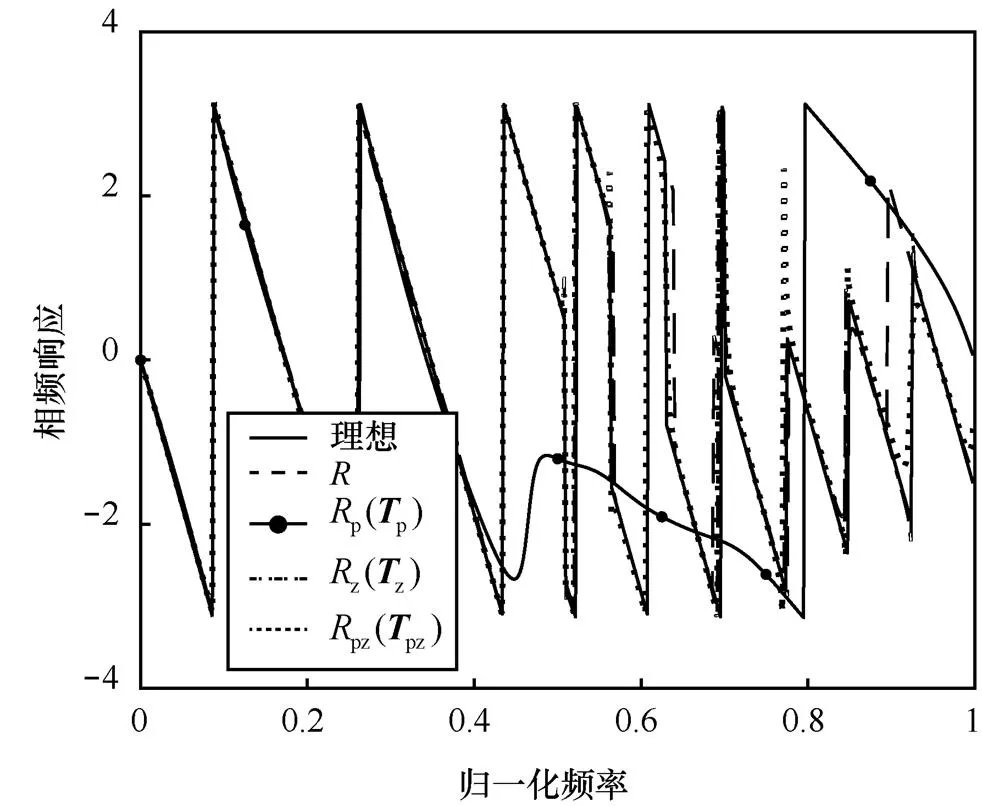
圖15 相頻響應比較（Bc=10 bit）實線-理想；虛線-R；

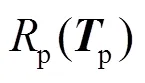
7 結束語

本文基于狀態空間實現結構討論FIR濾波器的零極點靈敏度，引用廣義特征向量對虧損系統矩陣的特征值進行擾動分析，推導出極點靈敏度表達式，并提出FIR濾波器極點、零點及加權零極點靈敏度的優化方案。數值實例表明，由于系統矩陣的虧損性使FIR濾波器極點敏感于系數變化，零極點位置偏移會影響濾波器的頻響特性，仿真結果驗證了所提方案的有效性，即優化實現能夠降低濾波器零極點的靈敏度。

[1] TAVSANOGLU V, THIELE L. Optimal design of state-space digital filters by simultaneous minimization of sensitivity and round off noise[J]. IEEE Transactions on Circuits and Systems, 1984, 31(10): 884-888.

[2] YAN W Y, MOORE J B. On-sensitivity minimization of linear state-space systems[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1992, 39(8): 641-648.

[3] LI G, GEVERS M, SUN Y X. Performance analysis of a new structure for digital filter implementation[J]. IEEE Transactions on Circuits Systems I: Fundamental Theory and Applications, 2000, 47(4): 474-482.

[4] WILLIAMSON D. Round off noise minimization and pole-zero sensitivity in fixed-point digital filters using residue feedback[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(5): 1210-1220.

[5] LI G. On pole and zero sensitivity of linear systems[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1997, 44(7): 583-590.

[6] 徐巍華, 吳俊, 褚健. 有限字長數字控制器的一種極點靈敏度優化結構[J]. 控制理論與應用, 2000, 17(4): 613-618.

XU W H, WU J, CHU J. A class of pole sensitivity optimization structures of an FWL digital controller[J]. Control Theory and Applications, 2000, 17(4): 613-618.

[7] LI G, LIM Y C, HUANG C G. Very robust low complexity lattice filters[J]. IEEE Transactions on Signal Processing, 2010, 58 (12): 6093-6104.

[8] 于愛華, 黃朝耿, 李剛, 等. 一種新型低復雜度的IIR格型濾波器[J]. 電子學報, 2013, 41(9): 1703-1709.

YU A H, HUANG C G, LI G, et al. A new class of low complexity IIR lattice filters[J]. Acta Electronica Sinica, 2013, 41(9): 1703-1709.

[9] MANTEY P. Eigenvalue sensitivity and state-variable selection[J]. IEEE Transactions on Automatic Control, 1968, 13(3): 263-269.

[10] SKELTON R E, WAGIE D A. Minimal root sensitivity in linear systems[J]. Journal of Guidance Control and Dynamics, 1984, 7(5): 570-574.

[11] GEVERS M, LI G. Parameterizations in control, estimation and filtering problems: accuracy aspects[M]. New York: Springer-Verlag, 1993.

[12] HINAMOTO T, DOI A, LU W S. Weighted pole and zero sensitivity minimization for state-space digital filters[C]//2015 IEEE International Symposium on Circuits and Systems (ISCAS). 2015: 2193-2196.

[13] HINAMOTO T, DOI A, LU W S. Minimization of weighted pole and zero sensitivity for state-space digital filters[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(1): 103-113.

[14] 徐濤, 于瀾, 鞠偉, 等. 計算虧損系統模態靈敏度的逐層遞推演算方法[J]. 力學學報, 2008, 40(2): 281-288.

XU T, YU L, JU W, et al. Recursive solution on layer after layer for sensitivity analysis of modes on defective linear vibration system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(2): 281-288.

[15] 陳塑寰, 徐濤, 韓萬芝. 線性振動虧損系統的矩陣攝動理論[J]. 力學學報, 1992, 24(6): 747-753.

CHEN S H, XU T, HAN W Z. Matrix perturbation for linear vibration defective systems[J]. Acta Mechanica Sinica, 1992, 24(6): 747-753.

Analysis and optimal realization of pole-zero sensitivity for FIR digital filters

ZHUANG Ling, MA Jingyi, WANG Guangyu, GUAN Juan

Chongqing Key Lab of Mobile Communications Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

Aiming at the deviation of pole and zero in filters which caused by the finite word length (FWL) effects, the sensitivity of pole and zero for FIR digital filters to coefficient errors was studied based on the state-space model. Unlike the IIR filter, the system matrix in state-space model of the FIR filter was defective. A set of generalized eigenvectors of defective matrix was introduced to analyze the pole sensitivity and derive the measure expression, and optimal realizations with respect to pole-zero sensitivity for FIR filters were proposed by finding optimal transformation matrices according to the similarity transformation theory. Theoretical analysis and simulation experiments show that the poles of a FIR filter are more sensitive to coefficient errors, and the proposed optimal realizations can reduce the sensitivity.

FIR digital filter, state-space realization, pole and zero sensitivity, defective matrix, generalized eigenvector

TN713.7

A

莊陵（1978-），女，重慶人，博士，重慶郵電大學副教授，主要研究方向為通信與信息處理多載波技術、濾波器組理論。

馬靖怡（1993-），女，陜西漢中人，重慶郵電大學碩士生，主要研究方向為濾波器結構設計、多載波濾波器組技術。

王光宇（1964-），男，貴州興義人，博士，重慶郵電大學教授，主要研究方向為高速多載波通信理論。

關鵑（1991-），女，山西運城人，重慶郵電大學碩士生，主要研究方向為移動通信多載波調制技術、濾波器組理論。

2018?01?09；

2018?05?20

中興5G高速連續接入技術方案與試驗系統研發基金資助項目（No.2016ZX03001010-004）

10.11959/j.issn.1000?436x.2018167

The Research and Development Project of ZTE 5G High-Speed Continuous Access Technology and Testing System (No. 2016ZX03001010-004)