集合、函數、導數核心考點B卷參考答案
一、選擇題

二、填空題
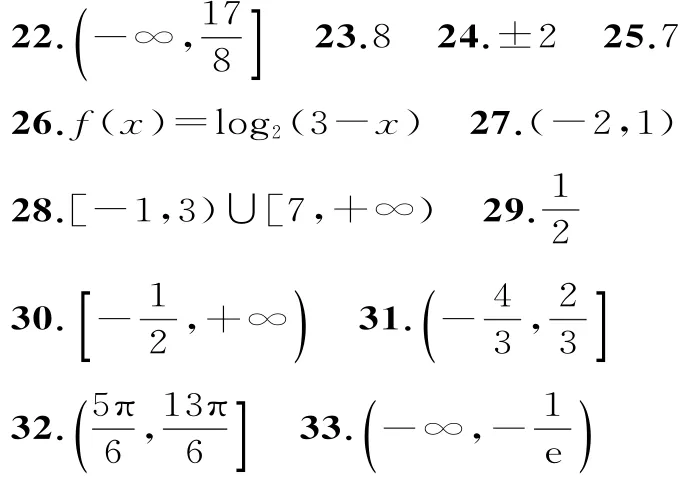
三、解答題
3 4.(1)依題意得(m-1)2=1?m=0或m=2,當m=2時,f(x)=x-2在(0,+∞)上單調遞減,與題設矛盾,舍去,所以m=0。
(2)由(1)得f(x)=x2,當x∈[1,2)時,f(x)∈[1,4),即A=[1,4)。
當x∈[1,2)時,g(x)∈[2-k,4-k),即B=[2-k,4-k),若命題p是q成立的
3 5.(1)設f(x)=a x2+b x+c,由f(0)=1得c=1,所以f(x)=a x2+b x+1,所以f(x+1)=a(x+1)2+b(x+1)+1=a x2+(2a+b)x+a+b+1,所以f(x+1)-f(x)=a x2+(2a+b)x+a+b+1-a x2-b x-1=2a x+a+b。因為f(x+1)-f(x)=2x,所以2a x+a+b=2x,所以2a=2且a+b=0,所以a=1,b=-1,所以f(x)=x2-x+1。
(2)若方程f(2x)=2x+a在(-∞,2]上有兩個不同的解,即a=(2x-1)2在(-∞,2]上有兩個不同的解,令t=2x,則0<t≤4,令g(t)=(t-1)2,畫出函數g(t)和y=a的圖像,如圖1所示,故0<a<1。
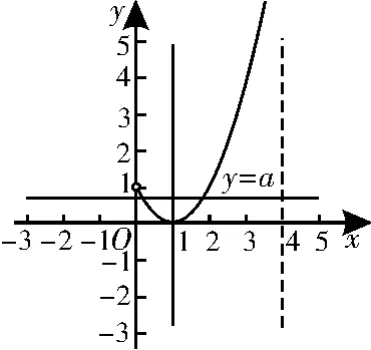
圖1
3 7.(1)函數f(x)=[a x2-(4a+1)x+4a+3]ex的導數為f'(x)=[a x2-(2a+1)·x+2]ex。由題意可得曲線y=f(x)在點(1,f(1))處的切線斜率為0,即(a-2a-1+2)e=0,解得a=1。
(2)由已知得f'(x)=[a x2-(2a+1)x+2]ex=(x-2)(a x-1)ex。
若a=0,則x<2時,f'(x)>0,f(x)遞增;x>2時,f'(x)<0,f(x)遞減。在x=2處f(x)取得極大值,不符合題意。
令h(x)=x2-(a+2)x+al nx+2a+2,等價于函數h(x)在(0,2]內與x軸只有唯
①當a<0時,h(x)在(0,1)上遞減,在(1,2]上遞增。當x→0時,h(x)→+∞,要使函數h(x)在(0,2]內與x軸只有唯一的交點,所以h(1)=0或h(2)<0,所以a=-1
②當h(1)=a+1>0,當x→0時,h(x)→-∞。因為h(e-4)=e-8-e-4-2<0,h(1)=a+1的交點。
③當a=2時,h(x)在(0,2]上遞增。因為h(e-4)=e-8-e-4-2<0,f(2)=2+l n 2>0,所以h(x)在(0,2]內與x軸只有唯一的交點。
(2)f(x)=(2-a)(x-1)-2 l nx(a∈所以切線方程為y-1=(1-a)(x-1)。
因為曲線g(x)在點(1,g(1))處的切線過點(0,2),所以2-1=-1+a,解得a=2。
所以或0<a≤2。
3 9.(1)g(x)=f(x)+x=(3-a)x-2+a-2 l nx(x>0),g(1)=1。
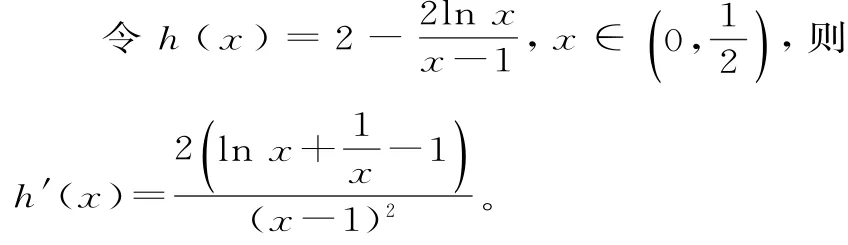
4 0.(1)當n=0時,得h'(x)=(ex-
當x∈(-1,l nm)時,h'(x)<0,h(x)單調遞減;當x∈(l nm,+∞)時,h'(x)>0,h(x)單調遞增。
所以函數h(x)在(-1,+∞)上有最小值h(l nm)=m-ml nm,令m-ml nm>0,
令F(x)=ex(3x-4)+x+4,則F(0)=0,且F'(x)=ex(3x-1)+1,F'(0)=0。
令G(x)=F'(x),則G'(x)=ex(3x+2),因為x≥0,所以G'(x)>0。
導函數F'(x)在[0,+∞)上單調遞增,于是F'(x)≥F'(0)=0,從而函數F(x)在[0,+∞)上單調遞增,即F(x)≥F(0)=0。
故ex(3x-4)+x+4≥0,即r(x)≥1。
當a<0時,f'(x)<0,知f(x)在(0,+∞)上是遞減的;當a>0時,f'(x)=遞減的,在(a,+∞)上遞增的。
由a=e2得x1∈(0,e),x2∈(e,+∞)。
由f(2 e)=2-2 l n2>0及f(x2)=0,得x2<2 e,即x2∈(e,2 e)。
欲證x1+x2>2 e,只要x1>2 e-x2,注意到f(x)在(0,e)上是遞減的,且f(x1)=0,只要證明f(2 e-x2)>0即可。
綜上,x1+x2>2 e。

