體驗式教學模式在中職數學課堂中的實踐與探索

金鳳慧

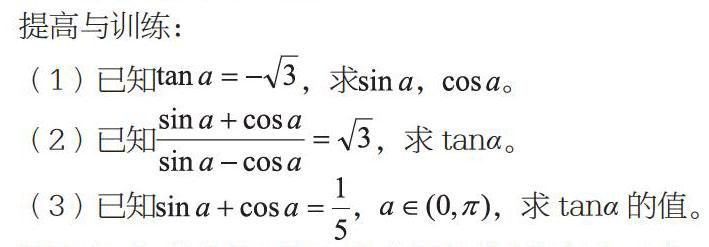
中等職業學校是我國教育大家庭中的一個重要成員，職校的培養目標是為社會和經濟發展培養技能型人才和高素質勞動者。職校生從小學到現在，整整學了9年的數學，但直到現在，他們往往還沒弄清楚數學有什么作用，對數學也沒有多大的興趣，最終導致失去學習的信心。職業學校，顧名思義，是以學專業技術為主的，數學作為一門基礎科目往往不受重視，但是實質上，數學常常滲透在專業理論的方方面面，比如電工基礎上就涉及了三角函數的知識，機械制圖上就涉及了立體幾何的知識。中職教師首先要考慮的是如何激發職業學校學生學習數學的興趣。

近年來，我校為提高教學質量做了不少有益的嘗試，并逐步確立了以“體驗式教學模式”為核心的課改理念。

體驗式模式是指教師以一定的理論為指導，讓學生親身去體驗、感知新知，并通過檢測反饋得到交流體驗，從而使學生成為課堂真正的主人的教學模式。體驗式教學模式的主旨在于以創設情境、任務引領教學，通過師生雙邊活動的方式完成學習。主要過程為：情境創設、情感體驗——任務引領、實踐體驗——檢測反饋、交流體驗——作業布置、延伸體驗。

下面以“同角三角函數的基本關系式”的教學為例，分析體驗式教學模式的實施過程。

一、情境創設，情感體驗

首先，我以提問的方式提出以下三個問題，讓全班學生思考：

（1）[O，2π]之間特殊角的三角函數值分別是多少？

設計意圖：復習該知識點的目的是為了讓學生觀察表格中正弦值與余弦值、切值和弦值等數字之間的關系，從而猜測出同角三角函數的基本關系式。

（2）角a的正弦函數、余弦函數和正切函數的定義如何表示？

設計意圖：復習該知識點的目的是為了讓學生從三角函數的定義中探索它們之間存在一定的聯系，從而得出同角三角函數的基本關系式的證明方法。

（3）各象限角的三角函數值的正負號的判斷口訣是什么？

設計意圖：復習此知識點的目的是為了突破本節課的難點，在計算過程中遇到開方時，可借助口訣進行判斷。

經過學生證明后教師總結：①兩大基本關系;②提出注意點：公式是對任何角都有意義;公式中指的是同一個角;平方關系開方時要注意正負號。

二、任務引領，自主體驗

任務一：已知sina=-3/5，且a是第三象限的角，求cosa和tana的值。

分析：知道正弦函數值，可以利用平方關系，求出余弦函數值，然后利用商數關系，求出正切函數值。

解：由sin2a+cos2a=l，可得cosa=±√1一sin2a。

又因為a是第三象限的角，故cosa<0。

所以cosa=

任務一先由學生獨立思考后再一起來回答，教師板書配合;之后提出注意點，并對解題過程的規范性提出要求;小結已知一個角的正弦值，求另外兩個三角函數值的方法。（簡稱“知一求二”）

設計意圖：通過例題的求解，讓學生加深對關系式的理解，并進一步掌握關系式在解題中的應用，突出本節課的重點。通過板書，培養學生解題規范的習慣。

變式一：如果把上例中的“改為第四象限的角，或者去掉該條件，或者將正弦值改為余弦值，結果會產生什么變化？把此題作為本節課的第一個課堂練習題。提出此問題后，學生先自己思考，然后教師做引導：對此問題需要進行討論。討論時，首先根據已知條件sma=-4/5，可以確定角a為第三或第四象限的角，然后就a為第三象限的角或a為第四象限的角分別求出cosa和tana，由兩個學生在黑板上板書出結果，并作點評。

設計意圖：引導學生自主探索，親自體驗解題思路的形成過程，學會分析問題、解決問題的方法，體現分類的思想方法，注重解題方法和步驟，同時使本節課的難點得以突破。

任務二：已知tana=3/4

分析：觀察已知與所求，利用商數關系，將所求的式子中“弦”變成“切”的形式。只要將分子分母同時除以余弦，變成關于切的一個關系式。

設計意圖：由切求弦，體現了化切為弦或者弦化切的通法，或者構建方程組，體現了方程組的思想。

變式二：已知條件不變，求：sinacosa+2cos2a。

設計意圖：巧用“1”的變化求三角函數式子的值，是為了更好地加強學生對同角三角函數基本關系式的理解和記憶，體現三角函數的妙用。

任務三：已知sina+cosa=1/2，求sina·cosn。

分析：觀察前后式子，找出正弦與余弦之間的內在聯系。利用平方關系整體求出結果。

解：sina+cosa=1/2平方后變為1+2 sina·cosa=1/4，

故sina·cosa=-3/8。

設計意圖：讓學生學會觀察和前后聯系并能靈活運用公式，體驗數學中“整體”的思想。在解題過程中，讓學生感受到數學的奇妙，慢慢培養出對數學的學習興趣。

變式三：已知條件不變，求：（l）sin3a+cos3a; （2）sina-cosa。

設計意圖：通過本例題強化學生的整體思想，開方時注意正負號。

三、反饋提高，實踐體驗

本節課通過對特殊角的三角函數值的觀察找出規律，進而嘗試用三角函數的定義推導并證明出同角三角函數之間的關系，最終得到同角三角函數的兩個基本關系式。通過例題和課堂練習介紹了公式在實際生活、求值和專業知識等方面的應用。兩個基本關系式是三角函數的基礎，希望同學們加深理解，靈活運用。

展示歷年高考關于“三角函數求值”的考試情況分析，同時通過多媒體展示本節課的課堂測驗：

1.（2018年高考題）已知x∈（O，π），且cosx=4/5，求tanx。

2.（2017年高考題）已知a=（cosa，sina），b=（2，1），若a·b=1，則cosa=

。

設計意圖：所選的練習題從簡單到復雜，從特殊到一般，層層深入，滿足了學生的不同需求。測驗緊扣高考考綱，消除了對高考題的恐懼，進而產生一種成就感，激發了學生的學習熱情。

四、作業布置，延伸體驗

提高與訓練：

（1）已知tana=一√3，求sina，cosa。

（2）已知

，求tana 。

（3）已知sina+cosa=1/5，a∈（O，π），求tana的值。

設計意圖：作業設置緊扣本節課的教學目標和重點。（知一求二，巧化“1”，方程組的思想）

五、課后反思，教學相長

采用啟發式教育和小組討論的方法，可以激發學生的學習熱情，能夠使絕大多數的學生主動參與進來。在教學過程中采用講練結合法，加深對知識的記憶與掌握，在實踐中發現自己的不足，課后就可以有重點地去練習。

在整個教學過程中發現，有些學生不怎么會靈活運用同角三角函數的基本關系式，一部分學生感到困難，本人借助多媒體演示、例題講解、鞏固練習、小組討論后，難點基本得以突破。通過課堂檢測能反饋學生的掌握情況，及時調整教學方法。本堂課的教學體現了觀察和想象能力的重要性，在以后的教學中要注意培養學生這方面的能力。