熱傳導(dǎo)高溫服裝設(shè)計(jì)研究

王國慶　武佳琪　武偉娜

摘要：隨著時代的進(jìn)步和經(jīng)濟(jì)的快速發(fā)展，高溫作業(yè)受到了各行業(yè)的廣泛關(guān)注，同時高溫作業(yè)專用服裝的設(shè)計(jì)與研究也成為了熱門問題。為降低研發(fā)成本，縮短開發(fā)周期，本文在環(huán)境溫度為75?C、II層厚度為6 mm、IV層厚度為5 mm、工作時間為90分鐘的情況下進(jìn)行實(shí)驗(yàn)，通過熱傳導(dǎo)模研究不同環(huán)境溫度下的假人皮膚外側(cè)的溫度變化情況，使用matlab軟件進(jìn)行數(shù)據(jù)計(jì)算分析，并建立熱傳導(dǎo)模型，得到皮膚溫度與時間的擬合關(guān)系，繪制出整個傳熱過程的溫度三維分布圖。

關(guān)鍵詞：熱傳導(dǎo);Matlab;溫度三維分布圖

1 引言

在高溫環(huán)境下工作時，高溫作業(yè)工作服裝能夠盡可能的減少對人體的傷害。這種特殊服裝通常由三層材料組成，分別記為I、II、III層，I層與外部環(huán)境接觸，III層與皮膚之間有間隙，這個間隙空間為IV層。在現(xiàn)代學(xué)者的實(shí)驗(yàn)過程中，一般都會將體溫控制在37?C的人體模型置于高溫環(huán)境中，從而測量人體模型皮膚外部的溫度。

2 數(shù)據(jù)預(yù)處理

本文通過對高溫服裝制造廠的探訪，收集相關(guān)數(shù)據(jù)并進(jìn)行處理，可以發(fā)現(xiàn)：初始時刻的人體溫度為37℃，在1745s時體溫保持48.08℃且不發(fā)生變化。進(jìn)而，對從初始時刻到1745s這段時間的數(shù)據(jù)進(jìn)行處理，利用Matlab進(jìn)行六階擬合最為合適^[1]，得到人體皮膚溫度與時間的關(guān)系圖像，如圖1所示。

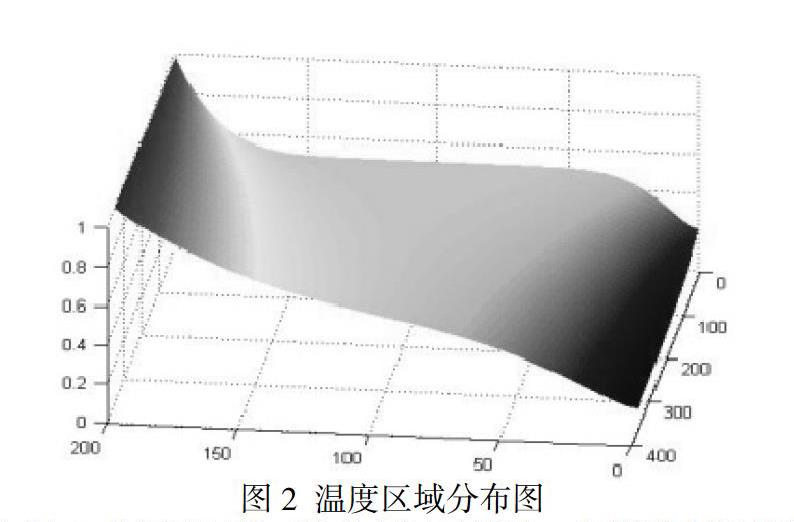
綜合考慮上述兩種不同的傳導(dǎo)模型，結(jié)合皮膚溫度與時間的數(shù)據(jù)擬合方程，利用MATLAB仿真得到最終的溫度區(qū)域分布圖，如圖2所示。

由圖2的溫度區(qū)域三維分布圖可得到：對應(yīng)不同的時間和材料層之間的距離，相對應(yīng)的溫度也會不同，其中溫度由深紅色到藍(lán)色，顏色越深，溫度越高。

3.2有限差分法求解方程

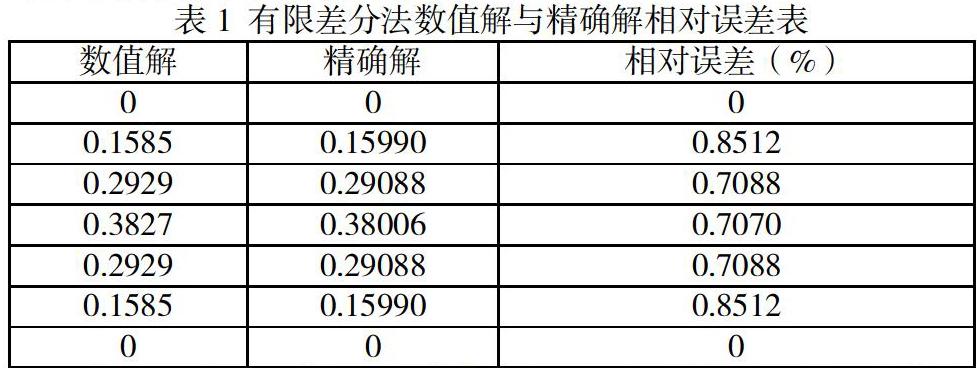
當(dāng)使用有限差分對偏微分方程進(jìn)行離散化時，方法是多種多樣的^[5]。此外，對于相同的偏微分方程，可以建立不同的差分方程。針對上述實(shí)例，采用t和x的正向差分，建立經(jīng)典顯示格式的差分方程，以取代原來的偏微分方程。采用有限差分格式，逐層進(jìn)行計(jì)算。如果需要考慮兩級差分格式，則使用i+1層上計(jì)算的值。計(jì)算第i層時的誤差（包括i=0的情況，但由于初始數(shù)據(jù)的不精確性）必須影響第i+1層的值^[8]。所以必須分析這個誤差傳播。誤差的影響不會以掩蓋差分格式的解決方案出現(xiàn)，即所謂的穩(wěn)定性。在此基礎(chǔ)上，用矩陣法分析了上述差分方程的穩(wěn)定性。本文使用有限差分法數(shù)值解與精確解的相對誤差表。

由表1可知最大的相對誤差為0.8512%，因此可認(rèn)為熱傳導(dǎo)方程的數(shù)值解是穩(wěn)定收斂的。

4 結(jié)束語

本文建構(gòu)熱傳導(dǎo)模型能夠與實(shí)際緊密聯(lián)系，模型更加貼近實(shí)際，有很好的通用性和推廣性，并且利用Matlab繪制的溫度分布三維模型，其可視化界面形象逼真，操作簡便，便于分析與應(yīng)用。熱傳導(dǎo)模型可在多個領(lǐng)域進(jìn)行應(yīng)用和推廣，主要應(yīng)用于從事高溫作業(yè)的相關(guān)領(lǐng)域，熱傳導(dǎo)模型可用來研究高溫工作服，使相關(guān)工廠的工作人員避免不必要的傷害，同時也可以減少對消防人員造成的損傷。當(dāng)然，熱傳導(dǎo)模型還可以應(yīng)用于各方面與高溫作業(yè)有關(guān)的領(lǐng)域，有很好的推廣性。

參考文獻(xiàn)：

[1] 劉春鳳.數(shù)值計(jì)算方法[M].高等教育出版社，2017

[2] 王朔中，克達(dá)爾，秦川，等.應(yīng)用熱傳導(dǎo)模型的偏微分方程圖像修復(fù)[J].上海大學(xué)學(xué)報(bào)（自然科學(xué)版），2007，13（4）：331-336.

[3] 吳孟達(dá).數(shù)學(xué)建模教程[M].高等教育出版社，2011.

[4] 過增元，朱宏曄.熱質(zhì)的運(yùn)動和傳遞-熱子氣的守恒方程和傅立葉定律[J].工程熱物理學(xué)報(bào)，2007，28（1）：86-88.

[5] 楊杰.基于人體-服裝-環(huán)境的高溫人體熱反應(yīng)模擬與實(shí)驗(yàn)研究[D].清華大學(xué)，2016.

（作者單位：華北理工大學(xué)理學(xué)院）