表貼式永磁電機齒槽轉矩解析法比較研究

倪有源，王 磊

(1.合肥工業大學，合肥 230009;2.安徽大學高節能電機及控制技術國家地方聯合工程實驗室，合肥 230601)

0 引 言

永磁電機相比于傳統的電勵磁電機具有結構簡單、質量輕及效率高等優勢[1]，從而廣泛運用在各種領域中。但是在一些特殊的領域中，要求轉矩脈動低。而轉矩脈動是永磁電機內在的缺陷，會產生振動和噪聲。轉矩脈動主要來源于齒槽轉矩，齒槽轉矩是由永磁體與電樞槽相互作用而產生的[2]。

研究齒槽轉矩具有重要的意義。國內外學者展開了廣泛的研究，也提出了許多減小齒槽轉矩的方法，如采用槽數與極數的配合[3-4]，通過定子加輔助槽[5-6]，選取合適的極弧系數[6-7]，改變永磁體的形狀[8-9]以及利用轉子偏心的辦法[6,9]等。

齒槽轉矩的計算方法通常分為兩類：有限元法和解析法。對齒槽轉矩的研究大多采用的是有限元法，雖然計算結果精度高，但是需要大量的計算時間，而且不適合進行優化分析。解析法是一種快速得到齒槽轉矩的有效方法，并且從設計方面能直接得出影響齒槽轉矩的因素。解析法主要包括能量法[5,10-12]和麥克斯韋應力張量法[13-16]。

本文分析了計算齒槽轉矩的4種模型。其中模型A是利用理想化的氣隙磁密計算齒槽轉矩的簡化模型。模型B是通過先求解拉普拉斯方程和準泊松方程，獲得氣隙磁密解析式，然后計算齒槽轉矩。模型C是先利用保角變換獲得不同位置處精確的相對磁導，再計算齒槽轉矩，與利用能量法的其它模型相比，該模型得到的齒槽轉矩更接近于實際結果。模型D是運用麥克斯韋應力張量法計算齒槽轉矩。

1 解析模型分析

表貼式永磁電機的分析模型如圖1所示。圖1中Rs為定子內半徑，Rr為永磁內半徑，Rm為永磁體外半徑。本文分析齒槽轉矩的4種解析模型，是基于如下考慮：假設鐵心的磁導率為無窮大；θ=0為永磁的中心位置處；永磁材料的磁導率與空氣相同，即μr=1；槽形為直角槽，且假設槽無限深。

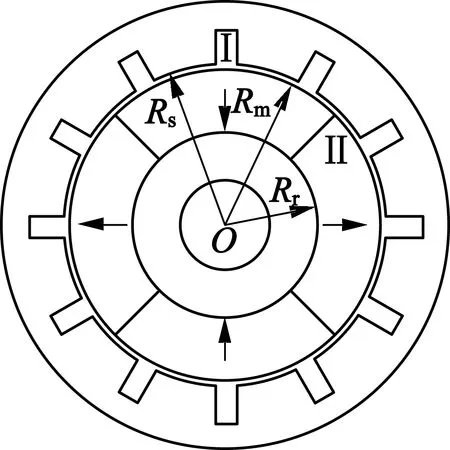
圖1 永磁電機的結構

1.1 模型A

模型A是利用能量法計算齒槽轉矩。根據定義可知[2],齒槽轉矩是由于轉子轉動時電機中能量的變化而產生，且一般鐵心中能量的變化是可忽略的[13]。如果不考慮永磁的能量變化，齒槽轉矩波形的基本特性也不會改變。依據文獻[10]，可得齒槽轉矩：

(1)

式中：α為轉子轉動的位置角度；W表示永磁電機的氣隙中儲存的能量；θ表示沿電機旋轉方向變化的角度；B(θ)為無槽電機的氣隙磁密；G(θ,α) 為氣隙的相對磁導函數。

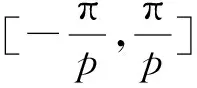
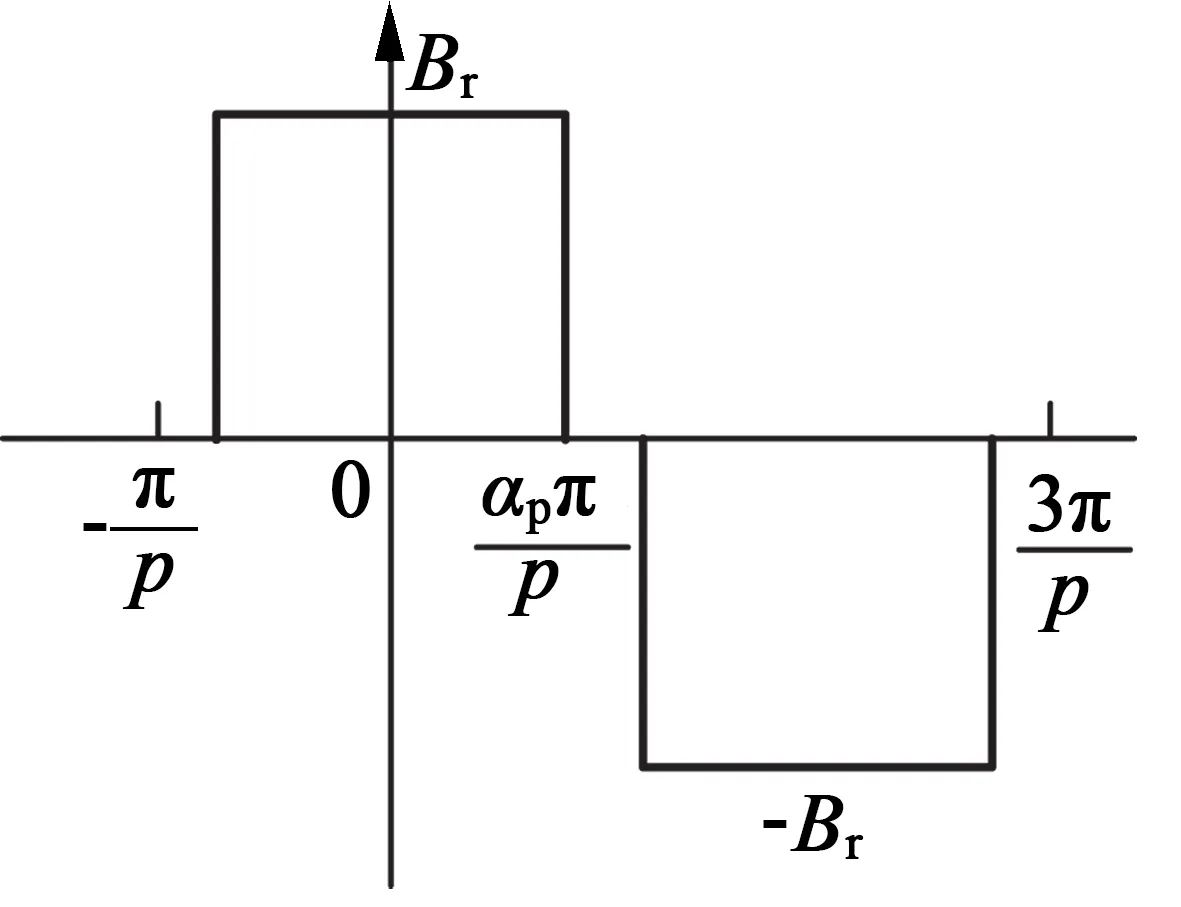
圖2 理想的氣隙磁密分布

(2)

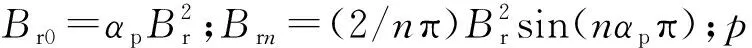
令β=0為一個槽中心的位置。假設磁密通過槽的路徑如圖3所示。磁密在槽中的路徑為四分之一圓，得到一個槽距下有效氣隙長度：

圖3 磁密在槽中的理想路徑

(3)

式中：g為氣隙長度；θ1為槽距角；θ0為槽口角。且θ0和θ1都用弧度。

(4)

再對其進行傅里葉分解，得：

(5)

式中：Ns表示電機定子槽數。

考慮到槽與永磁的相對位置，得β=θ+α。于是得到：

(6)

(7)

將式(5)和式(2)代入式(1)，再利用三角函數的正交性，即式(8)，可得式(9)。

當n≠m時，有：

(8)

(9)

式中：Lef為電機的軸向長度；NL表示槽數與極數的最小公倍數。

模型A運用的是能量法。由于對氣隙磁密進行了簡化，沒有考慮極間漏磁。且磁密在槽中的路徑也是理想化，沒有考慮槽漏磁，因此得到的結果與實際誤差較大。

1.2 模型B

在模型A中，氣隙磁密的波形是理想化的。實際上，精確的氣隙磁密解析式可以通過求解拉普拉斯方程和準泊松方程得到[17]。當定子為無槽結構時，在氣隙區域Ⅰ和永磁區域Ⅱ中，磁感應強度與磁場強度分別滿足：

(10)

式中：BrⅠ,HrⅠ分別為空氣中的磁通密度和磁場強度；BrⅡ，HrⅡ分別是永磁中的磁通密度和磁場強度；M為永磁體的磁化強度。

在二維極坐標下，磁化強度矢量可表示：

M=Mrr+Mθθ

(11)

式中：Mr和Mθ分別為永磁體磁化強度的徑向方向和切向方向的分量。

由于旋轉永磁電機的永磁體一般是徑向充磁的，一對磁極下的磁化強度分布可以寫成分段函數：

(12)

對Mr和Mθ分別進行傅里葉分解，得到：

(13)

根據電磁場理論，對于標量磁位φ，有：

(14)

對于圖1中的氣隙區域Ⅰ和永磁區域Ⅱ，標量磁位分別滿足拉普拉斯方程和準泊松方程，得到：

(15)

(16)

再根據磁場的邊界條件，可得：

(17)

于是，氣隙區域Ⅰ磁密的徑向分量和切向分量分別：

(18)

式中：

令r=Rs，代入式(18)中的BrⅠ(r,θ)，得到式(1)中的B(θ)，對其平方，并計算傅里葉級數，得到：

(19)

將式(19)和式(6)代入式(9)，得到該模型下的齒槽轉矩。與模型A相比，模型B也是運用了能量法。但由于模型B考慮了永磁的極間漏磁，得到的氣隙磁密更接近實際情況，從而得到的齒槽轉矩更接近實際結果。但是磁密在槽中的路徑也為理想情況，因此得到的結果與實際情況還是存在一定的誤差。

1.3 模型C

在計算氣隙磁導時，模型A和模型B都認為磁密通過槽中的路徑如圖3所示。這是為了計算方便，對路徑進行理想化，但與實際存在誤差。因此模型C運用保角變換的方法得到精確的相對磁導函數。

對于圖1的有槽結構永磁電機，相對磁導函數由文獻[18]可以得出：

(20)

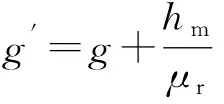
(21)

并且：

(22)

由電磁原理，得相對磁導函數：

(23)

將相對磁導函數寫成傅里葉級數的形式，即：

(24)

然后令r=Rs并代入式(23)，求得相對磁導。對式(24)的兩邊平方，再對其展開傅里葉級數，得：

(25)

將式(19)和式(25)代入式(9)，于是可計算齒槽轉矩，該模型也是運用能量法計算齒槽轉矩。與模型A和模型B相比，模型C運用了保角變換計算相對磁導，而不是假設磁密通過槽的路徑為四分之一圓，于是得到相對磁導更加精確，從而獲得的齒槽轉矩更接近實際情況。

1.4 模型D

除了采用能量法以外，還可以采用麥克斯韋應力張量法計算。運用麥克斯韋應力張量法計算齒槽轉矩的基本條件，是已知氣隙磁密的徑向分量和切向分量。式(18)已給出了表貼式無槽永磁電機的氣隙磁密，而有槽電機的相對氣隙磁導在式(24)中給出，這里就不再贅述。

依據文獻[19]，有槽電機的氣隙磁密可以寫成：

Bs(θ,α,r)=G(θ,r)Bmag(θ,α,r)

(26)

式中：Bmag(θ,α,r)為無槽電機的氣隙磁密，包括徑向分量和切向分量。

根據麥克斯韋應力張量法和文獻[13]，齒槽轉矩表達式：

(27)

式中：Bsr(r,θ)和Bsθ(r,θ)分別為氣隙磁密的徑向分量和切向分量。

為了便于計算，可將式(18)寫成：

(28)

將式(27)和式(22)代入式(25)中，可得：

(29)

(30)

把式(29)和式(30)代入式(27)，可得：

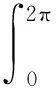
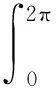
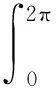
cos(mNsθ)cos(hNsθ)dθ}

(31)

對于式(31)，利用三角函數的正交性，可得：

①如果kp+np-mNs=0，則：

sin[p(k+n)α]

(32)

②如果kp-np+mNs=0或kp-np-mNs=0，則：

sin [p(k-n)α]

(33)

③如果kp+np+mNs-hNs=0或kp+np-mNs+hNs=0或kp+np-mNs-hNs=0，則有：

Brn(r)Bθksin[(k+n)pα]

(34)

④如果kp-np+mNs+hNs=0或kp-np+mNs-hNs=0或kp-np-mNs+hNs=0或kp-np-mNs-hNs=0，則有：

Brn(r)Bθksin [(k-n)pα]

(35)

在式(32)至式(35)中的r，可以為氣隙中任意半徑處，但如果選擇的半徑太接近定子內徑表面時，則計算時會出現問題。因為在這個位置處，利用保角變換計算氣隙的相對磁導時，根據文獻[16]，可以得到氣隙的相對磁導為無窮大。為了避免造成相對磁導無窮大的問題，半徑取為氣隙的中間位置。

2 解析法計算結果及有限元法驗證

一臺3相、4極24槽表貼式永磁電機的主要參數如表1所示。永磁磁化方向為徑向。利用上述建立的各種解析模型，對齒槽轉矩進行分析計算。

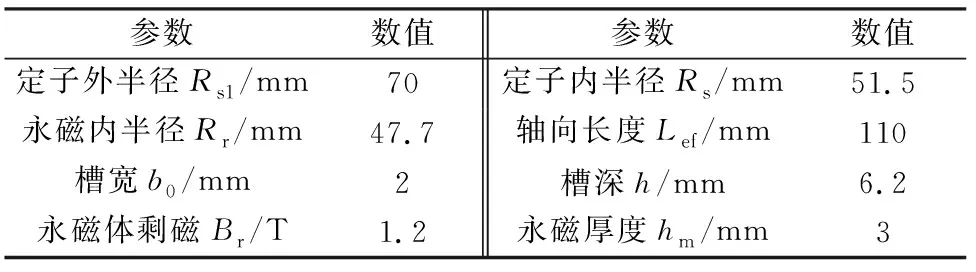
表1 永磁電機的主要參數

當電機的極弧系數αp分別取0.7和0.9時，圖4給出了利用前述的4種模型以及有限元法分別計算得到的齒槽轉矩波形。從圖4中可以得到，解析模型A和解析模型B計算獲得的齒槽轉矩波形與有限元法得到的結果誤差較大。模型C和模型D由于考慮了極間漏磁和槽漏磁，得到的齒槽轉矩波形更接近有限元法的計算結果。

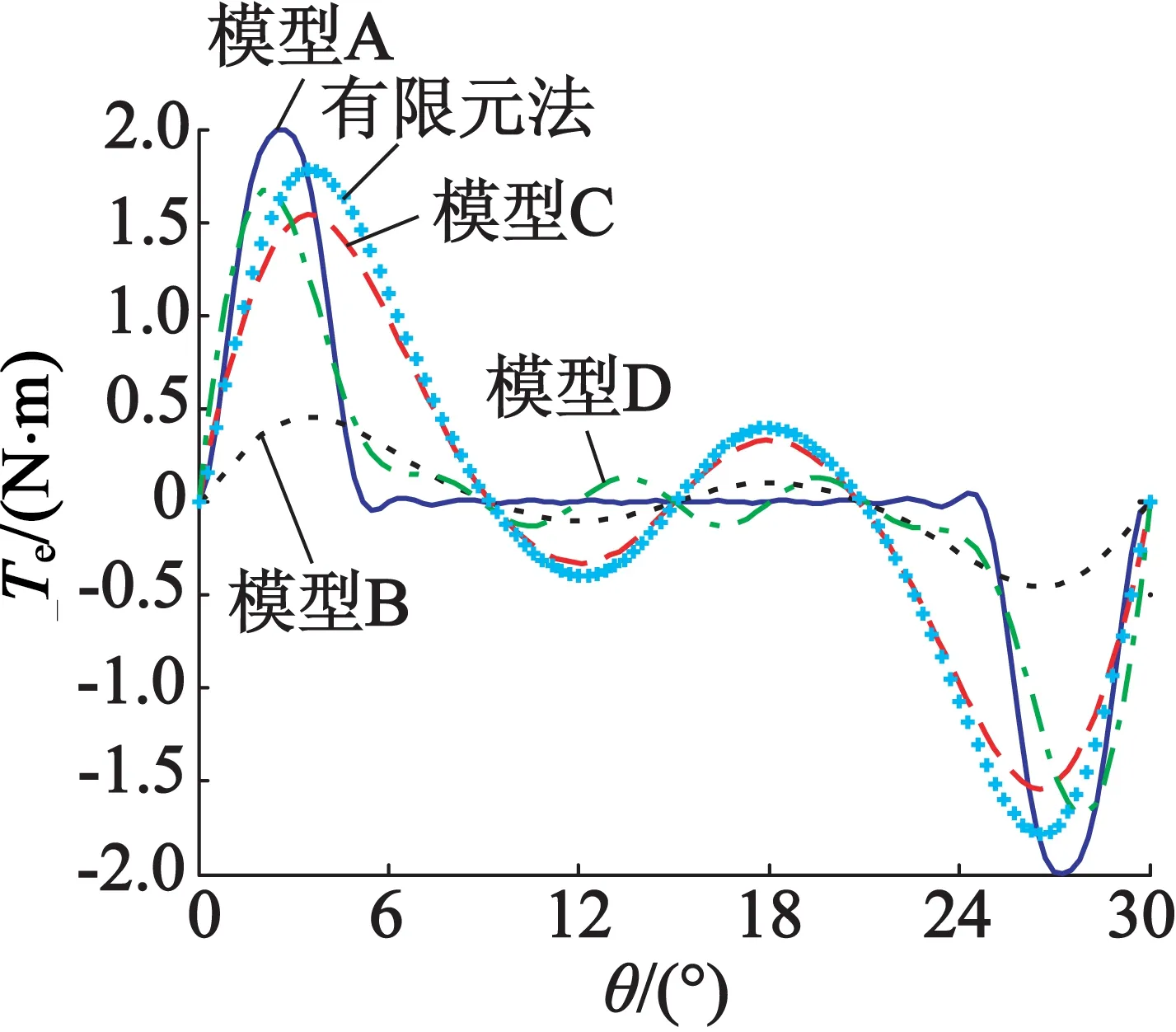
(a) αp=0.7

(b) αp=0.9

在上述模型中，用能量法的模型，在計算氣隙磁密或相對磁導時，取的位置是在定子的內表面。而利用麥克斯韋應力張量法的模型，在計算電機的氣隙磁密時，半徑取在氣隙的中間處。實際上，在氣隙的不同位置處，得到電機的氣隙磁密波形顯然不同，但是得到的齒槽轉矩并沒有區別。為此，取氣隙中的不同位置，即r分別為Rs-0.1g和Rs-0.9g，得到電機的徑向氣隙磁密波形如圖5所示。

再取氣隙中的不同位置，即r分別為Rs-0.1g，Rs-0.5g以及Rs-0.9g，得到電機的齒槽轉矩波形如圖6所示。從圖6中可以看出，3個波形完全一致。因此，驗證了齒槽轉矩與位置無關的正確性。

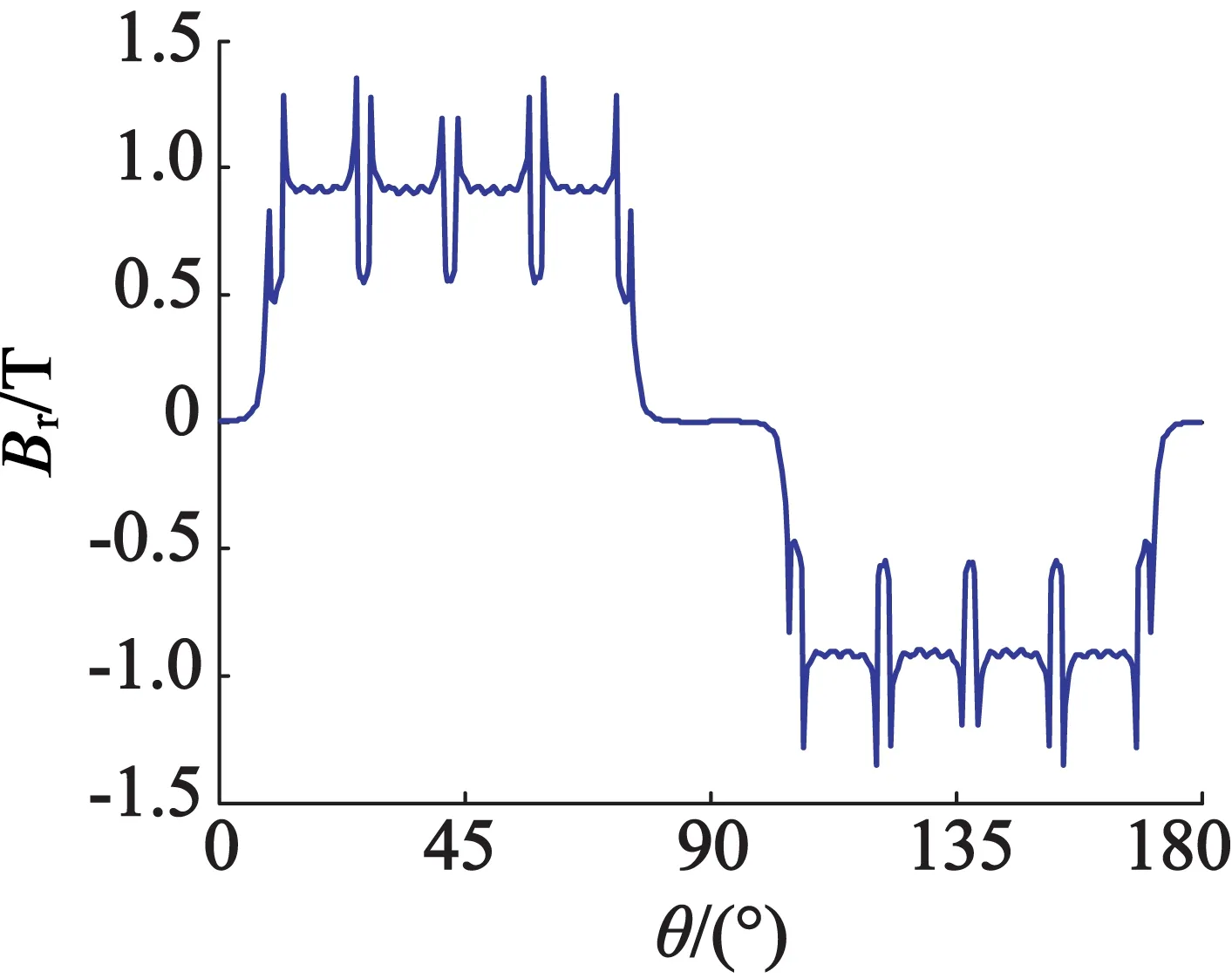
(a) r=Rs-0.1g

(b) r=Rs-0.9g

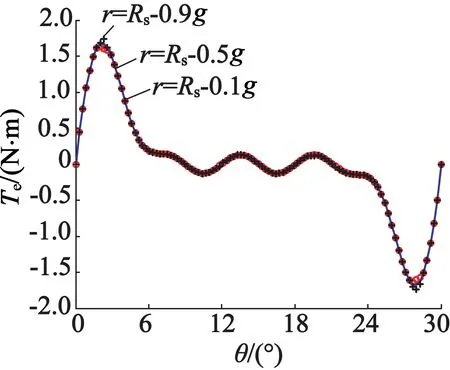
圖6 在氣隙中不同位置處的齒槽轉矩波形

3 結 語

本文比較分析了解析法計算表貼式永磁電機的齒槽轉矩的4種模型。分別是利用能量法的模型A、模型B和模型C以及利用麥克斯韋應力張量法的模型D。這4種模型都能計算表貼式永磁電機的齒槽轉矩。由于這些模型中考慮的因素不同，造成了齒槽轉矩的計算結果不同。與有限元法相比可知，模型C和模型D比模型A和模型B得到的齒槽轉矩結果更精確。相比于其它模型，模型D雖然計算量很大，但是精度較高。