基于剛體極限平衡法的不同透水條件岸坡穩定性研究

王俊萍 溫 霞 賈婷立

（內江職業技術學院 四川內江 641000）

1 理論分析

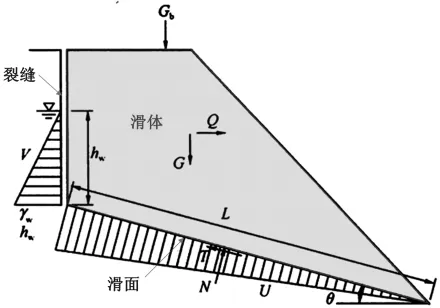
圖1 平面滑動面邊坡計算簡圖

邊坡穩定性分析之前，應根據巖土工程地質條件對邊坡的可能破壞方式及相應破壞方向、破壞范圍、影響范圍等作出初步判斷。判斷邊坡的可能破壞方式時應同時考慮到受巖土體強度控制的破壞和受結構面控制的破壞。計算沿結構面滑動的穩定性時，應根據結構面形態采用平面或折線形滑面，采用剛體極限平衡法計算邊坡抗滑穩定性。根據[4]穩定性系數的定義，穩定性系數等于抗滑力與滑動力的比值，具體計算公式如下：

T——滑體單位寬度重力及其他外力引起的下滑力（kN/m）；

R——滑體單位寬度重力及其他外力引起的抗滑力（kN/m）；

c——滑面的敬聚力（kPa）；

φ——滑面的內摩擦角（°）；

L——滑面長度（m）；

G——滑體單位寬度自重（kN/m）；

Gb——滑體單位寬度豎向附加荷載（kN/m），方向指向下方時取正值，指向上方時取負值；

θ——滑面傾角（°）；

U——滑面單位寬度總水壓力（kN/m）；

V——后緣陡傾裂除面上的單位寬度總水壓力（kN/m）；

Q——滑體單位寬度水平荷載（kN/m），方向指向坡外時取正值，指向坡內時取負值；

hw——后緣陡傾裂隙充水高度（m），根據裂隙情況及匯水條件確定。

穩定性分析過程中，上述公式同時考慮了滑面單位寬度總水壓力U、坡后緣裂隙水壓力V、水平荷載Q的影響，可根據具體工況條件，選擇所需要的公式類型來計算穩定性系數，分析邊坡的穩定性狀態。

2 模型計算

當坡體內、外由于降雨或水庫水位上漲及其綜合作用等因素，造成坡內、外存在靜水壓力，從而影響邊坡穩定性，同時坡體不同的透水條件，會影響坡內外靜水壓力的分布，進而影響邊坡穩定性，在穩定性計算過程中應予以考慮，主要討論如下幾種情形。

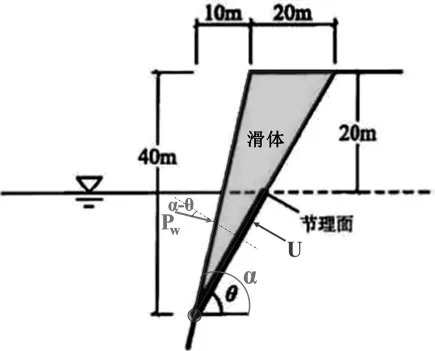
圖2 巖質邊坡的計算斷面

某很長的巖質邊坡的斷面形狀如圖2所示，巖體受一組走向與邊坡平行的節理面所控制，節理面的內摩擦角35°，內聚力為70kPa，巖體重度為23kN/m3。

2.1 工況一

不考慮水的作用，坡內、外均不存在靜水壓力，直接計算天然工況條件下邊坡沿節理面的抗滑穩定系數。

此時取沿長度方向1m長度來分析。

（1）滑體重：G=γV=23×0.5×20×40×1.0=9200kN

2.2 工況二

條件同2.1，但節理裂縫的一半充水，坡面外無水，坡底為隔水巖土層，計算邊坡沿節理面的抗滑穩定系數。此條件考慮降雨的計算模型。

取沿長度方向1m長度來分析，水位位于坡高中點高程，此時：

（1）滑體重：G=γV=23×0.5×20×40×1.0=9200kN

破裂角：θ＝53.1°；滑面長度：L=50m。

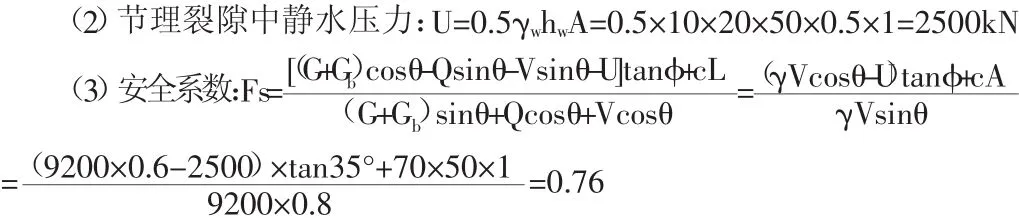
2.3 工況三

條件同2.1，但是不穩定巖體高度的一半被靜水淹沒〈節理縫隙的一半也充水〉，計算邊坡沿節理面的抗滑穩定系數。此條件考慮水庫水位上漲的計算模型，且坡面透水。

取沿長度方向1m長度來分析，不穩定巖體高度的一半被靜水淹沒，此時：

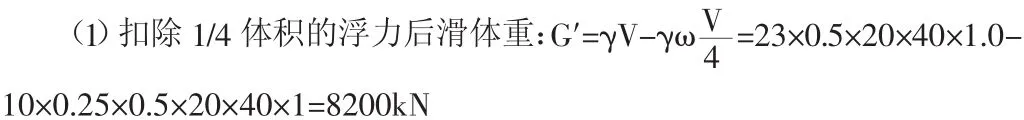
破裂角：θ＝53.1°；滑面長度：L=50m。

2.4 工況四

條件同2.1，但是節理縫隙無水，坡面外一半高度浸水，且坡面不透水，坡底為隔水土層，計算邊坡沿節理面的抗滑穩定系數。本條件考慮水庫水位上漲的計算模型，且坡面不透水。

取沿長度方向1m長度來分析，水位位于坡高中點高程，此時：

（1）坡外水壓力垂直作用于坡面，將在滑動面上產生法向和切向分力。

滑體重：G=γV=23×0.5×20×40×1.0=9200kN。

破裂角：θ＝53.1°；滑面長度：L=50m。

（2）坡面靜水壓力：Uw=0.5γwhwA=0.5×10×20×41.2×0.5×1=2060kN

坡面靜水壓力在滑面上的法向分力：Nw=Uwcos（α-θ）=2060×cos（76°-53.1°）=1898kN。

切向分力：Tw=Uwsin（α-θ）=2060×sin（76°-53.1°）=802kN。

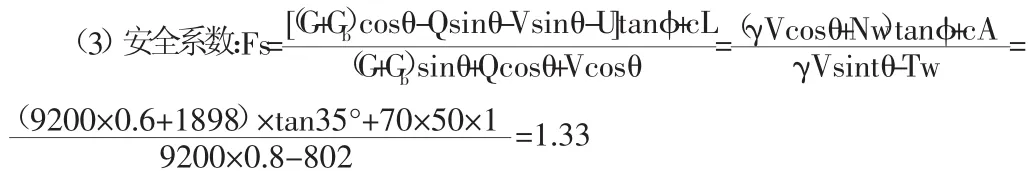
2.5 工況五

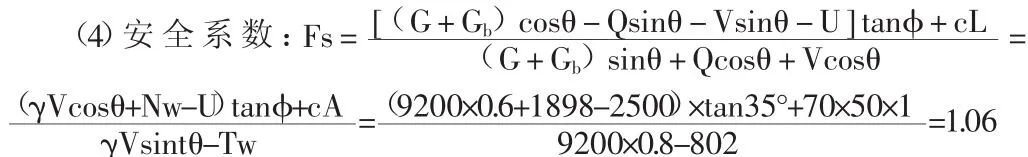
條件同2.1，但是節理縫隙有水，坡面外一半高度浸水，且壩坡面不透水，坡底為隔水土層，計算邊坡沿節理面的抗滑穩定系數。本條件考慮水庫水位上漲和降雨綜合作用的計算模型，且坡面不透水，降雨與水位上漲在坡內外高度一致。

取沿長度方向1m長度來分析，水位位于坡高中點高程，此時：

（1）坡外水壓力垂直作用于坡面，將在滑動面上產生法向和切向分力。

滑體重：G=γV=23×0.5×20×40×1.0=9200kN

破裂角：θ＝53.1°；滑面長度：L=50m

坡角：α＝76°；坡面長度：Lp=41.2m

（2）坡面靜水壓力：Uw=0.5γwhwA=0.5×10×20×41.2×0.5×1=2060kN

坡面靜水壓力在滑面上的法向分力：Nw=Uwcos（α-θ）=2060×cos（76°-53.1°=1898kN。

切向分力：Tw=Uwsin（α-θ）=2060×sin（76°-53.1°）=802kN

（3）節理裂隙中靜水壓力：U=0.5γwhwA=0.5×10×20×50×0.5×1=2500kN

將不同工況條件下邊坡穩定性系數結果匯總見表1和圖3，結合邊坡規范中穩定性狀態劃分標準及邊坡安全穩定性系數選取規定，選永久邊坡一般工況條件，邊坡工程安全等級為三級時的邊坡安全穩定性系數1.25，則不同工況下岸坡的穩定性狀態結果可見表1。

表1 不同工況穩定性系數匯總表

3 討論與結論

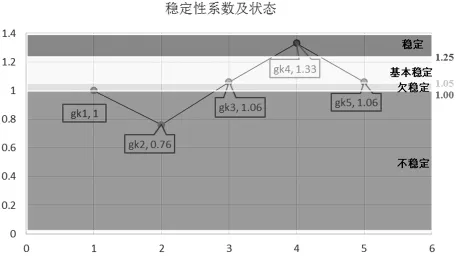
圖3 不同工況穩定性系數及狀態

本文模型計算是基于剛體極限平衡的平面滑移穩定性分析，且考慮了降雨和邊坡水位上漲及其綜合作用下的穩定性，取得了一定的有意義的結論，揭示了坡面作防滲后的蓄水引起反壓護坡與降雨誘發滑坡啟動的原因，坡體內部靜水壓力是滑坡啟動的初始動力；但是在分析過程中未考慮滲流作用引起動水壓力，如需考慮可在穩定性系數計算式中添加穩定滲流狀態下確定的坡體內滲透力，依據滲透力對不穩定滑體的抗力和下滑力貢獻度來分配其在穩定性系數計算公式的位置。

由于采用剛體極限平衡法計算的平面滑移穩定性，滑體視為剛體，不考慮剛體自身的變形和內部的破壞，故此結論主要適用于透水條件極差的受結構面控制的均一滑體結構，對于坡體內外透水的結構僅反映的某一靜態時刻的結果，并未考慮透水的動態過程。但作為傳統分析方法可通過穩定性系數確定的標準數值，結合規范中穩定性狀態與穩定性系數區間對應關系，來定量反映邊坡的穩定狀態。選取不同時刻的工況狀態進行靜力分析，可在一定程度上反映邊坡穩定性的動態發展過程。

本文通過剛體極限平衡的平面滑移穩定性模型計算，得到如下結論：

（1）通過分析可知天然工況下，岸坡滑體處于極限平衡狀態，穩定性系數為1.0。對比工況1和2可知降雨使得坡內節理裂隙存在一定深度的靜水壓力，滑動面法向力減小，從而使得抗滑穩定系數減小只0.76，系數折減了24%，表明降雨誘發滑體失穩影響大。此為降雨誘發滑坡失穩的基本力學原理。

（2）對比工況1和3可知，水位上漲，且岸坡坡面透水，滑體重γV減小，粘聚力c假定不變，抗滑穩定系數增加。但增加不大，僅增加了6%，由于c相對較小，對穩定系數的貢獻較小，故抗滑穩定系數增加量值不大。

（3）對比工況1和4可知，水位上漲，且岸坡坡面不透水。坡面外水壓力垂直作用于坡面，產生法向和切向分力，法向分力增加了抗滑力，切向分力減小了滑動力，從而使得抗滑穩定系數增加，穩定系數增加至1.33，系數增加了33%，邊坡反壓護坡的作用效果很顯著，僅考慮了力學平衡，未考慮水巖之間化學過程的離子交換（水巖作用機理）和物理過程的掏蝕等作用。對比3和4可知水位上漲對岸坡的穩定性均有一定提升，如要提升增大，需在坡表作防滲處理。對于坡體局部存在軟弱帶，水的弱化作用下造成力學強度降低，會引發新的不穩定滑體失穩，故本文假定滑體為均一的巖體。

（4）對比3和5可知，兩種工況的穩定性系數相等，工況5節理縫隙有水，坡面外一半高度浸水，且壩坡面不透水，坡底為隔水土層，本條件考慮水庫水位上漲和降雨綜合作用的計算模型，且坡面不透水，降雨與水位上漲在坡內外高度一致。工況3為不穩定巖體高度的一半被靜水淹沒〈節理縫隙的一半也充水〉，此條件考慮水庫水位上漲的計算模型，且坡面透水。可知此類情形下，滑體0.25倍的體積在水下，受到水的浮力作用，故工況5降雨與水位上漲在坡內外高度一致時，才會和工況3的穩定狀態一致，如果降雨強度小，裂縫中水位遠小于庫區水位上漲，此時穩定性系數大于1.06，無限接近1.33，即工況4情形；如果降雨強度大，裂縫中水位遠大于庫區水位上漲，此時穩定性系數小于1.06，無限接近0.76，即工況 2。

（5）縱觀多種工況下邊坡的穩定性系數數值可知，對于極限狀態的滑體，降雨和水庫水位抬升均會導致穩定性系數數值減小，進而誘發滑體失穩。如在坡體表面作一定防滲處理后可以提高岸坡的穩定性，為滑坡治理提供理論參考。坡表防滲與排水降低后緣裂縫和滑面上的水位，可有效提高岸坡穩定性。

本文為內江職業技術學院2018年度院級教科研課題“不同透水條件公路邊坡穩定性研究”研究成果（NZ2018C11）。