雙體工程輔助船波浪載荷

王福新, 任苗苗, 劉益清

(1.武漢東喻專利代理事務所， 湖北 武漢 430074； 2.華中科技大學 專利中心， 湖北 武漢 430074；3.武漢理工大學 交通學院， 湖北 武漢 430063)

0 引 言

雙體船由于載荷狀態復雜，因此其在波浪中的載荷計算[1-4]比較困難。國內外學者基于不同的假定和計算模型，各自提出有關雙體船載荷計算的近似方法有：美國的Scott方法、Disenbacher方法，蘇聯的伏羅洛夫方法，日本的Unzawa和Shimizu方法；國內專家提出的相關簡化算法(如孔炳慶方法)[5]，毛筱菲[6]提出利用模型試驗方法確定作用在雙體船連接橋結構上的波浪誘導載荷，汪學良等[7]對雙體船波浪載荷測試技術進行系統研究。

目前，雙體船包括普通雙體船、小水線面雙體船以及后來發展起來的穿浪雙體船。針對高速雙體船，CCS《小水線面雙體船指南》(2005)及《海上高速船入級與建造規范》(2012)對其波浪載荷計算有詳細的規定；針對內河雙體船，CCS《鋼質內河船舶建造規范》(2009)對其載荷計算有詳細的規定；而對于海上航行(主要是沿海航區)的中低速雙體船，CCS《國內航行海船建造規范》(2012)及其2013、2014年修改通報雖沒有給出具體的規范公式，但指出應基于波浪載荷直接計算或試驗得到。因此，本文采用直接計算方法對雙體工程輔助船所承受的波浪載荷進行預報。

1 計算模型的建立

預報雙體工程輔助船波浪載荷需要建立水動力模型和質量模型。

1.1 船型資料

雙體工程輔助船主要用于沿海航區為一些工程船供應貨物。船舶的主要尺度及參數如表1所示。

表1 船舶的主要尺度及參數

1.2 水動力模型

對雙體工程輔助船進行波浪載荷計算時，采用的是基于三維繞射-輻射及Morison理論為基礎的WADAM程序[8]，因此需建立水動力面元模型。HydroD模塊的水動力模型如圖1所示。

圖1 HydroD模塊的水動力模型

1.3 質量模型

質量模型對船舶波浪載荷計算的精度至關重要。質量模型和實船的質量重心差別越小，波浪載荷計算精度就越高。為此，需要實際統計全船各部分質量并按靜力等效原則得到全船質量沿船長方向的分布，滿載出港工況下的質量模型如圖2所示。

圖2 滿載工況質量模型

2 水動力分析

波浪引起的船體載荷是隨機統計量，在校核雙體工程輔助船結構強度時，需要根據沿海航區的波浪統計資料(P-M波浪譜和中國沿海波浪散布圖)，將其置于相應的波浪環境中，計算其在波浪上的運動和誘導載荷[9]。

2.1 浪向頻率和浪向

為充分研究雙體工程輔助船的水動力性能，計算時：選取頻率在0.20～1.80 rad/s范圍，步長為0.05 rad/s，共計32個遭遇頻率；選取13個浪向角，即在0°～180°之間，每間隔15°選取1個，等概率分布。沿船長方向共取9個剖面計算縱向波浪載荷；沿船寬方向共取5個剖面計算橫向波浪載荷。計算航速取零,即Fn=0。

2.2 傳遞函數結果及分析

本文應用WADAM模塊計算雙體船的運動和各主要載荷的傳遞函數，并應用POSTRESP[8]模塊顯示傳遞函數的結果。

(1) 滿載出港工況下的船體垂蕩運動在13個浪向上的傳遞函數如圖3所示。

圖3 滿載出港工況垂蕩運動傳遞函數

(2) 滿載出港工況下船體橫向載荷傳遞函數如圖4所示。

(3) 滿載出港工況下船體縱向載荷傳遞函數如圖5所示。

圖4 滿載出港工況橫向載荷傳遞函數

為便于分析及后文計算規則波參數，表2總結了各響應對應的最不利波浪和傳遞函數的最大幅值。

圖5 滿載出港工況縱向載荷傳遞函數

表2 傳遞函數

雙體工程輔助船在波浪中航行，由于波浪的擾動會產生搖蕩運動，其中對船體結構安全影響最大的是垂蕩、縱搖和橫搖3個運動分量。通過對3種工況下傳遞函數曲線和最不利傳遞函數最大幅值進行分析，可知該雙體船的運動響應有以下幾個特點。

(1) 雙體工程輔助船的垂蕩運動響應在橫浪時達到最大，縱搖運動響應從橫浪到頂浪逐漸增大，橫搖運動響應在橫浪時達到最大。垂蕩、縱搖和橫搖運動的傳遞函數最大響應幅值大多出現在頻率為1.25～1.45 rad/s(波長大約在29.32～39.45 m)范圍，即當船舶遭遇的波長與船長相近時，運動響應幅值最大。

(2) 通過比較分析，橫垂向彎矩響應幅值大多在橫浪附近時達到最大，并且滿載出港工況下的響應幅值最大、壓載到港工況下的響應幅值最小，響應峰值發生在波長船長比為0.84左右時。縱搖有關扭矩在艏(艉)斜浪時達到最大，滿載出港工況下的響應幅值最大,壓載到港和滿載出港結冰工況下的響應幅值比較接近。

(3) 縱向扭矩在艏斜浪附近時響應幅值達到最大，壓載到港工況下的響應幅值最大，滿載出港結冰工況下的響應幅值最小。由此表明，雙體工程輔助船在壓載航行時的縱向扭轉較為嚴重。

2.3 波浪載荷的長期預報

根據規范要求及研究需要，該船在不規則波浪上的運動和波浪載荷響應及其短長期預報計算采用P-M波浪譜。

(1)

SESAM/POSTRESP模塊提供了2種波浪統計資料：世界范圍波浪散布圖(DNV-WW)和北大西洋波浪散布圖(DNV-NA)，分別用于疲勞強度分析(FLS)和極限強度分析(ULS)[10]，它們并不適用于中國沿海航行船舶波浪載荷的長期預報。因此，本文在計算時以中國沿海波浪散布圖[11]作為長期預報的參考海況，在POSTRESP模塊中建立新的波浪統計資料。

分別對截面104縱向扭矩、截面203橫垂向彎矩和縱搖有關扭矩進行長期預報。為更加直觀地表述長期預報的結果，POSTRESP模塊將長期預報結果以圖片的形式顯示出來。限于篇幅，此處僅列出滿載裝載工況下各主要載荷參數的長期預報曲線、各主要載荷參數的長期預報值在超越概率下和不同浪向上的分布，如圖6、圖7所示。

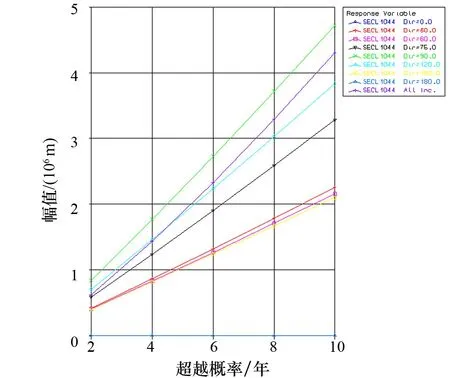
圖6 LC1截面104縱向扭矩長期預報曲線

為便于分析，本文總結了滿載工況下各主要控制載荷二十年一遇、二十五年一遇、三十年一遇及一百年一遇預報極值及其在超越概率下的預報值，如表3所示。

圖7 LC1縱向扭矩長期預報值在不同浪向上的分布

表3 LC1給定超越概率下的長期預報值 106 N·m

從長期預報的結果可以總結出以下結論：

(1) 從表3可以看出，主要控制載荷參數二十年、二十五年及三十年一遇的預報極值在數值上很接近，結合規范要求，本文選取二十年一遇(超越概率為10-8)的預報極值來推導設計波參數。

(2) 3種工況下截面203垂向彎矩的長期預報值在不同浪向上的分布表現為雙峰形式，極大值集中出現在連接橋與片體連接處，該處的結構形式在結構設計中要引起足夠的重視。

2.4 設計波參數的確定

(1) 設計波波幅計算式為

(2)

式中：aW為設計波波幅；Aj為主要載荷參數的極值；Lj為主要載荷參數的長期預報值，概率水平取10-8(代表設計壽命至少為20年)；j為主要載荷控制參數編號。

(2) 設計波波長計算式為

(3)

式中：λ為設計波的波長，m；g為重力加速度；ωa為主要載荷控制參數極值對應的波浪頻率，rad/s。

(3) 設計波的頻率等于主要載荷控制參數極值對應的波浪頻率ωa。

(4) 設計波的浪向等于主要載荷控制參數極值對應的浪向角β。

(5) 設計波的相位等于主要載荷控制參數極值對應的相位角εj。

根據以上設計波參數計算公式，確定滿載工況對應的設計波參數，如表4所示。

表4 LC1設計波參數

3 結論與建議

綜合分析，從雙體工程輔助船結構設計、駕駛及其理論研究等角度提出了建議與對策。

(1) 通過比較分析可知：雙體工程輔助船的垂蕩運動響應在橫浪時達到最大,縱搖運動響應從橫浪到頂浪逐漸增大,橫搖運動響應在橫浪時達到最大。通過長期預報可知，滿載出港工況下截面203垂向彎矩的長期預報值在不同浪向上的分布表現為雙峰形式，極大值集中出現在連接橋與片體連接處，該處的結構形式在結構設計中要予以加強，比如加強結構尺寸或單獨設置加強結構，并對該處的結構受力情況進行校核，確保其結構強度滿足要求。

(2) 橫垂向彎矩響應幅值大多在橫浪附近時達到最大，并且滿載出港工況下的響應幅值最大、壓載到港工況下的響應幅值最小，響應峰值發生在波長船長比為0.84左右時。縱搖有關扭矩在艏(艉)斜浪時達到最大，滿載出港工況下的響應幅值最大、壓載到港和滿載出港結冰工況下的響應幅值比較接近。建議在駕駛過程中，尤其是滿載出港工況下注意盡量避免雙體工程輔助船斜浪航行，以減小船舶在艏(艉)斜浪時的縱搖扭矩，保證船體結構強度不受損壞。

(3) 縱向扭矩在艏斜浪附近時響應幅值達到最大，壓載到港工況下的響應幅值最大，滿載出港結冰工況下的響應幅值最小。由此表明，雙體工程輔助船在壓載航行時的縱向扭轉較為嚴重。因此，建議在船舶駕駛過程中避免艏斜浪航行以減小船體結構的縱向扭矩，避免船體縱向結構尤其是連接處結構受到損壞。