基于尾渦強度的無人機與民機縱向安全間隔評估研究*

楊新湦，任 治

(中國民航大學 空中交通管理學院，天津 300300)

0 引言

無人機(Unmanned Aerial Vehicle, UAV)技術的快速發展與廣泛應用在全球掀起了一股熱潮，但近期無人機入侵機場凈空、威脅民航客機安全等“黑飛”事件讓無人機的科學管控成為民航安全運行領域亟待解決的難題。從安全科學角度看，無人機在非隔離空域與民航客機應該保持多少安全距離(即安全間隔)是首要、核心的問題，該間隔的評估問題也是監管機構與無人機使用者關注的焦點。民機飛行過程產生的尾渦(Wake Vortex)會導致尾隨運行的其他航空器發生失速、滾轉等不穩定現象，而無人機體型小、重量輕，一旦闖入尾渦流場，在誘導速度影響下失控后將發生解體，運動的機體碎片在尾渦場中極易被吸入發動機或與民機發生碰撞，嚴重危及航行安全。因此，考慮尾渦運動理論，建立無人機與民機安全間隔評估的有效模型是有必要的。

目前，國內外對于無人機安全間隔的評估研究還處于概念階段，尚未形成成熟的評估理論和方法。在民航領域，安全間隔評估始于20世紀60年代的Reich模型[1]，2008年徐肖豪等[2]首次系統地對國內外主要的碰撞風險模型進行比較，分析出飛行間隔安全性評估的關鍵問題是模型限制、管制意圖和安全評價，認為隨著通信、導航及監視(Communication Navigation and Surveillance, CNS)性能的完善, 未來間隔評估研究的趨勢是基于CNS性能建立碰撞風險模型。近年來，隨著各類航行新概念的提出，特別是基于性能導航(Performance Based Navigation, PBN)和4D航跡方面相關研究的突破，使得安全間隔研究涌現出很多新的成果：張兆寧等[3]在Reich模型基礎上，考慮CNS性能推導出平行航路縱向重疊概率的計算公式，建立了CNS性能平行航路縱向間隔評估模型；黃寶軍[4]在傳統碰撞風險模型中引入CNS性能和管制認知過程，認為CNS性能中導航性能對位置誤差影響最大；張兆寧等[5]將CNS性能誤差用概率表示為以理論位置向外輻射，提出CNS性能誤差具有高斯白噪聲特性；翟文鵬等[6]采用飛行流模擬的方法，對ADS-B監視技術下的PBN平行航路進行安全間隔評估，實現了飛行流整體運行下的航路安全風險評估。在尾流及尾渦研究方面，French[7]對后機在前機尾渦流場內，誘導下洗速度作用下的滾轉、傾斜、失速現象進行了研究；Sarpkaya[8]提出采用渦消散率(eddy dissipation rate)代替湍動能(turbulent kinetic energy)來描述尾渦的消散，以研究尾渦強度與其消散規律；魏志強等[9]采用鏡像渦模擬尾渦，研究尾渦地面效應與消散機理，并將模擬結果與大渦模擬及激光雷達實測數據進行對比；周彬等[10]借助保守被動模型，基于升力線理論建立尾流快速建模方法，實現對不同時刻尾流影響區域的可視化仿真。

上述研究使得民航客機安全間隔理論日趨成熟，本文將結合民航客機與無人機各自的運行特性，在民機CNS性能和無人機GPS運行環境下，基于尾渦流場強度消散的Crow不穩定性理論[11]改進碰撞模型，針對民機起飛后初始爬升剖面的運行實際，建立給定TLS下無人機尾隨民機運動時所需的縱向安全間隔評估模型。為驗證模型有效性，針對重、中、輕3類機型尾渦強度消散差異性，通過Matlab求解相應縱向安全間隔值，計算結果經分析后證明該模型具有較強的科學性和適用性。

1 民機尾渦流場消散模型

飛行過程中，上下翼面的壓力差不僅提供飛機所需的升力，還產生由下翼面繞過翼尖向上翼面流動的氣流，形成2個反向旋轉的翼尖渦，即尾渦，如圖1所示[12]。尾渦影響范圍和強度是安全間隔評估模型中改進碰撞模板(collision slab)的重要依據。相較于航路巡航階段，進離場和起降階段尾渦影響相對較大，同時由于飛行高度低，也是無人機與民機產生沖突最多、最危險的階段。尾渦流場的運動與消散過程主要分為近場渦和遠場渦2個主要階段，其消散率(eddy dissipation rate)符合Crow不穩定性理論，近場渦是尾渦形成和演化階段，在其影響范圍內流場強度變化速率較低，而遠場渦消散快，流場強度隨時間推移迅速減弱。

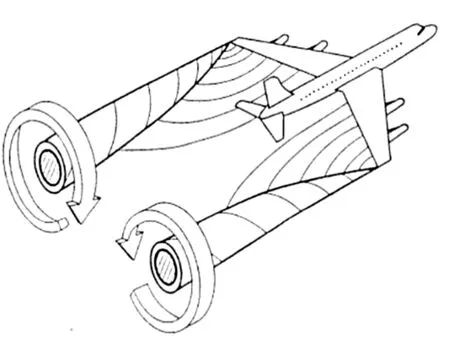
圖1 飛機尾渦的形成Fig.1 Sketch of aircraft wake vortex

Crow不穩定性由Crow在1974年提出[13]，該理論認為尾渦消散的原因是強度相同的尾渦間的誘導作用導致在擴散運動中2個渦連接起來，形成1個新的尾渦流場。尾渦強度在連接之后迅速減小，且一定尺度的大氣湍流在尾渦縱向距離上所造成的不穩定的波動加速了這種連接消散的形成。Crow不穩定性雖未考慮地面效應影響，但是本文研究的民機爬升階段地面效應逐漸減弱，可不予考慮，因此，仍然選用該理論研究尾渦消散率。

由于近場渦階段尾渦下沉趨勢不明顯，且流場強度較大，該階段進入尾跡區的無人機在尾渦影響下動能激增，位置與速度方向難以預測，極有可能射向民機，造成難以預料的損失；而遠場渦下沉趨勢明顯，無人機進入該尾跡區后被迅速拋向地面，勢能減小，雖然也會失控，但是由于民機處于爬升階段，二者具有較大的相對速度和逐步拉大的垂直間隔，碰撞風險顯著降低。因此，本文只考慮近場渦強度消散對安全間隔評估的影響。

1.1 近場渦消散模型

近場渦的消散過程中主要用渦環量(vortex circulation)來描述流場強度，此外，渦距s(vortex separation)、渦核半徑r(vortex core radius)也是描述尾渦的重要參數[14-15]。飛機的最大起飛重量、速度以及氣象等因素也會影響尾渦的形成與消散，式(1)為尾渦參數向量。進離場階段尾渦的數據可以通過機場激光雷達實際測得，也可利用大渦模擬進行仿真分析。在對數據精度要求不高的情況下，采用式(2)可以快速得到較為精確的渦環量估計值。

(1)

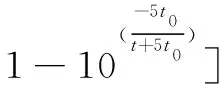
(2)

式中：λ為飛機翼展,m；MTOW為最大起飛重量，kg；g為重力加速度，m/s2；ρ為大氣密度，kg/m3；V為對應MTOW下的最大飛行速度，m/s；Γ(t)為時刻t的渦環量，m2/s；Γ0為初始渦環量，m2/s；ω0為尾渦參考下沉速度，m/s；t0為尾渦基準時間，s。

1.2 近場渦尾跡區域

近場渦強度變化較小，該階段渦環量僅下降10%左右，且上文已分析表明遠場渦影響可不予考慮。可據此特性，利用式(2)近似表示出近場渦階段持續時間tc，如式(3)所示。該時段內民機與渦核運動的相對距離即可近似表示為近場渦尾跡影響區域Sw，如式(4)所示，v為民機與渦核相對速度。

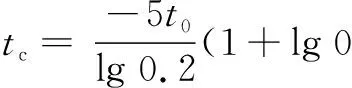
(3)

Sw=vtc

(4)

若已知尾渦參數及民機飛行數據，依式(4)快速確定近場渦尾跡影響區域Sw，該近似值將用于縱向間隔評估模型，對傳統Reich碰撞模板進行改進。

2 縱向間隔評估模型

航空器間需要保持的安全間隔通常分為縱向間隔、側向間隔和垂直間隔3種，其中縱向間隔根據航空器運動方向可細分為對頭和尾隨2種情形。在民機起飛后初始爬升階段，發動機采用全發最大爬升推力離場，爬升梯度大，高度上升快，而無人機爬升能力有限，若無人機與其保持較大縱向間隔對頭運行，可以通過爬升迅速增大垂直間隔解除沖突；若無人機尾隨民機運行，則正好落入民機近場渦尾跡影響區，經流場能量傳遞后失去控制危及民機航行安全。因此，本文主要針對無人機尾隨民機情形下的縱向安全間隔建立評估模型。

2.1 改進的Reich模型碰撞模板

碰撞模板的劃設是建立Reich碰撞風險模型的前提，其原理是將2架沖突航空器的外部保護區構型疊加到其中1架航空器上，從而將問題抽象為1架航空器作為質點入侵運動中的碰撞模板，以簡化碰撞風險計算分析過程。傳統的Reich模型基于平行航路碰撞風險，其碰撞模板是1個以2架沖突航空器機身長之和、翼展之和、機身高之和分別為長、寬、高的長方體，此外還衍生出圓柱體、球體等碰撞模板，用于交叉航路及VOR導航模式下的碰撞風險模型。無人機尾隨民機情形可抽象為平行航路下的兩機縱向間隔評估，故選用長方體碰撞模板，同時考慮近場渦尾跡區影響，改進Reich模型碰撞模板以便于建立間隔評估模型。

民機外部保護區構型需要針對近場渦影響進行改進，而近場渦的影響應該從縱向、側向和垂直3個方向分別考慮，本文只建立縱向間隔模型，故只考慮近場渦尾跡區對縱向區域的影響，忽略渦核外擴和下沉在側向和垂直方向的影響。圖2為尾渦影響區域俯視圖，Sw為1.2節計算得到的近場渦尾跡影響區域，為便于計算，近似以機翼中點所在徑向剖面為起始端，且該剖面距機頭約0.5倍的機身長(λx)。

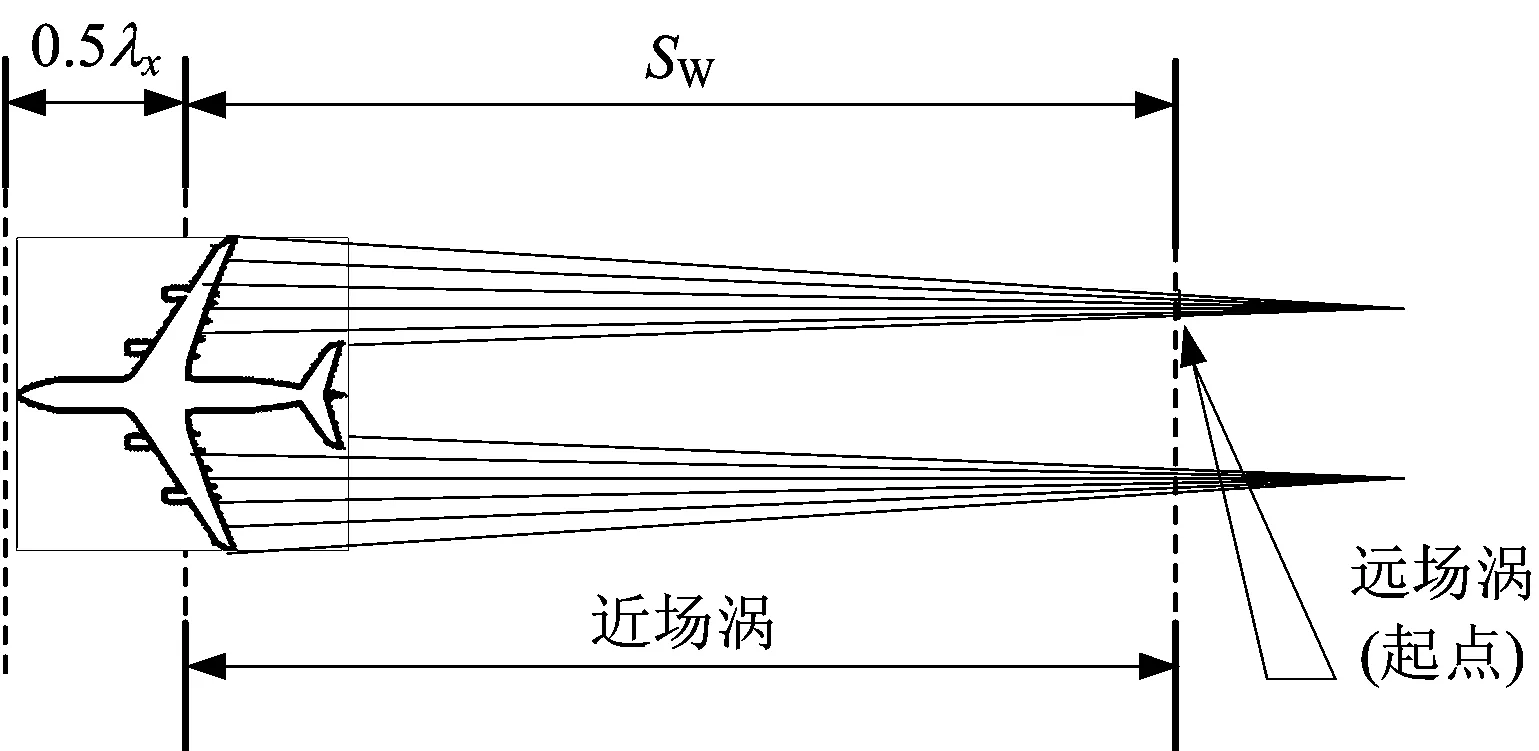
圖2 尾渦影響區域俯視圖Fig.2 Top view of wake vortex affected area

無人機外部保護區構型較為簡單，常見多旋翼無人機外部構型凸連線呈正方形或長方形，記其機身長和機身寬的最大值為λu。將民機與無人機外部保護區構型疊加，得到改進的Reich模型碰撞模板，其縱向幾何尺寸記為為Sx，見式(5)：

Sx=0.5λx+Sw+λu

(5)

2.2 位置誤差影響下的縱向間隔評估模型

除了尾渦的影響，位置誤差的存也導致航空器運行需要保持較大的安全間隔。民機位置誤差通常由通信、導航與監視性能(Communication, Navigation and Surveillance, CNS)、航空氣象、飛行技術誤差(Flight Technical Error, FTE)等因素導致，在目前技術環境下，CNS性能對位置誤差的影響最大。無人機室外運行主要依靠GPS導航，因此導航精度也是導致無人機產生位置誤差的重要因素，但是無人機導航系統抗干擾能力較弱，極易受地形、電磁、通訊鏈路等因素的影響，商業產品多采用RTK差分技術，配合慣性導航、圖像定位以及離線訓練提高其定位導航精度，因此，以GPS系統標稱的定位精度進行評估實際上得到的間隔值會偏小。研究表明，CNS性能與GPS系統的誤差均可利用正態分布來表示[16-20]。

無人機尾隨民機運行過程中，兩機距離是分析其碰撞風險的主要指標。假定民機從機場起飛后，無人機尾隨民機飛行，在較短的時間間隔內，可近似看作處于同一高度，將縱向上民機位置誤差記為X1，無人機位置誤差記為X2；兩機初始縱向距離記為d，m；實際距離記為D，m，則有如下分布：

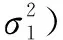
(6)

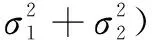
(7)

CNS性能導致的民機位置誤差的標準差σ1可表示為如下形式：

(8)

GPS系統導致的無人機標稱位置誤差的標準差σ2可表示為如下形式：

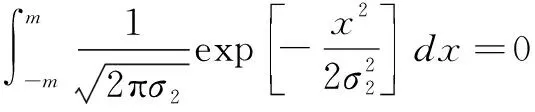
(9)

式中：n1，n2，n3分別為民機RNP，RCP，RSP性能參數；m為無人機GPS系統標稱精度參數；V為民機飛行速度，m/s。

若將無人機GPS系統修正標準差記為σxiu，則兩機初始距離為d時的碰撞風險(Collision Risk，CR)可記為：

CR=2P(|D-d|≤Sx)=

(10)

給定安全目標水平TLS可依式(10)得到需要保持的兩機初始距離，該距離稱為滿足相應TLS水平下的縱向最小安全間隔dTLS。但是，直接給定TLS反解dTLS過程較為復雜，目前通用的解法是變換兩機初始距離，利用Matlab通過逐步搜索算法逼近TLS水平值。

3 評估分析算例

航空器類型、飛行速度等都會影響近場渦尾跡區的大小，進而影響碰撞模板的大小。本文選取重、中、輕3類常見民機與四旋翼無人機作為算例評估對象，在不同的飛行速度以及導航設備性能環境下利用Matlab建立評估模型進行求解。算例所需各項參數見表1。

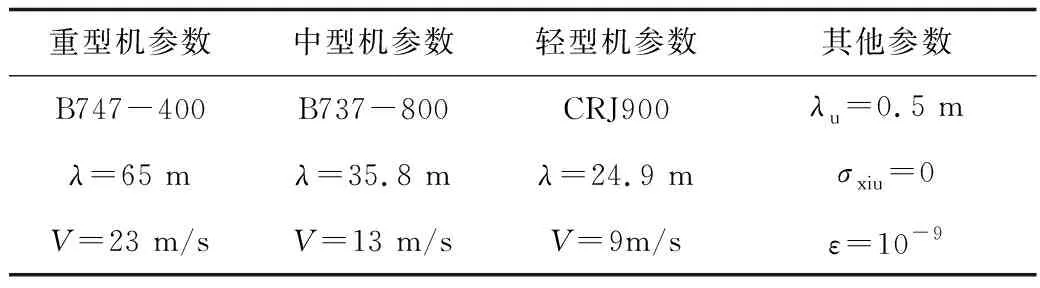
表1 算例參數Table 1 Parameters of the sample

評估得到的縱向間隔值除可用于非隔離空域內無人機與民機混合運行時的間隔保持參考外，還可為機場無人機禁飛電子圍欄的劃設提供理論支持。RNP1性能環境最接近機場周圍性能環境，為得到RNP1環境下安全間隔值浮動區間，由重中輕3種機型，飛行速度為180～220 kt，GPS20和GPS50 2種類型隨機組合100個計算方案，求解得到結果如圖3所示，可以發現安全間隔值在6.6～7.3 km之間浮動。該間隔區間可作為跑道端線凈空范圍劃設參考,現行機場凈空保護區由機場每一條跑道中心線10 km，跑道端線20 km的范圍構成，若僅考慮CNS/GPS及尾渦流場影響，跑道端線凈空范圍可依據7.3 km實際影響區域進行精細化劃設。

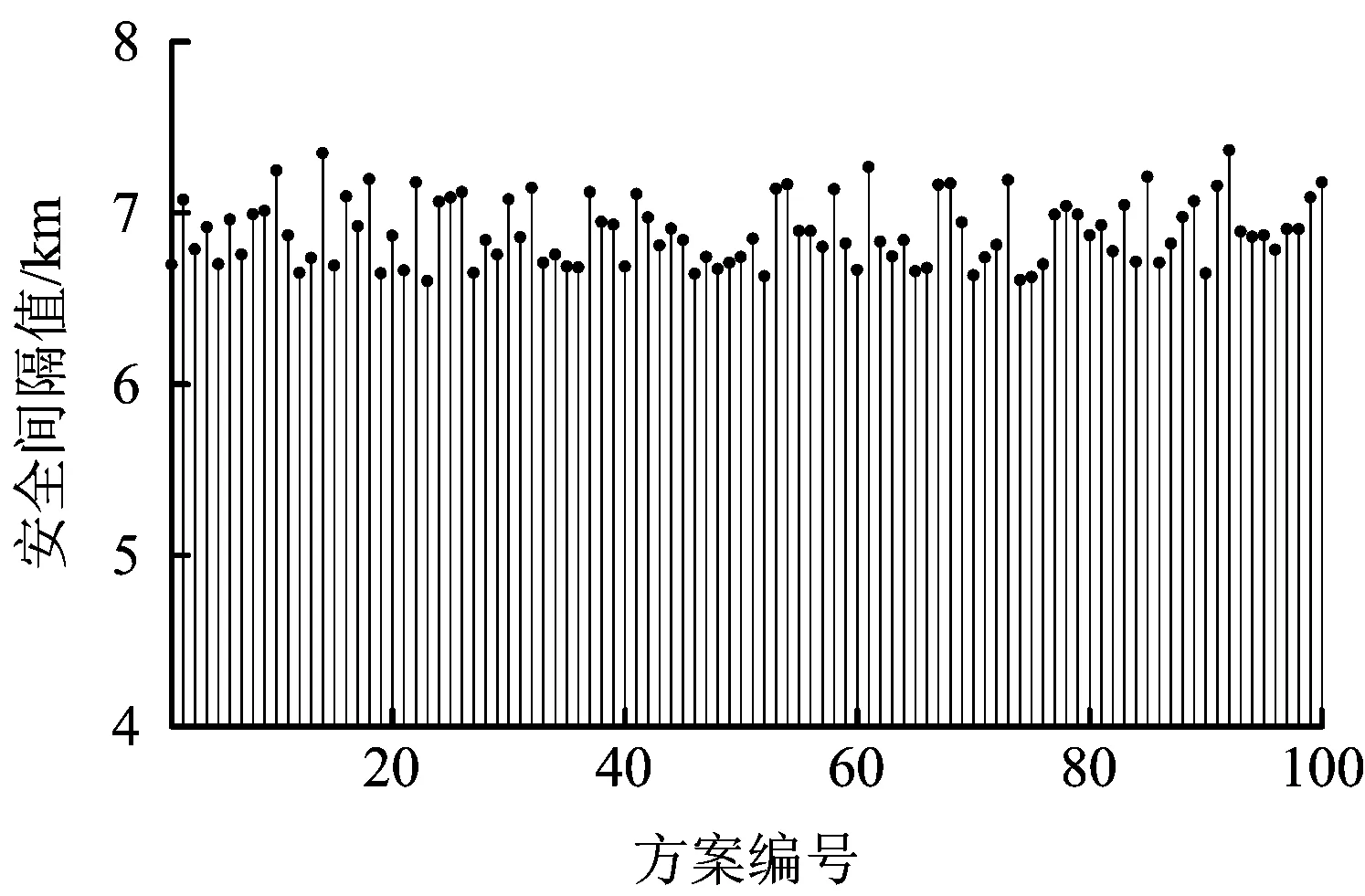
圖3 RNP1環境下隨機方案對比Fig.3 Contrast of 100 random scenarios on RNP1

3.1 導航性能對安全間隔的影響

本文涉及的導航性能由民機RNP與無人機GPS構成。無人機導航精度GPS50，民機選用B737-800，速度200 kt時的算例顯示，RNP性能對安全間隔影響很大，RNP1性能環境下間隔約為6.803 km，RNP4為22.736 km，RNP10為55.623 km。隨著民機導航精度的下降，所需安全間隔不斷增大，變化趨勢如圖4所示，而無人機GPS對安全間隔影響較小，B737-800/RNP4/200 kt算例結果可知，GPS20與GPS50安全間隔值分別為22.653 km和22.772 km，如圖5所示，相差119 m，均可記為23 km。

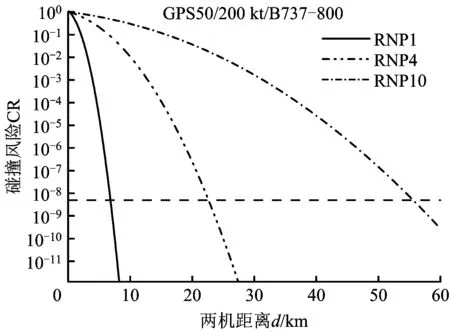
圖4 民機導航性能與安全間隔變化關系Fig.4 Effect of RNP on the separation

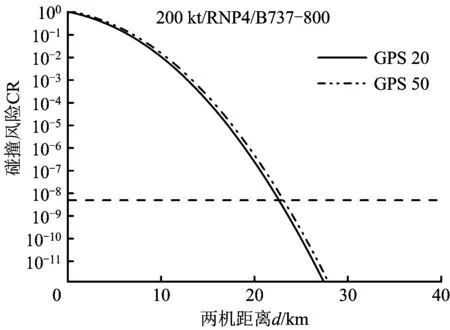
圖5 無人機導航性能與安全間隔變化關系Fig.5 Effect of GPS on the separation

3.2 尾渦參數對安全間隔的影響

根據上文尾渦消散模型可知，在機型(考慮翼展、翼型參數)和速度不同時，近場渦跡影響區及持續時間不同，影響碰撞模板大小，使得安全間隔值發生相應變化。圖6為速度對間隔值的影響，可知速度越大，所需間隔越大。圖7為機型影響，同理，重型機(B747-400)尾跡區最大，所需間隔最大，中型機(737-800)與輕型機(CRJ900)所需間隔依次減小。總體來看，圖6線條較圖7稀疏，表明飛行速度對安全間隔的影響略大于機型。

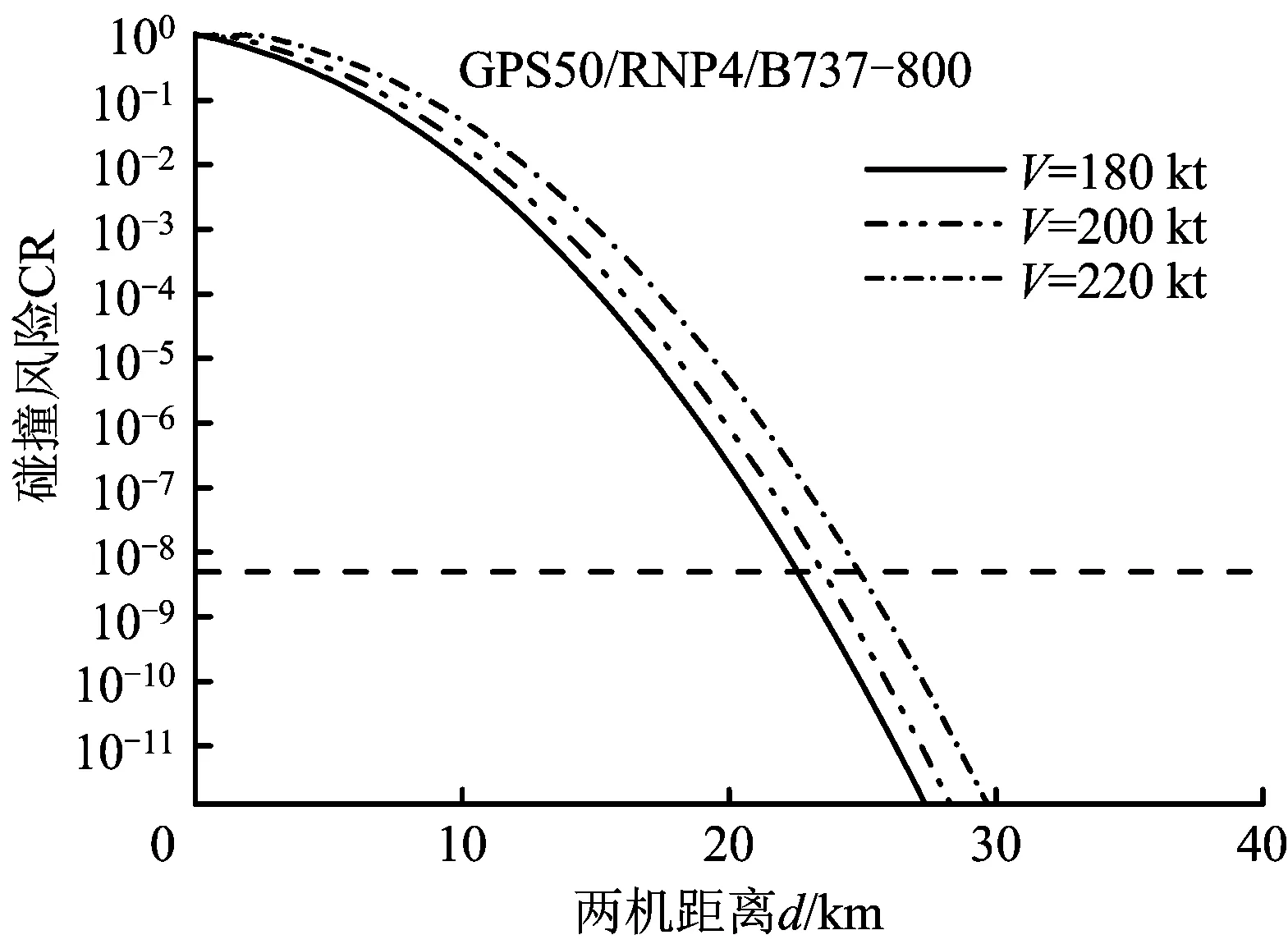
圖6 民機速度與安全間隔變化關系Fig.6 Effect of speed on the separation

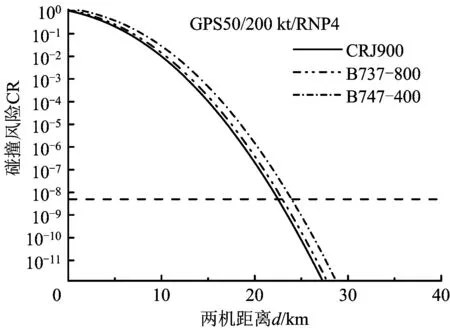
圖7 民機機型與安全間隔變化關系Fig.7 Effect of aircraft type on the separation

4 結論

1)無人機電子圍欄可考慮7.3 km實際影響區域在20 km現行標準下進行相應精細化設置。

2)航空器導航性能越差，所需間隔越大，且民機導航性能在安全間隔評估中的影響遠大于無人機。

3)速度大小和機型大小與安全間隔值呈正比關系，且速度影響略大于機型影響。

4)無人機與民機間隔還包括側向、垂直等多種類型間隔，以及發動機噴流、電磁干擾以及復雜氣象等多種影響因素對間隔的影響，而機場凈空保護區劃設還應考慮起落航線結構和障礙物限制面等因素，因此模型仍具有一定的局限性。